Linear Systems Flashcards
(26 cards)
What is the equation for a vertical line?
x=x Intercept
Example: x=3
What is the equation for a horizontal line?
y=y Intercept
Example: y=2
What is an Intercept?
Where a line segment crosses the x or y axis.

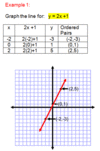
How do you use a table of values to determine all of the points in a line segment?
Step 1) Choose your X values
Step 2) Write out your equations to find Y and replace the x variables with the values you chose
Step 3) Write your x and y coordinate pair
How do you plot an equation in y=mx+b form?
Step 1) Plot the y-intercept (b)
Step 2) From the y-intercept, use rise/run to find another point
Example: y=2x+4
Plot (0,4)
Use rise/run to plot the next point
m= 2/1 (up 2 over 1)
How do you find the x and y intercepts of a line?
Example: y= x+6
Set the opposite intercept to zero and solve. Graph all found points.
X Intercept Y Intercept
y=0 x=0
y=x+6 y=x+6
0=x+6 y=0+6
-6=x y=6
(-6,0) (0,6)
What does slope measure?
Steepness, the greater the slope the steeper the line.
Example: y=-10x+3 is steeper than y=5x-7
What equation is used to find the slope of a line when given 2 points?
y2-y1
x2-x1
What equation is used to find the equation of a line when given slope and the y-intercept?
Substitute the slope and the y-intercept into y=mx+b
Example: Slope=7 and y-intercept= -3
y=mx+b
y=7x-3
What equation do you use to find the equation of a line when given slope and a point?
Substitute the slope and x and y points into y=mx+b, and solve for b (y-intercept)
Example: Slope= 3/4 Point= (-1,2)
y=mx+b
2=3/4 (-1) +b
2=-3/4+b
2/1+3/4=b
b= 8/4+ 3/4
b= 11/4
What is the slope of 2 Parallel lines?
The slopes are equal.

What is the slope of 2 Perpendicular lines?
They are the negative reciprocal of eachother (Flip the fraction)
Example: m= -1/2 and m=2/1
What does No Solution look like?
Slope is the same, y-intercept is different
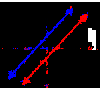
What does One Solution look like?
Slopes are different

What does Infinite Solutions look like?
Same slopes and same y-intercepts
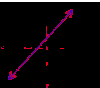
What does it mean to solve a linear system?
To find the point(s) of intersection of 2 equations
What are the 5 methods to solving a linear system?
1) Table of values method
2) x and y-intercept method
3) y=mx+b method
4) Substitution
5) Elimination
How do you check that your ordered pair is a solution to a linear system?
Substitute your ordered pair back into the equation. Both sides of the equation should be the same.

How do you find the point of intersection by Substitution?
Example: y=3x-1 and 2x-y=9
Step 1) Label Equations 1 and 2
(1) y=3x-1
(2) 2x-y=9
Step 2) Rearrange one of the equations to isolate for x or y
y=3x-1
Step 3) Substiture the expressions from step 2 into the other equation and solve
Sub 1 into 2
2x- (3x-1)=9
2x-3x+1=9
- x-9-1
- x/-1=8/-1
x= -8
Step 4) Substitute the value found in step 3 into one of the original equations to find the other variable
Sub x= -8 into (1)
y=3x-1
y=3(-8) -1
y=-25
Step 5) Write a conclusion
Therefore the point of intersection is (-8, -25)
* Refer to “Solving Linear Systems by Substitution Method” for more information
How do you find the point of intersection, by Elimination?
Example: x+3y=7 and x+y=3
Step 1) Label the equations 1 and 2
(1) x+3y=7
(2) x+y=3
Step 2) Multiply every term in one or both of the equations so that the variable you want to eliminate has the same or different coeffcient
x+y=3 → X -1 → -x-y= -3
Step 3) Add or subtract to eliminate one variable
0x+2y=4
Step 4) Solve for one variable
2y/2= 4/2
y=2
Step 5) Substitute the value found in step 4 into one of the original equations to find the the value of the other variable
Sub y=2 into (1)
x+3 (2) =7
x+6=7
x=7-6
x=1
Step 6) Write a Conclusion
Therefore the point of intersection is (1, -2)
*Refer to “Solving Liner Systems Using Elimination” for more information
What is a First Difference Column?
A column on your table of values that tells the dfference between one number to the next. This helps you to Determine if the graph is linear or non-linear
Example: from 3 to 5 the first difference is 2
What is a Second Difference Column?
A column on your table of values that tells the dfference between one number to the next, in the first difference column. This helps you to see if the graph is a parabola.
How can you tell if a graph is linear or not by a table of values, and first difference column?
If the x and y columns increse or decrese by the same amount then the graph is linear.
How can you tell if a graph is a parabola based on a table of values and a second difference column?
If the second difference columns increses or decreses by the same amount then the graph is a parabola.


