Lesson 3: Portfolio Theory Flashcards
(10 cards)
Glen is considering two portfolios: 1) Portfolio A with a return of 14 percent and a standard deviation of 14 percent and 2) Portfolio B with a return of 4 percent and a standard deviation of 7 percent. Assuming the correlation between A and B is 0.0 and Glen invests 70 percent in A and 30 percent in B, what range of returns should this portfolio produce 95 percent of the time?
A) Between 1% and 21%
B) Between -9% and 31%
C) Between -1% and 21%
D) Between -19% and 41%
The correct answer is (B).
Standard deviation:
=SQRT[(0.7² x 14² ) + (0.3² x 7² ) + 0]
=SQRT[(0.49 x 196) + (.09 x 49)]
=SQRT[96.04 + 4.41]
=SQRT[100.45]
=10.02% or about 10%
Expected return = (0.7 × 14%) + (0.3 × 4%) = 11%
As noted in Chapter 2, the 95 percent confidence interval equals two standard deviations from the mean. Therefore the range -9 percent to 31 percent is the correct answer.
The expected market return is 12 percent, and the risk-free rate of return is 3 percent. Using the CAPM formula, what is the expected return for a portfolio that has a standard deviation of 18 percent and a beta of 1.3?
A) 12.0%
B) 13.8%
C) 14.7%
D) 15.6%
The correct answer is (C).
CAPM = Rf + β(Rm – Rf)
CAPM = 3% + 1.3 × (12% − 3%) = 14.7%
Consider the graph with the security market line (SML). Which of the following statements is correct?
A) The betas for Portfolios A, B, and C are all the same as they are all on the SML.
B) The return for Portfolio C will be equal to the market premium minus the risk-free rate.
C) If the return for the market was 12 percent and the risk-free rate was 3 percent, then A’s expected return could not equal 15 percent.
D) Portfolio A is the riskiest portfolio.
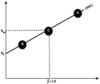
The correct answer is (D).
The x-axis in this graph is risk. Portfolio A is furthest along the x-axis and therefore the riskiest. Option (A) is incorrect as the beta for C is the market beta of 1.0, while the beta for B is less than 1.0 and the beta for A is more than 1.0. Option (B) is incorrect because the return for C will equal the return for the market, which is also the market premium plus the risk-free rate. Option (C) is incorrect as A’s return could equal 15 percent if the beta for A were 1.3333.
Toby recently graduated from college with a degree in finance. He enjoys stock analysis and is eager to get started with investing in the market. He has approximately $30,000 of student loan debt at an average interest rate of 4.2 percent, and the $300 monthly payment is easily manageable even at the starting salary for a new college graduate. Although Toby does not currently have any savings, he has asked a financial planner to assist him with opening a brokerage account where he can begin buying stocks to save toward his goal of buying a condo in the next 7 to 8 years. Which of the following is true?
A) Toby’s willingness (tolerance) to take on risk is greater than his ability (capacity) to take on risk, so the planner should encourage him to begin investing toward his goal by purchasing stocks in the brokerage account.
B) Toby’s ability (capacity) to take on risk is greater than his willingness (tolerance) to take on risk, so the planner should encourage him to begin investing toward his goal by purchasing stocks in the brokerage account.
C) Toby’s willingness (tolerance) to take on risk is greater than his ability (capacity) to take on risk, so the planner should encourage him to accumulate emergency funds prior to purchasing stocks in a brokerage account to save for the goal.
D) Toby’s ability (capacity) to take on risk is greater than his willingness (tolerance) to take on risk, so the planner should encourage him to accumulate emergency funds prior to purchasing stocks in the brokerage account to save for the goal.
The correct answer is (C).
Risk capacity is a measurement of the amount of risk a client can afford to take on. Risk tolerance is the amount of risk a client is willing to take on. When risk capacity and risk tolerance are not in alignment, the more conservative of the two should determine the planning recommendations. In this case, Toby has the tolerance to take on risk; however, since he has not yet accumulated any emergency funds, he lacks the capacity to absorb losses. Therefore, he should build his emergency funds first and then begin investing for other goals.
Jayden invested $3,000 in CJD stock, $3,000 in JCD stock, and $3,000 in JFD stock. CJD, JCD, and JFD have expected returns of 6 percent, 7 percent, and 10 percent, respectively. What is the weighted expected return for Jayden’s portfolio?
A) 7.67%
B) 7.00%
C) 6.76%
D) 4.20%
The correct answer is (A).
Because the amount invested in each stock is the same, the weighted average equals the simple average of the returns, or 7.67%.
Assume Marcie adds to her portfolio Security Y, which is less than perfectly positively correlated with the portfolio. Security Y has the same standard deviation as the portfolio. What will happen to the standard deviation of the portfolio after she adds Security Y?
A) It will remain the same.
B) It will decrease.
C) It will increase.
D) It may increase or decrease, depending on the weightings of the portfolio holdings.
The correct answer is (B).
The portfolio standard deviation should decrease because the added security is not perfectly correlated with the portfolio. For example: The portfolio standard deviation is 20 percent, and Security Y’s standard deviation is 20 percent. The correlation between the portfolio and Security Y equals 0.95. With a weight of 95 percent for the portfolio and 5 percent for Security Y, the combined standard deviation equals 19.95 percent.
Nyssa is considering two portfolios: 1) Portfolio A with a return of 11 percent and a standard deviation of 16 percent and 2) Portfolio B with a return of 6 percent and a standard deviation of 10 percent. Assuming the correlation between A and B is 0.0, which of the following is the most efficient portfolio?
A) 10% A / 90% B
B) 20% A / 80% B
C) 30% A / 70% B
D) All three combinations of A and B are equally efficient.
The correct answer is (C).
The expected return is the weighted average return. The standard deviation of each combination is found using the following formula:
Option (A) return and standard deviation = 6.5% and 9.14%, respectively. Option (B) return and standard deviation = 7.0% and 8.62%, respectively. Option (C) return and standard deviation = 7.5% and 8.49%, respectively. The most efficient (highest return for given level of risk) is Option (C). Options (A) and (B) are inefficient.
Evan has a portfolio of mutual funds, A, B, and C. She has 50 percent in A, 40 percent in B, and 10 percent in C. What is the expected return for the portfolio if the relative expected returns for A, B, and C are 10 percent, 8 percent, and 14 percent?
A) 11.50%
B) 10.67%
C) 9.60%
D) 9.35%
The correct answer is (C).
The weighted average expected return equals (0.5 × 10%) + (0.4 × 8%) + (0.1 × 14%) = 9.6%.
Consider the chart with the seven portfolios and the efficient frontier. Which of the following portfolios is the most efficient in terms of risk and return?
A) Portfolio A
B) Portfolio D
C) Portfolio E
D) Portfolio F
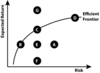
The correct answer is (B).
Portfolios B, C, and D are all efficient.
Portfolios A, E, and F are all inefficient as there are other attainable portfolios with a higher return for the given level of risk.
Portfolio G is unattainable.
The expected market return is 12 percent, and the risk-free rate of return is 3 percent. Using the CAPM formula, what is the expected return for a portfolio that has a standard deviation of 18 percent and a beta of 1.3?
A) 12.0%
B) 13.8%
C) 14.7%
D) 15.6%
The correct answer is (C).
CAPM = Rf + β(Rm – Rf)
CAPM = 3% + 1.3 × (12% − 3%) = 14.7%


