Lecture Two Flashcards
What is the relationship between frequency and wave length? (Expressed in a formula).
vλ = c Where V is velocity. λ is wave length. C is the speed of light. Also note that Hz or s^-1 is frequency.
What did Max Planck explain?
He explained that:
- The wave nature of light does not correctly explain the distribution of wavelengths emitted by a glowing object.
- He assumed that energy comes in packets called quanta.
How did Einstein use Planck’s explanation to explain the photoelectric effect?
He concluded that ‘photons’ have energy proportional to frequency.
E = hv, where h is Planck’s constant, 6.63 * 10 ^34 J’s.
- Photon: particle representing a quantum of light or other electromagnetic radiation.
- Photoelectric effect: is the observation that many metals emit electrons when light shines upon them.
What did Einstein suggest about the relationship between frequency of light waves and the ejection of electrons?
- He suggested that only after exceeding a certain frequency can light enable the ejection of electrons from a metal surface.
- Proved that light has properties of quanta, not just waves.
How was Nils Bohr about to explain atomic emissions?
By assuming that:
- Electrons in a certain atom can only occupy certain orbits corresponding to certain energies.
- Energy is only absorbed or emitted in such a way as to move an electron from one ‘allowed’ energy state to another.
- The corresponding energy is then calculated using the relation: E = hv <– The Einstein relationship.
What equations can be used to calculate λ and v?
What did Louis de Broglie propose?
He proposed that if light can have material properties, then matter should exhibit wave-like properties.
De Broglie stated that a moving particle has a wave length given by:
λ = h/p where p = mv (p is momentum).
Note that for very light things, λ is significant.
But marcroscoping objects, λ is far too small to be determined.
What was the Schrodinger wave equation?
- A new ‘quantum mechanics’ is concieved by Erwin Schrodinger to describe microscopic objects such as the electrons in an atom.
- This mathematical treatement incorperates both the wave and particle nature of matter.
- The main point is that Ψ can only be used to make statements as to the probability of locating the electron.
- Ψ is the Greek letter psi which means wave function.
What are the simbols/equations for probability density? And what is probability density?
Ψ^2 and R(r)^2
The probability density describes the probability of finding an electron at a paint in space (from Ψ^2) with respect to the distance, r, from the nucleus.
What is the radical distribution function?
4πr^2R(r)^2 - aka, electron density.
- This function considers the probability of finding an electron (from Ψ^2), but this time within a spherical shell a distance of r from the nucleus.
- Since the volume of these shells increases as r increases, the function increases from zero thought a maximum before tending to zero again.
What are the quantum numbers and what are their characteristics?
Show how the quantum numbers represent the unique solutions to the Schrodinger equation.
Describe the characteristics of the quantum number, l.
We use a series of letters to labele the l values.
E.g. when n = 2, l = 1, it is a 2p orbital.
What is an atomic orbital?
- A solution to the schrodinger equation with quantum bumber n, l and ml (big m, subscript l).
Note: an orbital as a mathematical function, bot a region of space
- An orbital can exist all over space.
- As on gets further away from the nucleus, the probability of finding and electron gets smaller. Thus, the shape of an orbital is usually described by where the electron is likely to be found 95% of the time.
Describe the characteristics of the s orbital.
Spherical in shape.
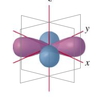
Describe the characteristics of the p orbitals.
- Dumberll shape.
- Can have three orientations along the x, y and z axis.
- These are called p subscript x, p subscript y and p subscript z.
Describe the characteristics of the d orbitals.
- Five orientations.
What are nodal planes?
- Represents a plane in space about which the wave function for a particular orbital has a zero probability amplitude.
- P orbitals have a single notal plane and d orbitals have two.
Draw a radial distribution function.
Describe penetration and shielding.
- The 2s orbital penetrates closer to the nucleus in comparison to the 2p orbital.
- An electron occupying the 2s orbital is said to shield an electron occupying the 2p orbital.
- The result is that the 2s orbital is lower in energy (more stable) than the 2p orbital.
Shielding: Electrons in an atom or ion are attracted to the positive nucleus by electromagnetic forces of attraction. The attractive fource experience by the outer shell electrons will be lessened by the shielding effect of the inner electrons.
