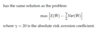Lecture 2 Flashcards
Let’s assume the price of the risk free asset is p. What is the return R
R = 1/p
When risk averse: The expected utility from buying a risky asset with the same expected payoff as the riskless asset is … than the utility from buying the riskless asset. A. Lower B. Equal C. Higher
Lower
What is the Certainty equivalent
The certainty equivalent CE(x) is the certain payoff that gives a utility equal to the expected utility from investing in the risky asset. By risk-aversion it is lower than the expected payoff of the risky asset, which is the payoff of the riskless one
Assume a function g() that is defined for two values x and y, x < y. The function is called convex if…
E serves as a replacement for lambda and lies between 0 and 1 g(Ex + (1 - E)y) < Eg(x) + (1 - E)g(y)
The more concave the VNM curve the more risk…
averse
An agent is risk averse if he demands a … risk compensation
Positive
An agent is risk averse IFF his utility function u is… An agent is risk taker IFF his utility function u is… An agent if risk neutral IFF his utility function u is…
Concave Convex Linear
How is the absolute risk aversion is defined
-U’‘(W) / U’(W)
What is (if nonzero), the reciprocal of the ARA used for…
Risk tolerance
On what is the WTP dependent using Absolute Risk-aversion
The willingness to accept this opportunity should be related to the risky amount, x, and his level of current wealth, W
In what sense is the relative risk aversion different to the absolute risk aversion
the amount at risk is a proportion of the agent’s wealth
What is needed for no arbitrage
Positive state prices
How are risk neutral probabilities created
By multiplying and dividing the RHS of the p=Xq with the summation of all state prices. This results in a state price of = q_s / [sum^S_1 q_s] This is nothing else than rescaled state prices
How are risk-neutral probabilities also called
Martingale probabilities
What are the (second version) two fundamental theorems of finance
Theorem I: Security prices exclude arbitrage IFF there exist strictly positive risk-neutral probabilities Theorem II: Security prices exclude strong arbitrage IFF there exist positive risk-neutral probabilities
What is the ‘General’ Fundamental Theorem of Finance
If there exists an equilibrium –> No arbitrage translates to existence of strictly positive risk neutral probabilities
Why is it called risk neutral valuation
This is due to the fact that he discounts the expected value of the payoffs with the risk-free rate, so he does not account for any risk-premium in the discount rate However, risk is captured into the risk-neutral probabilities Risk-neutral probabilities are nothing more than rescaled state prices, thus using them to price securities implies an underlying replicating strategy and hedging of excess risk
What is the definition of a Martingale
We say that a sequence (…xt, xt+1, …) of random variables (e.g. asset prices in different time periods) all defined on the same probability space (omega, mu), satisfies the martingale property if for every s and t with 0 <= s <= t it holds that E_{mu}(x_t | …, x_s) = x_s Essentially, the martingale property ensures that in a ”neutral” world, knowledge of the past will be of no use in predicting future. Only the information available today is relevant to make a prediction on future prices.
What is the martingale property
Essentially, the martingale property ensures that in a ”neutral” world, knowledge of the past will be of no use in predicting future. Only the information available today is relevant to make a prediction on future prices.
What does the martingale property imply
No arbitrage We silently assume that the prices of the existing assets are no arbitrage prices, thus we find the martingale (risk-neutral) probabilities and price the redundant asset
What is dynamic completion
we manage to complete the markets through retrading at the second node For dynamic completion of markets the number of securities traded must be no less than the maximum number of branches emanating from each node on the event tree
What is the key of the arbitrage pricing theory
The key to the APT lies in the identification of risk factors in the economy that capture the risk-premium for all securities in the economy APT replaces the concept of the state of nature with the hypothesis that there exists a stable set of factors that are essential and exhaustive determinants of all asset returns
Is the APT an equilibrium model
Arbitrage Pricing Theory (APT) provides an expression for deriving the risk-adjusted return via arbitrage arguments without considering explicitly an equilibrium model
What is the difference of the APT with a equilibrium model
The difference from equilibrium models is that the prices of fundamental securities are not derived from primitives but will be deduced empirically from observed asset returns without attempting to explain them
In what way does the CAPM relate to the APT
It is obvious that if we assume that the movement (return) of the aggregate stock index is the only factor affecting asset returns, then we get CAPM as a single factor APT model Nevertheless, we have to point out that CAPM suggests that the market portfolio is the only factor as an equilibrium result starting from fundamentals and under certain assumptions APT says nothing about which factor which should use or more importantly how many
To what does that simplify
This is a CARA utility function
