Lec 5- IV infusion

Question 1

IV bolus / infusion

Answer 1

• IV bolus dose
  
  • When repeated doses are required or when you need to maintain drug concentrations in the patients, it’s not a very convenient approach
  • Lots of sub-therapeutic time, small amount of therapeutic time
• IV infusion
  
  • Used within hospitals to provide a constant level of therapy to an individual
  • Allows control and maintenance of plasma concentrations and is a precise and controlled systems
  • Drug infusion can be stopped if there are adverse problems

Question 2

STEADY STATE ACCUMULATION

Answer 2

• IV infusions balance the INFUSION RATE (going in) with the CLEARANCE of the drug (going out)
• When this is the balance you reach steady plasma concentrations and this is called steady state

Question 3

IV infusion- background

Answer 3

• Our goal: to achieve a STEADY STATE concentration
• How long: 4-5 half-lives to reach STEADY STATE for every drug
• NB- Although counterintuitive, the half-life here refers to the elimination half-life
• NB-To reaches SS you need to infuse the drug for 4-5 half-lives to reach SS. The half-life is a function of each drug to the infusion time varies for each drug

Question 4

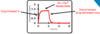
IV infusion

Answer 4

• Assume you have started the infusion and what to know the concentration at ANY point during the infusion
• You would have a Css and you should know some information about the elimination (k) of your drug
• We can use the following equation to follow what is happening to the drug DURING the infusion

Question 5

What type of drugs do you think are REQUIRED to be given by infusion?

Answer 5

• General anaesthetics
• Insulin pump (diabetic)
• Pain relieve- morphine infusion
• Narrow TI drugs (phenytoin, warfarin)
• Chemotherapy
• Antibiotics

Question 6

Case study 1: Steady state concentrations

Answer 6

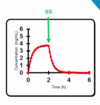
1. If the infusion rate and dose are the same as before, why has the Css (steady state concentration) increased?
   
   • Infusion rate- easy to manipulate
   • CL of the drug- difficult to manipulate- in this example there is a change in elimination
     
     • Time for drug to reach 0 is longer
     • 2. Can you estimate the half-life of this drug without doing any difficult maths?
   • 2 hours to reach SS, it takes 4-5 half-lives to reach SS, therefore, we can estimate 0.4-0.5 Hrs

Question 7

Case study 2: loading doses

Answer 7

• In many clinical situations, we require rapid clinical onset
• In these cases we often LOAD the patient with a high dose of the drug, to begin with- this is called the LOADING DOSE
• This approach pre-loads the patients with the clinically active dose
• If we gave an IV dose only, is this effective?
  
  • By pre-loading with a loading dose following by the maintenance (IV infusion) we achieve the profile above

Question 8

Case study 2

Steady-state concentrations

Answer 8

• What are your thoughts on this therapy
  
  • Assume the target concentration is 6ng/mL
• This is poor because you need to infuse for 18 hrs and you still haven’t reached therapeutic window, so doesn’t have much effect
  
  • This is caused by the fact the drug has a long half life

Question 9

If you know the target Css if 6-10 ng/mL, how would you work out an appropriate loading dose

Answer 9

• The loading dose is an IV-bolus dose. We can USE
  
  • Css = LD/Vd
• It can also be calculated by looking at
  
  • LD = R_<em>inf</em> / k_el
• The choice depends on which type of information you have availability in the clinical situation

Question 10

Case study 3: post infusion

Answer 10

• The graph opposite is a computer-generated profile where the red line is made up of hundreds of data points which represent hundreds of blood samples in one patient over the 24 hours
• This is not reflective of the clinical environment
• In some cases, we only have a few blood samples from a patient and may wish to calculate important PK of the drug

Question 11

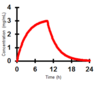
How can we work out the half-life of the drug in this patient

(Assume we didn’t know that 3 hours was Css)

Answer 11

• When we STOP the infusion it is the same as when we give a patient and IV-bolus dose at the exact moment
• The infusion is giving drug into the venous circulation and when we stop the infusion the only thing controlling the drug is it’s loss from the body

Question 12

Case study 3: Post infusion

We can use the first order equation

Answer 12

• C_t=C₀e^-kt
• And assume C₀ is actually Css
• You can then treat calculate the slope of an LN vs time
• OR Semi-log vs time graph to determine t_1/2
• OR this can be done visually
• Treat as an IV bolus dose example

Question 13

IV infusions: Changing parameter

Answer 13

• Mrs Smith has been admitted into a hospital ward
• She attends regular visits to be administered regular IV-infusions
• On the second visit to the clinical, she is now not clinically responding to her standard infusion setup
• Assuming that the rate of infusion and dose has not changed between the 2 visits, what has caused this change?
  
  • Concentration
  • CL
  • Half-life has changed

Question 14

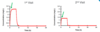
IV infusion: changing parameters

Answer 14

• Css has decreased
• If the infusion rate hasn’t changed then this is a result of an increase in the clearance
• It was discovered that this patient was suffering from a DDI which enhanced the clearance of the infused drug, perhaps from a newly prescribed medication
• Drug-drug interactions, liver, kidney
• Css = R_inf / CL

Question 15

Case study 5: full example

• A patient was given an IV infusion of drug X. The infusion was prepared by the addition of 5mL of a 25mg/mL solution of drug X to a 495mL of 0.9% w/v saline. The giving set was adjusted to deliver 40mL/h and this solution was infused for 10 hours
• Calculate the following parameter

Answer 15

• The dose the patient received
• The plasma concentration of the drug at the end of the infusion
• Elimination half-life
• Elimination rate constant
• Total body clearance of the drug
• A volume of distribution of the drug
• The steady state concentration that would have been achieved if the infusion had continued

Question 16

IV infusions

Answer 16

• 5mL of 25mg/mL solution = 5*25mg of drug =125mg of drug
• Total volume= 495 + 5 = 500mL
• Overall concentration = 125mg/500mL = 0.25mg/mL
• Delivered at 40mL per hour for 10 hours
• Total volume = 400mL
• Total dose = 400*0.25 = 100mg

Question 17

IV infusion

Calculated from graph, Estimated from data table

Answer 17

• Time is taken for 50% reductions in drug concentrations
• A more accurate way is to calculate the elimination rate constant (gradient) then convert to half-life

Question 18

IV infusion calculation: Elimination rate constant

Answer 18

• k = ln2/ t_1/2
• k= 0.17 h^-1
• Remember, units for a rate constant are time^-1 and units for half-life are time

Question 19

IV infusion calculation- Total body clearance of the drug

Answer 19

• The concentration did not reach steady state, therefore, we cannot use
• Css = R_inf/CL
• You need to use an alternative method
• The relevance of this term is the discussion more in later lectures

Question 20

IV infusions calculation

Area under the curve

Answer 20

• AUC- represents the residency of the drug in the body and is used to calculate the bioavailability
• It is also very useful in calculating the clearance of the drug, it is just the area under the curve
• AUC = Dose/ Clearance Units: mg.mL.hour
• By knowing the DOSE (see earlier) and AUC, we can calculate the CLEARANCE of the drug

Question 21

IV infusion calculations- Volume of distribution

Answer 21

• Cl = k.Vd
• As CL and k are known we can calculate Vd
• Vd= 20.7 / 0.17
• Vd= 121 Litres

Question 22

IV infusion calculation

The steady state concentration that would have been achieved if the infusion had continued

Answer 22

• C_t-inf = Css (1 - e^-kt)
• Select a random time point, I’ve chosen 1 hour
• Using data point t=1; C_t-inf = 0.077
• 0.077 = Css (1-e^-0.17*1)
• 0.077 = Css (1-0.84)
• Css = 0.077/(1-0.84)
• Css = 0.48 mg/L
• We have been give time and concentration and we have calculated k