Laplace Flashcards
What is the first shiftng theorem?
L{e-aty(t)}=y(s+a)
How would you use partial fractions with a denomenator of s(s2+4)?
(A/s)+((BS+c)/(s2+4))
With SHM, what is one of the definitions of ω?
ω=(k/m)0.5
What is the heaviside function?
sometimes denoted by u

What is the 2nd shifting theorem?
L{H(t-a) y(t-a)}=e-asy(s)
what is the delta function?
Known as an impulse function

What is the convolution theorem?
What is the transfer function?
G(s)=Y(s)/U(s)
Where G is the transfer function, Y the output and U the input.
Need to find Laplace transform Y(s) with an unknown input u(t) L{u(t)}=U(s)
What is the fourier series equation?

What are the equations for an and bn ?
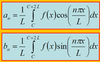
How do you find L for a fourier series?
period/2 =L
How is an odd and even function definded?
Even f(x)=f(-x)
Odd f(x)=-f(-x)
Average of an odd function=0
If a function is of the form f(x)=f(x+π), what does that mean for the harmonics?
Only even harmonics
f(x)=-f(x+π) has odd harmonics
What are the equations for the sum of a a fourier series?

How do you find the fourier transform of a function?

What is the quotient rule?

Integration by parts

How would you start this in partial fractions?


How would you find the laplace transform of t2cos(t)
Apply the laplace transform to cos(t) and then differentiate twice. Look at the formula at the bottom of the sheet.
What does a0/2 denonte?
The average of a function
If you did a fourier transform on an even fuction, how would this show in the result?
It would only contain cos functions
What is the fourier transform?

What is the average of an odd function?
0
what is the inverse fourier transform?
G(ω) is the fourier transform
f(t) is the inverse






