L3 - Intro to impacts (part 1)

Question 1

Simplified equations – coincident centre of masses

• Require knowledge of ________ ________
• Simple _____ between ______ approximation can be used.

(sketch a golf ball amd putter example)

Answer 1

underlying physics

impact, masses

Question 2

Simplified equations – coincident centre of masses

o If impact is to occur, V must be _______ than v and the relative velocity of approach is (__-__)

o Bodies are considered _______, therefore they will _______ after impact

o _’ must be greater than _’ and the relative velocity of separation will be (_’ – _’)

Write the Conservation of momentum equation for this system (where momentum in the system is the same before and after collision)

Answer 2

greater

(V - v)

elastic

separate

v , V

(v’ – V’)

*MV+mv=MV’+mv’ *(1)

Question 3

Simplified equations – coincident centre of masses

• Generally ,collision considered _____-______ (some energy lost, hysteresis loss – duo to deformation of bodies). This is dependent on _______ and __________. But they still _______from each other
• e, a coefficient of __________ can be included to account for this . e, is dependent on ________ properties of the bodies concerned.
• e, defined as a ratio of _______ (both ________ and _______). Write this eqaution.

Answer 3

visco-elastic

velocity

deformation

rebound

restitution

elastic

velocities

seperation , approach

e = (v’-V’ ) / (V - v) (2)

Question 4

** Simplified equations – coincident centre of masses**

Describe a perfectly elastic collision

Describe a perfectly plastic collision

Describe most practical cases

Answer 4

 Perfect elastic collision => rebound at same relative velocities at which they met => e =1

 Perfect plastic collision => no rebound at all => e=0

 Most practical cases lie somewhere between these two extremes

Question 5

Simplified equations – coincident centre of masses

Derive the velocities of after the collision.(v‘and V’)

(Hint) Use the momentum conservation and coefficient of restitution equations

Answer 5

Question 6

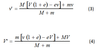
Simplified equations – coincident centre of masses

In this putter case , where mass m is stationary before impact, v = 0 , therefore, the equations reduce to:

Answer 6

Question 7

Simplified equations – coincident centre of masses

give 2 complex examples of these collisions within sport

Answer 7

 Golf club head and golf ball collision

 Snooker balls collisions