L3 Financial Options

Question 1

What is a Call Option?

Answer 1

A contract that gives the buyer the right, but not the obligation, to BUY the underlying security at a pre-specified price within a respecified period of time. Pre-spec also known as strike or exercise price.

Question 2

What is a Put Option?

Answer 2

A contract that gives the buyer the right, but not the obligation, to SELL the underlying security at a pre-specified price within a respecified period of time. Pre-spec also known as strike or exercise price.

Question 3

What is the different between European and American Options?

Answer 3

EU can only be exercised at the expiration date of the option, but American may be exercised at any time prior to expiration date of the option.

Question 4

What is the Strike/Exercise Price?

Answer 4

The price of the option @ the time of sale.

Question 5

What is the difference between an option Buyer/Holder and an option Seller/Writer?

Answer 5

Buyer/Holder holds the right to exercise the option and has a LONG position in the contract. Seller/Writer sells/writes the option and has a SHORT position in the contract. Note: the buy has to pay them a premium as the long side has the option to exercise but short side has an obligation to fulfil the contract if it is exercised. i.e. insurance.

Question 6

What is “At the Money”?

Answer 6

=

exercise price = current stock price

Question 7

What is “In the Money”?

Answer 7

(+) An option whose value if immediately exercised would be POSITIVE.

Question 8

What is “Out of the Money”?

Answer 8

(-) An option whose value if immediately exercised would be NEGATIVE.

Question 9

Why do we use Options? (2)

Answer 9

Hedge: To reduce the risk by holding contracts or securities whose payoffs are (-)ively correlated with some rise exposure

Spectulate(Gamble): When investors use contracts or securities to place a bet on the direction in which they believe the market is likely to move.

Question 10

Buy Call Option Payoff Diagram

Answer 10

Question 11

Sell Call Option Payoff Diagram

Answer 11

Question 12

Call Option Profit to Buyer

Answer 12

Question 13

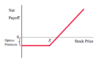
Call Option Profit to Seller

Answer 13

Question 14

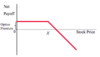
Long Put Option Payoff Diagram

Answer 14

Question 15

Short Put Option Payoff Diagram

Answer 15

Question 16

Put Option Profit to Buyer

Answer 16

Question 17

Put Option Profit to Seller

Answer 17

Question 18

What is a Put-Call Parity

Answer 18

A principal that defines the relationship between the $ of European put and call options of the same class (same underlying asset, strike price and expiration date. States that simultaneously holding a short European put and long European call of the same class will deliver the same return as holding one forward contract on the same underlying asset, with the same expiration and a forward price equal to the option’s strike price. If the prices of the put and call options diverge so that this relationship does not hold, an arbitrage opportunity exists, meaning that sophisticated traders can earn a theoretically risk-free profit. Such opportunities are uncommon and short-lived in liquid market

Question 19

Put-Call Parity Equation

Answer 19

C = P + S - PV(K)

Question 20

helloo

Put-Call Parity Equation w/ DIV

Answer 20

C = P + S - PV(K) - PV(DIV)

Question 21

What are the factors affecting Strike Price and Stock Price?

Answer 21

• value of a call option inc. as stock inc. All other things held constant.
• value of put option inc. as stock price dec. All other things held constant.

Question 22

The longer you hold an American Option, the more valueble the option. True/False? Is this the same with European.

Answer 22

This is true, an american option with a later exercise date cannot be worth less than an otherwise identical american option with an earlier date.

For European this is not tru as a later exercise date can be worth less than an otherwise identical European option with an earlier exercise date.

Note that American Options cannot be worth less than its European counterpart, the may have equal value.

Question 23

5 things.

What are some limitations (I guess) or features of options.

Answer 23

1. Put option cannot be worth more than its strike price
2. Call option cannot be worth more than its stock price
3. American Options cannot be worth less than its European counterpart, the may have equal value.
4. American option cannot be worth less than its intrinsic value
5. American option cannot have a negative time value i.e. diff bet option $ and intrinsic value.

Question 24

Does the value of an option generally increase with the volativity of the stock?

Answer 24

Yes :)

Question 25

Exercising Call Non-Dividend Options Early

Answer 25

American cannot be worth less than European options but MAY have equal value.

As dis(K) and P must be positive before expiration date, a europen call always has a postive value and as american option is work at least as much as the european THUS american option must also be positive before expiration.

Therefore the $ of any call option on a non-div paying stock always exceeds its intrinsic calue prior to expiration.

–> never optimal to exercise a call option on a non-div paying stock early (better off selling the option) BUT possibly optimal for a put.

Question 26

Exercising Put Non-Dividend Option Early

Answer 26

May be optimal to exercise a put option on a non-dividend paying stock early.

When a put option is sufficiently deep in the money “dis(k)” will be learge relative to the value of the call, and the time value of a european put option will be (-)ive.

Thus, the european put will sell for less than its intrinsic value.

Note that its amercan counter part cannot sell for less than its intrinsic value which implies that an american put can be worth more than its identical european option.

Question 27

Exercising Put Options with Dividend Paying Stocks Early

Answer 27

Written as…

C=S-K+dis(K)+P-PV(Div)

If Div is large enough, the time value of a european call option can be negative i.e. price could be less than its intrinsic value.

As an american option can never be worth less than its intrinsic value, the price of the american option can exceed the price of a european.

Question 28

What is the Black Scholes Model and the Formula (American Option)

Answer 28

Black-Scholes option pricing formula prices options on non-dividend paying stocks.

Question 29

Equation for calculating d1 and d2…

Answer 29

Question 30

What is the Black-Scholes Equation (European Option)

Answer 30

P = PV(K)[1 - Nd2] - S[1 - Nd1]