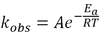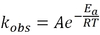Kinetics

Question 1

For the generic chemical reaction

aA + bB ⇒ cC + dD

where a, b, c, and d represent the coefficient of reactants A, B, C, and D respectively, what is the rate at which the reaction will proceed?

Answer 1

For the generic chemical reaction

aA + bB ⇒ cC + dD

the rate expression is:

rate = k_obs [A]^x [B]^y

where k_obs is the rate constant, and x and y are the reaction orders of A and B, respectively.

Question 2

How is the overall order of a chemical reaction calculated?

Answer 2

The overall order of a chemical reaction is the sum of the reaction orders of all the reactants.

For the rate expression: rate = k_obs [A]^x [B]^y
the overall order is the sum x+y. k_obs is the rate constant, and x and y are the reaction orders of A and B respectively.

Question 3

Define:

the rate constant of a chemical reaction

Answer 3

A chemical reaction’s rate constant, k_obs, is the rate at which the reaction proceeds when the concentration of all reactants is 1M or 1 atm.

Question 4

Define:

a zeroth order reaction

Answer 4

A zeroth order reaction is one whose overall reaction order is zero, and is independent of reactant concentration.

A zeroth order reaction’s rate is constant, and can be given by: Rate = k_obs

Question 5

If a chemical reaction is zeroth order in [A], with A being one of the reactants, how does the reaction rate vary if [A] doubles?

Answer 5

The reaction rate is unchanged, since there is no correlation between the value of [A] and rate in a zeroth order reaction.

If the reaction is zeroth order in [A], that means that the rate can be described as: rate = k_obs [A]⁰ = k_obs

Question 6

Define:

a first order reaction

Answer 6

A first order reaction is one whose overall reaction order is 1, and whose rate depends on the concentration of only one reactant, in a linear fashion.

If A is the reactant on which the reaction rate depends, the rate will be:
Rate = k_obs [A]¹

Question 7

If a chemical reaction is first order in [A], how does the reaction rate vary if [A] decreases by a particular amount?

Answer 7

The reaction rate decreases by the same amount that the concentration did.

First order in [A] means the rate law is: rate = k_obs [A]¹
Let [A]_orig = x.
Then rate_orig = k_obs * x.
If [A] decreases, then rate_new = k_obs (decreased x) = (decreased) * rate_orig

Question 8

If a chemical reaction is first order in [A], how does the reaction rate vary if [A] doubles?

Answer 8

The reaction rate doubles.

First order in [A] means the rate law is: rate = k_obs [A]¹
Let [A]_orig = x.
Then rate_orig = k_obs * x.
If [A] doubles, then rate_new = k_obs (2x) = 2 * rate_orig

Question 9

Define:

a second order reaction

Answer 9

A second order reaction is one whose overall reaction order is 2, and whose rate either depends on one reactant to the second order, or two separate reactants to the first order.

If the reactants for the reaction are A and B, the rate will be one of:
rate = k_obs [A]²
or rate = k_obs [B]²
or rate = k_obs [A]¹[B]¹

Question 10

If a chemical reaction is second order in [A], how does the reaction rate vary if [A] increases by a specific amount?

Answer 10

The reaction rate increases proportionally by the square of that specific amount.

Second order in [A] means the rate law is: rate = k_obs [A]²
Let [A]_orig = x
Then rate_orig = k_obs * x².
If [A] increases, then rate_new = k_obs (increased x)² = (increase)² * rate_orig

Question 11

If a chemical reaction is second order in [A], how does the reaction rate vary if [A] triples?

Answer 11

The reaction rate increases by a factor of 9.

Second order in [A] means the rate law is: rate = k_obs [A]²
Let [A]_orig = x
Then rate_orig = k_obs * x².
If [A] triples, then rate_new = k_obs (3x)² = 9 * rate_orig

Question 12

If a chemical reaction is first order in both [A] and [B], how does the reaction rate vary if [A] triples, while [B] is reduced by half?

Answer 12

The reaction rate increases by a factor of 1.5.

If the reaction is first order in [A] and [B] means the rate law is: rate = k_obs [A]¹ [B]¹

Let [A]_orig = x and [B]_orig = y
Then rate_orig = k_obs * x * y.
If [A] triples and [B] decreases by half, then rate_new = k_obs * (3x) * (½y) = 1.5 rate_orig

Question 13

For a reaction with chemical A as reactant, and kinetic data given below, what is the reaction’s overall rate law?

Answer 13

Rate = 5 [A]²

To determine the reaction order for A, see how varying [A] affects the rate. Between Trials 1 and 2, [A] increases by a factor of 2, and the rate increases by a factor of 4.

Since the rate increases by a factor of the concentration increase to the second power, the reaction must be second order in [A].

Once the reaction orders are solved, plug in the value of [A] for either trial to solve for k_obs.

Question 14

For a reaction with chemicals A and B as reactants, and kinetic data given below, what is the reaction’s overall rate law?

Answer 14

Rate = 2 [A]¹ [B]⁰

Between Trials 1 and 2, [A] doubles, while [B] stays constant, and the reaction rate doubles, so the reaction order for A is 1.

Between Trials 2 and 3, [B] doubles, while [A] stays constant, and the reaction rate is unchanged, so the reaction order for B is 0.

Plugging in the values [A] = 1 and [B] = 1 from Trial 1 delivers a final value of 2 for k_obs.

Question 15

For a reaction with chemicals A and B as reactants, and kinetic data given below, what is the reaction’s overall rate law?

Answer 15

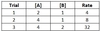
Rate = 2 [A]¹ [B]²

Between Trials 1 and 2, [A] doubles, while [B] stays constant, and the reaction rate doubles, so the reaction order for A is 1.

Between Trials 2 and 3, [B] doubles, while [A] stays constant, and the reaction rate increases by a factor of 4, so the reaction order for B is 2.

Plugging in the values [A] = 2 and [B] = 1 from Trial 1 delivers a final value of 2 for k_obs.

Question 16

What is a reaction’s rate-determining step?

Answer 16

A chemical reaction’s rate-determining step is the slowest sub-step of a reaction. As such, it limits how fast the overall reaction can proceed.

Ex: the reaction
NO₂ + CO ⇒ NO + CO₂
is actually two sub-reactions,
NO₂ + NO₂ ⇒ NO₃ + NO (slow)
NO₃ + CO ⇒ NO₂ + CO₂ (fast)
The slow first step is the rate-determining step, and limits the overall reaction rate.

Question 17

How is a reaction’s rate-determining step identified?

Answer 17

The rate-determining step can be identified because the substances which appear in the rate law must be reactants in the rate-determining step.

Ex: If the overall reaction rate depends only on [NO₂] for the following steps:
NO₂ + NO₂ ⇒ NO₃ + NO
NO₃ + CO ⇒ NO₂ + CO₂
Then the first step, in which NO₂ appears as a reactant, must be the rate-determining step.

Question 18

Define:

an intermediate in a chemical reaction

Answer 18

A reaction intermediate is a species that plays a role in a reaction, but does not appear in the overall chemical equation.

An intermediate can be identified by the fact that it is a product of an early reaction step, and a reactant in a later one.

Question 19

Identify the intermediate in the reaction below:

Overall Reaction: 2 O₃ ⇒ 3 O₂
Step 1: O₃⇒O₂+ O
Step 2: O + O₃⇒ 2 O₂

Answer 19

O is the intermediate.

O is a product of Step 1, and a reactant of Step 2, and does not appear in the overall reaction. Therefore, it is an intermediate.

Question 20

What is the molecularity of an elemental chemical reaction?

Answer 20

Molecularity is the number of reactant molecules taking part in a single reaction step. Therefore, it is a concept that can only be applied to elementary reactions.

A reaction involving one molecule of reactant is unimolecular; two is bimolecular; and three is termolecular.

Question 21

What is the molecularity of the elementary reaction below?

NO + NO₃→ 2NO₂

Answer 21

NO + NO₃→ 2NO₂

The reaction has two individual molecules as reactants. Therefore, it is bimolecular.

Question 22

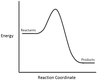
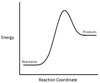
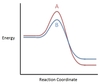
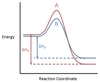
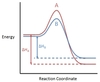
In the chemical reaction energy profile shown below, where are the reactants and the products located?

Answer 22

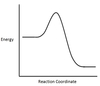
In energy profiles, the reactants are on the left, at the beginning of the reaction.

The products are on the right, at the end of the reaction.

Question 23

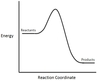
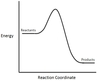
In the chemical reaction energy profile below, what is the quantity A?

Answer 23

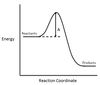
A is the activation energy E_a.

The activation energy determines how much energy the reactants require to convert to the activated complex, or transition state. The higher the activation energy, the slower the reaction proceeds.

Question 24

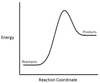
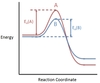
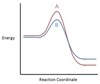
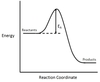
In the chemical reaction energy profile below, what portion of the reaction is located at point C?

Answer 24

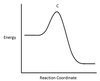
The reaction’s transition state is located at the peak of the reaction profile.

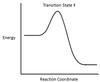
The transition state, also known as the activated complex, is the chemical intermediate between the reactants and the products. Since it is the highest energy point in the reaction profile, it is the least stable part of the reaction, and the reaction rapidly proceeds to the products once the transition state is reached.

Question 25

In the chemical reaction energy profile below, what is the quantity B?

Answer 25

B is the reaction enthalpy, ΔH.

The reaction enthalpy is a measure of the difference in energy level between the reactants and the products.

If ΔH < 0, the reaction is exothermic.
If ΔH > 0, the reaction is endothermic.

Question 26

Is the chemical reaction being depicted below endothermic or exothermic?

Answer 26

It is exothermic.

The products’ enthalpy is lower than the reactants’, so ΔH < 0, meaning the reaction is exothermic.

Question 27

Is the chemical reaction being depicted below endothermic or exothermic?

Answer 27

It is endothermic.

The products’ enthalpy is higher than the reactants’, so ΔH > 0, meaning the reaction is endothermic.

Question 28

What is the Arrhenius equation?

Answer 28

The Arrhenius equation relates a reaction’s activation energy E_a, rate constant k_obs, the temperature of the chemical system T, and the ideal gas constant R.

Question 29

According to the Arrhenius equation, how does a reaction’s rate vary as temperature is increased?

Answer 29

As the temperature increases, the reaction’s rate increases as well.

As T increases, the term e^-E_a/RT, which starts out as a small fraction, moves closer and closer to 1, raising the calculated value of k_obs and speeding up the reaction.

In general, the Arrhenius equation predicts that a reaction’s rate will double for every 10ºK increase in temperature.

Question 30

Of the two reactions shown below, which is kinetically preferred?

Answer 30

Reaction B is kinetically preferred.

A reaction’s activation energy determines whether it is kinetically preferred or not. In this case, E_a is smaller for reaction B than it is for reaction A. So reaction B runs faster, and is kinetically preferred.

Question 31

If reactions A and B are run simultaneously at low temperature, which set of products will result?

Answer 31

At low temperature, reaction B’s products will dominate.

At low temperatures, the kinetically preferred reaction will be favored. Since B is kinetically preferred, it will dominate under these conditions.

Question 32

Of the two reactions shown below, which is thermodynamically preferred?

Answer 32

Reaction A is thermodynamically preferred.

A reaction’s enthalpy change determines whether it is thermodynamically preferred or not. In this case, ΔH_A is larger in magnitude than ΔH_B, so the products of A are more thermodynamically stable, and reaction A is thermodynamically preferred.

Question 33

If reactions A and B are run simultaneously at high temperature, which set of products will result?

Answer 33

At high temperature, reaction A’s products will dominate.

At high temperatures, the thermodynamically preferred reaction will be favored. Since A is thermodynamically preferred, it will dominate under these conditions.

Question 34

Define:

a chemical catalyst

Answer 34

A catalyst is a chemical which participates in a reaction and serves to increase the reaction’s rate, usually by lowering the activation energy for the reaction. Catalysts are not themselves depleted by the reaction.

Question 35

How does a chemical catalyst change the energy profile of a chemical reaction?

Answer 35

Chemical catalysts decrease a reaction’s activation energy.

Ex: The below energy profile demonstrates positive catalysis. Note that E_a decreases, but ΔH is unaffected by the catalyst.

Question 36

What role do enzymes play in chemical reactions?

Answer 36

Enzymes serve as catalysts in chemical reactions.

Therefore, they speed up or slow down reactions, but they are not affected by the reaction, and they cannot change the thermodynamic favorability of a reaction.

Question 37

What is the difference between a homogeneous catalyst and heterogeneous catalyst?

Answer 37

• A homogeneous catalyst is in the same phase as the remaining reactants.
• A heterogeneous catalyst is in a different phase from the remaining reactants.

Question 38

Define:

autocatalysis

Answer 38

A reaction undergoes autocatalysis if the product of the reaction further catalyzes the reaction.