Key Math Notes

Question 1

Dilution or Mixture

Answer 1

Where w=weaker solution,

s=stronger solution,

and d=desired solution

______________

(w%-d%)w = (s%-d%)s

Question 2

GROUP

Answer 2

Group 1

+ Group 2

+ Neither

• Both

Total #

Question 3

Permutation

of ways to arrange elements sequentially (with repitition)

Answer 3

_nP_k=

__n!_\_

(n - k)!

n= # in the large group

k= # being arranged

Question 4

COMBINATION

When the order in an arrangement of the smaller group being drawn from the larger group doesn’t matter

Answer 4

_nC_k =

_\_n!__

k! (n - k)!

n = # in larger group

k = # being chosen

Question 5

COMBINED WORK

Answer 5

The inverse of the time it would take everyone working together equals the sum of the inverse of the times it would take each owrking individually

1/r + 1/s = 1/t

r and s = the time it would take individuals working seperately

t = the time it would take them working together

Question 6

P E M D A S

Answer 6

Parantheses

Exponents (or radicals)

Multiplication & Division

(from left to right)

Addition & Subtraction

(from left to right)

Question 7

Multiples of 3

Answer 7

sum of digits is multiple of 3

Question 8

Multiples of 4

Answer 8

last two digits are a multiple of 4

Question 9

Multiples of 6

Answer 9

Even number whose sume is multiple of 3

Question 10

Multiples of 9

Answer 10

sum of digits is multiple of 9

Question 11

Multiples of 12

Answer 11

a multiple of both 3 and 4

Question 12

Max and Minimum Sides of a triangle

Answer 12

The third side of a triangle is between the positive difference and sum of the other two sides.

Question 13

Regular Polygon Angles

Answer 13

n = # of sides

Sum of interior angles:

(n - 2) x 180

Degree of one angle:

(n - 2) x 180

n

Question 14

LENGTH of an ARC

Answer 14

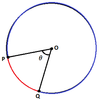
ARC =

θ = angle

(θ / 360) x 2πr

Question 15

AREA of a SECTOR

Answer 15

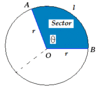
SECTOR =

θ = angle

(θ / 360) x πr²

Question 16

ARC

SECTOR

SEGMENT

Answer 16

Question 17

(x^a)(x^b)

Answer 17

x^a+b

Question 18

x^a / x^b

Answer 18

x^a-b

Question 19

(x^a)^b

Answer 19

x^ab

Question 20

0^x

Answer 20

0

Question 21

x⁰

Answer 21

1

Question 22

0⁰

Answer 22

Undefined

Question 23

x^-2

Answer 23

1 / x²

Question 24

x^1/3

Answer 24

3√x

Question 25

x^1/2

Answer 25

√x

Question 26

√x + √x

Answer 26

2√x

Question 27

(a√b)(c√d)

Answer 27

(ab)(√b+d)

Question 28

Answer 28

isosceles triangle

2 angles are the same

2 sides are the same

Question 29

Answer 29

Equalateral Triangle

All sides are equal

All angles are 60^o

Question 30

Answer 30

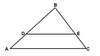
Similar Triangles

Corresponding angles are equal

Sides are proportional

Question 31

Pythagorean Theorem

Answer 31

With right triangles only:

a² + b² = c²

Question 32

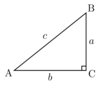
Special Right Angles

Side proportions (4)

Answer 32

3 : 4 : 5

5 : 12 : 13

30^o - 60^o - 90^o

= 1 : √3 : 2

45^o - 45^o - 95^o

= 1 : 1 : √2

Question 33

SLOPE

Answer 33

RISE / RUN

Change in Y / Change in X

Question 34

SIMPLE

INTEREST

Answer 34

Interest Earned (I) =

Principle (P)

x interest rate (r)

x time, in years (t)

I = Prt

Question 35

COMPOUND

INTEREST

Answer 35

Interest Earned (I) =

Principle (P)

Interest Rate (r)

time, in years (t)

of times compounded annually (c)

I = P ( 1 + r/c)^tc

Question 36

Counting consecutive numbers

Answer 36

A => B =

B - A + 1

Question 37

Sum of Consecutive numbers

Answer 37

Sum = Average x # of terms

A => B

(A + B) / 2 = Average of terms

B - A + 1 = # of terms

(A + B) / 2

Question 38

Recognize this Polynomial

ab + ac

Answer 38

a (b + c)

Question 39

Recognize this Polynomial

a² + 2ab + b²

Answer 39

(a + b)²

Question 40

Recognize this Polynomial

a² - 2ab + b²

Answer 40

(a - b)²

Question 41

Recognize this Polynomial

a² - b²

Answer 41

(a + b)(a - b)

Question 42

WEIGHTED

AVERAGE

Answer 42

Group A Average = x

Group B Average = y

Group A is z times as big as Group B

(zx + (1)y) / (z+1)

Question 43

COMMON FACTORS

eg: 135 and 225

Answer 43

1^st: find the prime factors in each #

135 = 3 x 3 x 3 x 5

225 = 3 x 3 x 5 x 5

2^nd: find the prime factors they have in common

3 x 3 x 5

3^rd: multiply these common factors in every combination

3 x 3, 3 x 5, 3 x 3 x 5

So, common factors are 3, 5, 9, 15, 45

Question 44

STANDARD

DEVIATION

Answer 44

1. Find the mean of the set
2. Find the difference between the mean and each value
3. Square each of the differences
4. Find the average of the squared differences (3)
5. Take the positive square root of the average (4)