IV) Time & Uncertainty Flashcards
What does a consumer face when there is 2 periods of time, 2 incomes (x), and he cannot borrow nor lend?
He faces a trade off consumption between period 1 to period 2.
What is the budget constraint if the consumer chooses to lend money at c1?
c2= x2+(x1 - c1)(1+r)
What is the budget constraint if the consumer decides to borrow money?
c2= x2- (c1-x1)(1+r)
What will be the future value budget constraint?
(1+r)c1+c2 = (1+r)x1+x2
What is the present value budget constraint?
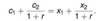
Draw the intertemporal budget constraint:
What is the effect of a change in the r?
Generally, is r different or the same for borrowing and lending?
It is different.
What do you compute to choose what is the best investment between 2?
How do you compute it?
Net Present Value for the 2 investments.
NPV = r1+r2/(1+r) +…. + rT/(1+r)T-1
According to the NPV, when is investment the best?
The higher the NVP, the better the investment.
The revenue can be lower at some periods, but on average, it is greater.
What is a bond?
It is characterized by 3 parameters:
- A coupon (amount paid every period): x
- A maturity date T
- A face value (paid at the end of the maturity): F
What si the NPV of a bond?
NPV = x/(1+r) + x/(1+r)2 +… + F/(1+r)T
What is a lottery?
How is it represented?
List of prizes together with the probabilities of obtaining the prizes.
L = (0, 1000), (0,98, 0,02)
How do you compute the E of a lottery?
L = (0, 1000), (0,98, 0,02)
E(L) = 0*0,98 + 1000*0,02
What can we compare choices under uncertainty to?
Lotteries.
Consumer doesn’t have preferences over bundles anymore but over lotteries.
What does describe a contingent consumption plan?
In each possible contingency, it describes the consumption of the agent.
What is an insurance?
How is it composed?
Way to modify contingent consumption plans in order to smooth consumption.
It is composed of:
- a premium which is paid by the consumer, no matter the state.
- a payment paid by the insurance during the bad state.
When are 2 lotteries independent?
If and only if L2≻L3 and L’2≻L’3
What is the expected utility?
Decomposition of the choice into:
- A probability distribution over outcomes
- A utility function u(c) over outcomes.
=> Utility is linear in probabilities and risk attitude is captured by the utility function.
L = (c1, c2), (p1, p2)
U(L) = p1u(c1) + p2u(c2)
In the expected utility th, of what type are utilities?
They are cardinal.
What are the classical utility functions?
- Linear quadratic: u(c) = ac - bc2
- Exponential
- u(c) = cˠ
- u(c) = eρx
- Log: u(c) = ln c
How do we determine risk aversion?
- Risk aversion: EU(L) < u(EL)
The utility function of participating the lotery is concave. second derivative negative
- Risk neutral: EU(L) = u(EL)
Utility function of participating is a line.
- Risk loving: EU(L) > u(EL)
Utility function of participating is convex. 2nd derivative positive.
What is the certainty equivalent?
c(L) which solves the equation:
U(c(L)) = EU(L)
For risk averse person, c(L) < EL. c(L) is always lower than the expected value of the lottery.
How do you know that an agent is more risk averse than another?
- Risk premium is higher (u(EL)-Eu(L))
- Certainty equivalent is lower
- Concave function
- compute the Arrow Pratt indicator to measure the absolute / relative risk aversion:
How do you measure the risk of 2 lotteries?
When a risk averse agent chooses ont lottery compared to another, it is less risky.
So it depends…
What is a fair insurance?
The company doesn’t make positive expected profit.
ɣK = (1-p)K
How do you determine the best portfolio choice?
r is the return of a bond and σ the σ of the stocks.
MRS increases in x (the fraction of the portfolio invested in the risky asset.
Summary 1:
Summary 2:
