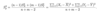Interval Estimation

Question 1

Define a confidence interval

Answer 1

Question 2

Give the equation for S²

Answer 2

Note: We assume the sample comes from a normal distribution. S2 is a random variable as it is a transformation of the random sample variables

Question 3

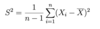
Give the equation for x̄ (X bar)

Answer 3

Note: we assume the sample comes from a normal distribution. X bar is a random variable as it is a transformation of the random sample variables

Question 4

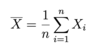
Give the test statistic needed to construct a (1-α) confidence interval for unknown mean µ and we know population variance σ²

Answer 4

This can be rearranged to find µ

Question 5

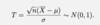
Give the test statistic needed to construct a (1-α) confidence interval for unknown mean µ and we do not know population variance

Answer 5

Note: we can rearrange T to find µ

Question 6

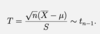
Describe the width of an approximate confidence interval for the population mean

Answer 6

Note: if σ is unknown it can be replaced by S (the sample standard deviation)

Question 7

Describe how to find the confidence interval for a population mean if the distribution is not necessarily normal and we know the variance.

Answer 7

• Using central limit theorem, all IIDs of any distribution are approximately normal. Generally, n≥30 is sufficient to make this assumption.
• Variance is often a function of E(X) (Ie one parameter distributions) and so T can be modified for different distributions. See below

Question 8

Describe how to find the confidence interval for a population mean if the distribution is not necessarily normal and we do not know the variance.

Answer 8

Note that this approximation is valid whenever CLT is valid.

As we make no assumptions we must be sure that the sample is very large for the CI to be valid.

Question 9

Give the test statistic needed to construct a (1-α) confidence interval for unknown variance σ² and we know the population mean µ.

Answer 9

This can be rearranged for σ²

Question 10

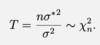
Give the test statistic needed to construct a (1-α) confidence interval for unknown variance σ2 and we don’t know the population mean µ.

Answer 10

This can be rearranged for σ²

Question 11

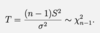
Give the test statistic needed to construct a (1-α) confidence interval for the difference in means between two independent normal distributions and where we know the variance

Answer 11

Question 12

Give the test statistic needed to construct a (1-α) confidence interval for the difference in means between two independent normal distributions and where we don’t know the variance

Answer 12

We assume the variances of the two distributions are equal.

Question 13

Give the test statistic needed to construct a (1-α) confidence interval for the difference in means where we have one sample of pairs

Answer 13

Question 14

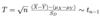
Describe the random sample of differences

Answer 14

Question 15

Give the test statistic needed to work out the confidence interval for the ratio of variances from two normal populations when the samples are independent and we know the means

Answer 15

Question 16

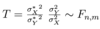
Give the test statistic needed to work out the confidence interval for the ratio of variances from two normal populations when the samples are independent and we don’t know the means

Answer 16

Question 17

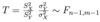
Define a simple hypothesis

Answer 17

A hypothesis is called simple if it completely determines the distribution of the observed data; an example of a simple hypothesis is θ = θ₀ if θ is the only parameter in the model.

Question 18

Define a composite hypothesis

Answer 18

The hypothesis is called composite if it contains an unknown parameter. an example is a hypothesis of the form θ > θ₀, since it does not exactly determine all the parameters.

Question 19

Define a type 1 error

Answer 19

H₀ is rejected even though it is true

Question 20

Define a type 2 error

Answer 20

H₀ is not rejected even though it is false

Question 21

Define the level of significance for a hypothesis test

Answer 21

Question 22

Define the power of a test

Answer 22

Question 23

Give the equation for S_p²

Answer 23