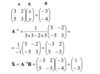Interests Flashcards
Simple interest =
Any money saved that receives an interest payment at the end of each period which is NOT REINVESTED
SI = P × (i/100) × t
SI = Simple Interest
P= Principal (initial amount)
i = rate of interest (as a percentage)
t = number of time periods
Compound interest =
Any money saved then receives an interest payment which is then REINVESTED.
(Most types of account receive (or pay) compound interest (CI).)
At = P× (1+ i)t
At = Amount after t time periods P = Principal or sum invested i = compound interest rate (as a decimal)
t = end of time period in question
Compounding factor =
(1+i)t
Formula for total compound interest paid
We merely take the end value after period t (At) and substract the initial amount P to find the total compound interest paid over this time period.
CIt = At - P
CIt = P(1 + i)t - P
Detailed table of At = P(1 + i)t for P=100, t=5(years) and i=0,1
(example in slide)
P=100
i=0,1
Interest Rate has to be expressed as …
A rate per unit interval of time.
It is not restricted to one year: could be a half-year, a quarter of a year, an hour or any other time interval
Effective Rate of Interest =
The actual rate of accumulation over the stated time interval. (when compounding)

Nominal Rate of Interest =
The nominal rate is the stated interest rate for a unit interval of time, which may be different from that used for accumulating interest, e.g.:
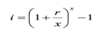
– 3% per half-year would be quoted as being “6% per annum, payable half-yearly”.
Let r be the nominal rate of interest per annum that is payable x times a year.
• The equivalent or effective rate of interest per annum ( i ) is given by:
The accumulated amount of an investment (P) at a nominal rate of interest per annum, payable x times a year (r) for t years is therefore given by:
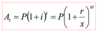
Continuous Compounding Formula :
Pert
Compounding formula:
At=P×(1+i)t
Discounting Formula=
(Present Value)
(i.e. PV of redemption value for bonds)
The discounting process essentially involves reversing the growth process involving compound interest rates.
i.e. What is the present value of £133.10 received after 3 years at a 10 percent interest rate ?
PV = At(1+ i)−t
Present value=
Referred to as discounting
What value, P, must be invested now in order to obtain a particular future sum, At (i.e. the value of tomorrow’s money today)
Payback Period (PBP) =
The payback period is the time needed for the nominal cash generated by a project (sum of the yearly cash flows) to be equal to the cash injection needed.
In other words, payback occurs during the year in which positive cumulative cash flows is first achieved.
Average Rate of Return (ARR) =
ARR is the average percentage return per time period (normally one year) on the initial capital outlay over the expected life of the project:

Net Present Value (NPV) =
The total of the PVs of the cash inflows (revenues) less the initial capital outlay is the Net Present Value (NPV)
NPV > 0 ⇒ Value created
• Project with largest NPV according to the assumed rate of interest is the most profitable:
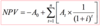
A project has the following cash flow (£)
Now -1200 Yr1=700 Yr2=800
What is the NPV if the discount rate is:
(a) 5%

.The higher the rate of discount we use in calculating the NPV…
The lower the value of NPV, i.e. there is an inverse relationship
If projects have different degrees of ‘risk’, then a higher rate of discount should often be applied to the riskier project(s)
Internal Rate of Return (IRR) =
The discount rate (i) which makes the net present value of a project equal to zero (i.e. it is the effective interest rate you are earning on the money you invest in the project)

Formule équation second degré (quadratic)=
Δ=b2-4ac
Si Δ=0, x= -b/(2a)
Si Δ>0, 2 solutions:
(-b± √Δ)/2a
Linear Interpolation Method (to be used to calculate IRR if project has more than 2 periods)
Calculate the NPV with two different discount rates, such that one (R1) gives a positive and the other (R2) a negative NPV
- Calculate IRR by using the formula:

Depreciation =
Just as some investments grow at a simple or compound rate due to interest rates on an initial amount, other investments might decline as a result of depreciation:
book value of capital equipment and other assets reduce through simple ‘wear and tear’
Straight line depreciation=
Reduces the value of capital by the same absolute amount each year
Annual depreciation =
(initial value - scrap value)/estimated life

Reducing Balance Depreciation: =
Most capital items do not depreciate in a linear fashion:

Sum (Sn) of a finite geometric progression:
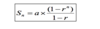
Sinking Fund =
Regular savings arrangement with a financial institution.
An amount P is saved regularly for a specified period at a fixed rate.
The accumulated capital over the period is then computed as just described
Present Value Annuities Formula =
(i.e: mortgages, annuities, coupons from bonds)

Future Value Annuities formula =

Repayment Mortgage
- When a mortgage is taken out on a property it can be repaid by a series of regular payments.
- The mortgage is thus the present value of all future instalments
Interest Only Mortgage
- Only the interest is paid over the mortgage period.
- The capital (loan) is paid in a lump sum at the end of the mortgage period and is normally accumulated by a regular savings arrangement.
- The monthly cost of the mortgage is thus the monthly interest plus the amount to be accumulated (in a sinking fund):
Monthly Cost = Interest + Savings Amount
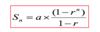
Annual Percentage Rate
(i.e. 1 year loan at 2% per month)
APR = [1(1 + i)t - 1] * 100
The equation of a straight line is
y = ax + b
Where:
b is the intercept
a is the slope or gradient
Where we have the maximum at x1 =
the value of the first derivative is zero, and the value of the second derivative (at x1) is negative.
Where we have the minimum at x2 =
The value of the first derivative is zero, and the value of the second derivative (at x2) is positive
Total revenue (TR)=
Price (P) × Quantity (Q)
Average revenue (AR) =
TR/Q = (P*Q)/Q = P
AR=Price (P)
Total Cost (TC) =
equals total fixed cost (TFC) plus total variable cost (TVC)
TC = TFC + TVC
Average total Cost (ATC) =
ATC = TC/Q
Total profit (TP) =
TP = TR - TC
To find the Marginal Revenue (MR) :
Differentiate (Dériver) Total Revenue (TR) with respect to q (utiliser q (quantité) à la place x)
To find the Marginal Cost (MC) :
Differentiate (dériver) Total Cost (TC) with respect to q
Profit is maximized when:
Marginal Cost = Marginal Revenue
Differentiate =
Dériver
Gradient of a line =
= slope = rise/run = y/x
f’=
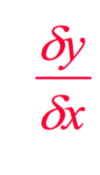
f’’ =
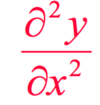
La dérivée de est ?

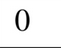
La dérivée de

La dérivée de u + v est
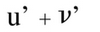
La dérivée de
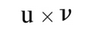
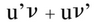
La dérivée de
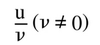
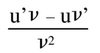
La dérivée de
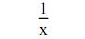
Pour x ≠ 0

La dérivée de √x
Pour x > 0
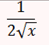
La dérivée d’une constante k est:
0
La dérivée de x est :
1
La dérivée de x2 est :
2x
La dérivée de x3 est :
3x2
La dérivée de xn est :
(si n est un entier)
n*xn-1
La dérivée de ln(x) est =
x’/x
La dérivée de ex =
x’ * ex
What is the price elasticity of demand ?
E = - Percentage change in demand / Percentage in change in price
dQ/dP = dérivée

Elastic Demand =
The percentage change in demand is greater than the percentage change in price.
E is greater than 1.
Inelastic Demand
The percentage change in demand is less than the percentage change in price. E is less than 1.
What is EOQ ?
Economic Order Quantity (EOQ)
– Ordering quantity that minimizes total inventory cost.
– Total inventory cost is the sum of carrying and ordering cost
How to find EOQ ?
- Differentiate Total Cost w.r.t. Q and equate to 0 (when costs are at minimum)
Q = (2CoD/Cc)1/2
Where:
• Q is the Economic Order Quantity
• Co is the ordering cost for one order
• D is the demand per time period
• Cc is the carrying cost per item per time period
What is integration ?
The reverse operation of differentiation
=> the rules of integration reverse differentiation.

Integrate of y = axn is:
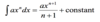
Integrate of y = a is:
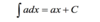
Integrate of y = eax :

Integrate of
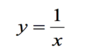
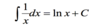
La taille d’une matrice de lit toujours ..
Lignes x colonnes
Si on multiplie une matrice 3x4 et 4x1, qu’elle sera sa taille ?
3x1
A vector matrix has…
One of its dimensions equal to 1 (it is either a row or a column matrix)
- (3 -2 7)
- ( 4 )
( 9 )
A square matrix has…
The same number of rows and columns.
A diagonal matrix is …
A square matrix with all elements zero, but those in the main diagonal (top left to right bottom).
( 1 0 0 0 )
( 0 1 0 0 )
( 0 0 1 0 )
( 0 0 0 1 )
The Identity Matrix =
Is a diagonal matrix, whose non-zero elements are equal to 1. Often called I
( 1 0 0 )
I = ( 0 1 0 )
( 0 0 1 )
Adding and Subtracting Matrices :
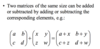
Multiplying a Matrix by a Constant :
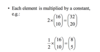
Multiplying Two Matrices :
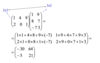
If we have two matrices A and B, we have:
A+B = B+A
but we are unlikely to have A×B = B×A
The inverse matrix
The inverse matrix has the property that:
AA−1 =A−1A=I
Find the inverse matrix :
Note:A matrix that does not have an inverse is called singular and its determinant is equal to zero.
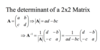
Applying matrices to solve simultaneous equations:
(i.e. :
3x + 2 y = −3
5x + 3y = −4 )
- AX = B
- X = A-1 B