Important trig Flashcards
(12 cards)
1 + tan2x = ?
1 + tan2x = sec2x
cos2x + sin2x = ?
cos2x + sin2x = 1
sin2x = ?
sin2x = 2sinxcosx
cos2x = ?
cos2x = cos2x - sin2x
= 2cos2x - 1
= 1 - 2sin2x
1/cos =
1/sin =
1/tan =
1/cos = sec
1/sin = cosec
1/tan = cot
sinhx =
coshx =
tanhx =
sinhx = (ex - e-x) / 2
coshx = (ex + e-x) / 2
tanhx = (ex - e-x) / (ex + e-x)
Derivative of sinh = ?
Derivative of cosh = ?
Derivative of tanh = ?
Derivative of
sinh <=> cosh
Derivative of tanh = sech2
What are the steps to differntiating inverse trig functions?
- Eliminate the inverse
- Differentiate wrt x (usually means add a dy/dx)
- Rearrange for dy/dx
- Get the RHS in terms of x.
Name the missing lengths and angles.

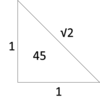
Name the missing lengths and angles.
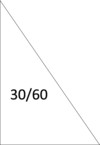

What is the domain of:
arcsin?
arcos?
The domain of arcsin is the domain where sin is one-one, therefore -π/2 to π/2.
The domain of arcsin is the domain where sin is one-one, therefore 0 to π.

What is dy/dx of an inverse function f-1(x)?
dy/dx = 1/ f (f-1(x))
Remember if f(x) = 0 then f-1(0) = x


