Imaginary and Complex Numbers

Question 1

If z = a + bj, what is the complex conjugate of z?

Answer 1

If z = a + jb

then the complex conjugate is:

ź (or z*) = a - jb

Question 2

What is j¹?

Answer 2

j¹ = j

or

j = ‚/-1

Question 3

What does j² evaluate to?

Answer 3

j² = -1

Question 4

What does j³ evaluate to?

Answer 4

j³ = -j

Question 5

What does j⁴ evaluate to?

Answer 5

j⁴ = j²•j²

= -1 • -1

= 1

Question 6

What does √-1 x √-1 evaluate to?

Answer 6

√-1 x √-1 = j x j

= j²

= -1

Question 7

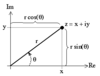
What is the argument of a complex number?

give the formula

Answer 7

The argument of a complex number is the angle between the Re axis and the position vector of the complex number as depicted on an Argand diagram, such that -π < arg z ≤ π. This holds true as long as z ≠ 0.

Arg (z) = tan^-1 Im(z) / Re(z), z ≠ 0

also

Arg (z) = sin^-1 Im(z) / |z|, z ≠ 0

also

Arg (z) = cos^-1 Re(z) / |z|, z ≠ 0

Question 8

What is the modulus of an imaginary number?

Give formula

Answer 8

The Modulus of an imaginary number is the scalar length (magnitude) of the position vector of the imaginary number as depicted on an Argand diagram.

|z| = r = Sqrt (Re[z]² + Im[z]²)

Question 9

Write the complex number z = x + jy in polar form.

Answer 9

Given that |z| = r = Sqrt (Re[z]² + Im[z]²)

and therefore Re(z) = r cosø

and also Im(z) = r sinø

z = r cosø + j r sinø

= r (cosø + j sinø)

Question 10

Convert the Complex number z = r (cosø + j sinø) to Exponential form.

Answer 10

Given that (cosø + j sinø) = e^jø

z = r (cosø + j sinø)

becomes

z = r(e^jø)

=re^jø

if and only if ø is in radians

Question 11

Simplify j⁴²

Answer 11

j⁴² = ( j⁴)¹⁰ ( j²)

= (1)¹⁰ (-1)

= -1

Question 12

Simplify j¹²

Answer 12

j¹² = ( j⁴)³

= (1)³

= 1

Question 13

Simplify j¹¹

Answer 13

j¹¹ = ( j⁴)² ( j³)

= (1)² ( - j)

= - j

Question 14

Simplify j ^{- 8}

Answer 14

j ^{- 8} = ( j ^{- 4})²

= (1)²

= 1

Question 15

Simplify j^-1

Answer 15

Start with j² = -1

divide both sides by j

j = -1/j

= - j^-1

multiply both sides by -1

j^-1 = - j

Question 16

Simplify j^-2

Answer 16

j^-2 = (j²)^-1

= (-1)^-1

= -1

Question 17

Simplify j ^-3

Answer 17

j ^-3 = (j ^-2) j ^-1

= (-1) (-j)

= j

Question 18

SImplify j ^-4

Answer 18

j ^-4 = (j ^-2)²

= (-1)²

= 1

Question 19

Simplify j ^{- 19}

Answer 19

j ^{- 19} = ( j^-4)⁴ ( j ^{- 3})

= (1)⁴ ( j)

= j

Question 20

Simplify j ^{- 30}

Answer 20

j ^{- 30} = ( j ^{- 4})⁷ ( j ^{- 2})

= (1) (-1)

= -1

Question 21

Simplify j ^{- 15}

Answer 21

j ^{- 15} = ( j ^{- 4})³ ( j ^{- 3})

= (1)³ ( j)

= j

Question 22

Simplify j ^{- 32}

Answer 22

j ^{- 32} = ( j ^{- 4})⁸

= (1)⁸

= 1

Question 23

Simplify j ^{- 13}

Answer 23

j ^{- 13} = ( j ^{- 4})³ ( j ^-1)

= (1)³ (- j)

= - j

Question 24

Simplify j ^{- 23}

Answer 24

j ^{- 23} = ( j ^{- 4})⁵ ( j ^{- 3})

= (1)⁵ ( j)

= j

Question 25

In the complex number z = 3 + j5 what is the real part and what is the imaginary part? Use proper notation.

Answer 25

The parts of the complex number z = 3 + j5 are as follows:

Re(z) = 3 (the real part)

Im(z) = 5 (the imaginary part)

So, a complex number z = Re(z) + j Im(z)

Question 26

Complete the following complex number addition:

(4 + j5) + (3 - j2)

Answer 26

(4 + j5) + (3 - j2) = 4 + j5 + 3 - j2

= (4 + 3) + j(5 - 2)

= 7 + j3

Question 27

Complete the following complex number subtraction:

(4 + j7) - (2 - j5)

Answer 27

(4 + j7) - (2 - j5) = 4 + j7 - 2 + j5

= (4 - 2) + j(7 + 5)

= 2 + j12

Question 28

Write down the general example of complex number addition.

Answer 28

z₁ + z₂ = (a + jb) + (c + jd)

= a + jb + c + jd

= (a + c) + j(b + d)

Question 29

Complete the following complex number addition:

(5 + j7) + (3 - j4) - (6 - j3)

Answer 29

(5 + j7) + (3 - j4) - (6 - j3) = 5 +j7 + 3 - j4 - 6 + j3

= (5 + 3 - 6) + j(7 - 4 + 3)

= 2 + j6

Question 30

Write down the general example of complex number multiplication.

Answer 30

z₁ z₂ = (a + jb)(c + jd)

= ac + jad + jbc + j²bd

= ac + jad + jbc - bd

= (ac - bd) + j(ad +bc)

Question 31

Multiply the following complex numbers:

z₁ = 3 + j4

z₂ = 2 + j5

Answer 31

z₁ z₂ = (3 + j4)(2 + j5)

= 6 + j15 + j8 + j²20

= 6 + j23 - 20

= -14 + j23

Question 32

Multiply the following complex numbers:

z₁ = (3 + j4)

z₂ = (2 - j5)

z₃ = (1 - j2)

Answer 32

z₁ z₂ z₃ = (3 + j4)(2 - j5)(1 - j2)

= (3 + j4)(2 - j4 - j5 + j²10)

= (3 + j4)(2 - j9 - 10)

= (3 + j4)(-8 - j9)

= -24 - j27 - j32 - j²36

= -24 - j59 + 36

= 12 - j59

Question 33

Multiply the complex numbers (5 + j8)(5 - j8)

Note: complex conjugates

Answer 33

(5 + j8)(5 - j8) = 25 + j40 - j40 - j²64

= 25 - ( -64)

= 25 + 64

= 89

Question 34

Under what circumstances is the complex number z = a + jb purely real?

Answer 34

The complex number z = a + jb is purely real when b = 0

Question 35

Under what circumstances is the complex number z = a + jb purely imaginary?

Answer 35

The complex number z = a + jb is purely imaginary when a = 0

Question 36

How do you divide one Complex number (z₁ = a + jb) by another (z₂ = c + jd)?

Answer 36

z₁/z₂ = (a + jb) / (c + jd)

to simplify we can make the denominator entirely real using the conjugate complex number z₂*

z₁z₂* / z₂z₂* = (a + jb)(c - jd) / (c + jd)(c - jd)

= ((ac + bd) + j(bc - ad)) / c² + d²

Question 37

What is an Argand Diagram?

Answer 37

An Argand Diagram is a way of visually representing complex numbers.

In an Argand Diagram the complex number is plotted on a pair of co-ordinate axes, where the horizontal axis represents Real numbers and the vertical axis represents Imaginary numbers.

Question 38

Given the modulus (r) and the argument (ø) how can you work out Re(z) and Im(z)?

Answer 38

Given r and ø we can determine Re(z) as follows:

Re(z) = rcos(ø)

Similarly, we can determine Im(z) as follows:

Im(z) = rsin(ø)

Question 39

How would you multiply the following complex numbers:

z₁ = r (cos a + j sin a)

z₂ = s (cos b + j sin b)

hint: use exponential form

Answer 39

z₁ = r (cos a + j sin a)

= re^ja

z₂ = s (cos b + j sin b)

= se^jb

z₁z₂ = re^ja • se^jb

= rs(e^ja • e^jb)

= rs(e^ja+jb)

=rse^j(a+b)

Note: rse^j(a+b) = rs(cos(a+b) + jsin(a+b))

Question 40

What does the polar/exponential formtell us aboutcomplex number multiplication?

hint: magnitudes and angles

Answer 40

The polar form tells us that when we multiply complex numbers we:

• multiply the magnitudes

and

• add the angles
  e. g.

r (cos(a) + jsin(a)) • s (cos(b) + jsin(b))

= rs (cos(a + b) + jsin(a +b))

Question 41

Divide the complex number

z₁ = 7(cos (7π/6) + j sin (7π/6))

by

z₂ = cos (7π/4) + j sin (7π/6)

hint: exp

Answer 41

z₁ = 7(cos (7π/6) + j sin (7π/6))

= 7e^j(7π/6)

and

z₂ = cos (7π/4) + j sin (7π/6)

= e^j(7π/4)

therefore

z₁ / z₂ = 7e^j(7π/6) / e^j(7π/4)

= 7e^j(7π/6) • e^{- j(7π/4)}

= 7e^{j(7π/6 - 7π/4)}

= 7e^{- j7π/12}

z₃ = 7(cos (7π/12) - jsin (7π/12))

Question 42

How would you divide the following complex numbers:

z₁ = r (cos a + j sin a)

by

z₂ = s (cos b + j sin b)

hint: use exponential form

Answer 42

z₁ = r (cos a + j sin a)

= re^ja

and

z₂ = s (cos b + j sin b)

= se^jb

therefore

z₁ / z₂ = re^ja / se^jb

= (r/s)e^ja • e^{- jb}

= (r/s)e^{j(a - b)}

= r/s (cos (a-b) + jsin (a-b))

Question 43

What does the polar/exponential form tell us about complex number division?

hint: magnitudes and angles

Answer 43

The polar form tells us that when we divide complex numbers we:

• divide the magnitudes

and

• subtract the angles
  e. g.

r (cos(a) + jsin(a)) / s (cos(b) + jsin(b))

= r/s (cos(a - b) + jsin(a -b))

Question 44

Does (z₁z₂)* = z₁*z₂* ?

Answer 44

Yes it does.

let z₁ = a + jb and z₂ = c + jd

z₁z₂ = (a + jb)(c + jd)

= (ac - bd) + j(ad + bc)

Therefore:

(z₁z₂)* = (ac - bd) - j(ad + bc)

Given that z₁* = a - jb and z₂* = c - jd

it can be seen that:

z₁*z₂* = (a - jb)(c - jd)

= (ac - bd) + j(-ad -bc)

= (ac - bd) - j(ad + bc)

Thus:

(z₁z₂)* = z₁*z₂*

Question 45

What can we say about zz*?

hint: it something to do with mod z

Answer 45

Given that:

z = a + jb

and

z* = a - jb

we can see that:

zz* = (a + jb)(a - jb)

= a² + b²

Given that |z| = √(a² + b²)

it can be seen that:

zz* = |z|²