Identities for Trigs Flashcards
sec(x)
1/cos(x)
Sine double angle identity: Sin(2x)
2sin(x)cos(x)
Adjacent / Hypotenuse is
cos(θ)
Opposite / Adjacent
tan(θ)
x = arcsec(theta)
sqrt(x^2-a^2)
sin(θ) =
Opposite / Hypotenuse
tan(x) =
sin(x)/cos(x)
cos(x)/1
1/sec(x)
derive: ln(sec(x)+tan(x)) + C
sec(x)
integral: sin(2x)
-1/2cos(2x)+c
csc(x)
1/sin(x)
Opposite / Hypotenuse is
sin(θ)
Hypotenuse / Opposite is
csc(θ)
Tan^2(x) =
Sec^2(x)-1
sec(θ) =
Hypotenuse / Adjacent
integrade: 5^x
(5^x)/ln(5) + c
Reduce sin(x)cos(x) =
1/2sin(2x)
Trapezoidal Rule
Tn = (b-a/2n)*[f(Xo)+2f(x1)+2f(x2)…+2f(xn-1)+f(xn)] ***no coefficient 2 in the first and last terms.

1/cot(x)
tan(x)/1
Simpson’s Rule
Sn = (b-a/3n)*[f(Xo)+4f(x1)+2f(x2)+4f(x3)+2f(x4)….2f(xn-2)+4f(xn-1)+f(xn)] … n must be EVEN integer.

x = arcsin(theta)
sqrt(a^2-x^2)
integral: cos(2x)
1/2sin(2x)+c
1/cos(x)
sec(x)
x = arctan(theta)
sqrt(a^2+x^2)
1/sin(x)
csc(x)
csc(θ) =
Hypotenuse / Opposite
Sin^2(x) =
1-Cos^2(x)
1/n-1(sec^n-2(x))(tan(x)+(n-2/n-1) integral sec^n-2(x) DX
integrade sec^n(x)DX
Hypotenuse / Adjacent is
sec(θ)
cot(x)
1/tan(x)
Cos^2(x) =
1-Sin^2(x)
Derive: tan(x)
sec^2(x)
sin(x)/1
1/csc(x)
Reduce Cos^2(x)
1/2(1+cos(2x))
1+Tan^2(x) =
Sec^2(x)
sqrt(a^2+x^2)
x = arctan(theta)
Sn = (b-a/3n)*[f(Xo)+4f(x1)+2f(x2)+4f(x3)+2f(x4)….2f(xn-2)+4f(xn-1)+f(xn)] … n must be EVEN integer.
Simpson’s Rule
1/sec(x)
cos(x)/1
sqrt(x^2-a^2)
x = arcsec(theta)
tan(θ) =
Opposite / Adjacent
sqrt(a^2-x^2)
x = arcsin(theta)
1/tan(x)
cot(x)
cot(θ) =
Adjacent / Opposite
Reduce Sin^2(x)
1/2(1-cos(2x))
2sin(x)cos(x)
Sine double angle identity: Sin(2x)
tan(x)/1
1/cot(x)
Derive: (5^x)/ln(5)
5^x
sin(x)/cos(x)
tan(x)
integrade: sec^n(x)DX
1/n-1(sec^n-2(x))(tan(x)+(n-2/n-1) integral sec^n-2(x) DX
E = (b-a)^3/12n^2 * M (f’‘(x))

Trapezoidal Error Rule
Tn = (b-a/2n)*[f(Xo)+2f(x1)+2f(x2)…+2f(xn-1)+f(xn)] ***no coefficient 2 in the first and last terms.
Trapezoidal Rule
cos(θ) =
Adjacent / Hypotenuse
1/csc(x)
sin(x)/1
Integral Tan(x)
ln(secx) or -ln(cosx)
integrade: sec(x) DX
ln(sec(x)+tan(x)) + C
integrade: sec^2(x) DX
tan(x) + c
Trapezoidal Error Rule
E = (b-a)^3/12n^2 * M (f’‘(x))
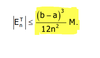
Adjacent / Opposite is
cot(θ)
Simpson’s Error Rule
E = (b-a)^5/180n^4 * M(f’’’‘(x))[4th derivative]

E = (b-a)^5/180n^4 * M(f’’’‘(x))[4th derivative]
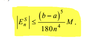
Simpson’s Error Rule
1/2sin(2x)
Reduce sin(x)cos(x) =


