Hyperbolic Functions Flashcards
0
Q
Derivative of sinhx
A
coshx
1
Q
Hyperbolic identities
A
- sinh(-x) = - sinhx
- cosh2(x) - sinh2x = 1
- sinh(x+y) = sinhx.coshy + coshx.sinhy
- cosh(x+y) = coshx.coshy + sinhx.sinhy
- cosh(-x) = coshx
- 1 - tanh2x = sech2x
2
Q
Derivative of coshx
A
sinhx (NOT -sinhx)
3
Q
Derivative of tanhx
A
sech2x
4
Q
Derivative of cschx
A
-cschx.cothx
5
Q
Derivative of sechx
A
-sechx.tanhx
6
Q
Derivative of cothx
A
-csch2x
7
Q
Definition of sinhx
A
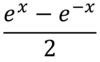
8
Q
Define coshx
A
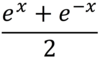
9
Q
Define tanhx
A
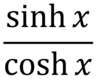
10
Q
Define cosechx
A
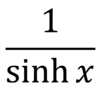
11
Q
Define sechx
A
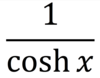
12
Q
Define cothx
A

13
Q
Derivative of sinh-1x
A
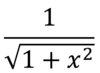
14
Q
Derivative of cosh-1x
A
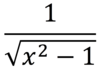
15
Q
Derivative of tanh-1x
A
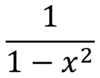
16
Q
Derivative of csch-1x
A
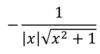
17
Q
Derivative of sech-1x
A
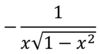
18
Q
Derivative of coth-1x
A
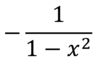
19
Q
Define sinh-1x
A
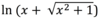
20
Q
Define cosh-1x
A
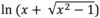
21
Q
Define tanh-1x
A

22
Q
A


