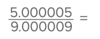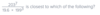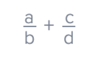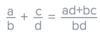Brainscape's Knowledge GenomeTM

Browse over 1 million classes created by top students, professors, publishers, and experts.


See full index

GRE Quant > GRE > Flashcards

GRE Flashcards

You may prefer our related Brainscape-certified flashcards:
GRE® Vocabulary flashcards GRE® Psychology flashcards
1
Q

When both quantities of a QC (Quantitative Comparison) problem are unique values, the answer will never be what?

A

D - cannot be determined

Note: If quantatity A and B are both #’s there will always be a relationship. They will either be equal or one will be greater than the other.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

When both quantities of a QC problem want you to calculate the permiter or the area of bounded figures (shapes), and one of them is a circle, the correct answer will never be what?

A

D

Note: and it is highly unlikely that it will be C

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

What is an improper fraction?

A

numerator > or equal to denominator

i.e. 3/2, 4/3, etc.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

What is a proper fraction?

A

Numerator < Denominator

i.e. 3/4, 3/8, etc.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

Converting an improper fraction to a mixed number.

7/2 = ?

A

3 1/2

Note: divide the num. by the den to get a quotient of 3. Put any remainder over the original den. Remainder of 1 is placed over the 2.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

Converting a mixed # to an improper fraction:

7 2/3 =

A

Multiply the den. by the quotient and add the numerator. Put that all over the original den.

3 x 7 + 2 = 23/3

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

LCD (Least Common Denominator) is what?

A

LCD is the smallest common mutiple of all the denominators in the list.

1/6 = 6, 12, 18, 24, 36, 42, 48, 54, 60

1/5 = 5, 10, 15…55, 60

1/12 = 12, 24, 36, 48, 60

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q

LCD of 1/6, 1/5, and 1/12 = ?

A

60

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

Is 7/56 = 10/80?

A

Yes.

7 x 80 = 560

56 x 10 = 560

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

4/7 + 2/7 = ?

A

6/7

Distributive property of division over addition.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

What is the distributive property of division over addition?

A

A/B = C/B = (A+C)/B

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

4/7 - 1/7 = ?

A

3/7

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

a/b + c/d = ?

Hint: Place in another form

Hint: adding and subtracting with different denominators

A

(ad + bc) / bd

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

a/b - c/d =?

Hint: Place in different form

Hint: adding/subtracting fractions with different denominators.

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q

Division with Fractions

3/4 / 1/7 = ?

Hint: Flip and multiply

A

3/4 * 7/1 = 21/4

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

Multiplication with Fractions and whole #’s

5 x 4/5 =?

A

20/5 = 4

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
17
Q

2/3 / 6 = ?

Hint: flip and multiply

A

2/3 * 1/6 = 2/18 = 1/9

Note: remember to always flip the # that comes after the sign.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
18
Q

The product of a # and its reciprocal is always equal to ??

Hint: 1 over that number

A

Always equal to 1

Note: 4 * 1/4 (Reciprocal) = 4/4 = 1

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
19
Q

What is the only number that does not have a reciprocal?

A

0 is the only number.

Note: any # multiplied by its reciprocal will = 1; however,

0 * 1/0 = 0 and not 1

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
20
Q

Explain 3 ways to reduce fractions

A

1 - multiple all the denominators by the LCD

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
21
Q

How do you find the LCM/LCD using prime factorization?

Hint: LCD - Least Common Denominator and LCM - Least Common Mulitple

A
  1. Prime factor all denominators within the set
  2. Multiply every prime # taking the highest exponent of each prime.
    ex. LCD/LCM (2,5,8) ==> 23 x 51 = 8 x 5 = 40

2 = 21

5 = 51

8 = 23

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
22
Q

More than/ Less than:

is 7/12 > or < 8/12?

A

7/12 < 8/12

Note: In positive fractions with the same denominator, the larger the numerator, the larger the fraction

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
23
Q

Is 3/2 > or < 3/4?

A

3/2 > 3/4

Note: In positive fractions with the same numerator, the larger the denominator, the smaller the fraction and the smaller the denominator, the larger the fraction

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
24
Q

What is the difference between LCM and LCD?

A

LCD is simply used in fraction form because we want the LCM of the denominator.

LCM is a synonymous term for finding the Lowest common multiple of any set of numbers.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
25
Q

T or F:

When adding or subtracting decimal #’s, you want to line up the decimals and fill in the blanks with zeros?

A

True

Always line up the decimals when adding or subtracting

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
26
Q

T or F:

When adding or subtracting decimal #’s, you want to ignore the decimals and complete the addition or subtraction like normal?

A

False.

Always line up the decimals when adding or subtracting numbers

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
27
Q

T or F:

When multiplying decimal #’s, you want to line up the decimals and fill in the blanks with zeros?

A

False.

When multiplying decimals, complete the multiplication like normal, then count the total 3 of decimal places to the right of the decimal, and finally, move the decimal that many places to the left.

.15 x .01 = .0015 (Notice 4 decimal places)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
28
Q

Explain the difference between a dividend and a divisor

I.D. each:

10 dividend by 5

3 over 7

1.2/4

A

Dividend is to the left the sign and the divisor is to the right

10 = dividend, 5 = divisor

3 = dividend, 7 = divisor

1.2 = dividend, 4 = divisor

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
29
Q

Put .0056 in fraction form

A

56/10000

Note:

  1. Remove the decimal and place that number in the denominator
  2. Count the number of decimal places and add that many zero’s to 1
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
30
Q

Rule for squaring and square rooting a number between 0 and 1?

Hint: If x=.776, is X^2 or the SQRT of X greater?

A

Rule: If X is between 0 and 1 (Positive, proper fraction), then X2 < X < SQRT(x)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
31
Q

Which # is larger?

(.99)2 or .(90)2

A

With all positive #’s, including positive fractions, the largest number, when squared, will still be the biggest.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
32
Q

504.132 is about what?

Hint: Estimation/digit properties

A

Answer: about 254,000

32 = 9

500 x 500 = 250,000, but it’s a little bit less.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
33
Q

3 + 8 X 6 =

A

51

Note: Must use PEMDAS. Multiply first, then add

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
34
Q

44 x 87 + 56 x 87 = ?

A

87 ( 44 + 56) =

87 ( 100) =

8700

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
35
Q

Solve:

5 + 10 + 15 + 20……+ 55 + 60

6 + 12 + 18 + 24……+ 66 + 72

Hint: Factor

A

5 ( 1 + 2 + 3 + 4….)

6 ( 1 + 2 + 3 + 4….)

numerator cancels w/ denominator leaving 5/6

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
36
Q

5.0000005/9.0000009 = ?

Hint: Factor

A

5 (1.000001) / 9 (1.000001) = 5/9

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
37
Q

999 + 578 = ?

Hint: Arithmetic Tricks

A

1000 - 1 + 578 =

1578 - 1 = 1577

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
38
Q

0! = ?

A

0! = 1

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
39
Q

1! = ?

A

1! = 1

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
40
Q

If X is between 0 and 1, that is,

0 < X < 1 then what is X is < or > X^2?

Hint: Rule for proper fractions

A

X > X^2

Rule if X is proper fraction:

X^2 < X < SQRTX

X = 1/4

1/16 < 1/4 < 1/2

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
41
Q

If you square a pos. proper fraction, the result is < or > the original?

A

Less than

Rule: X^2 < X < SQRT(x)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
42
Q

List all of the non-negative, single digit int’s:

A

0,1,2,3,4,5,6,7,8,9

Note: Don’t forget zero, dummy.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
43
Q
A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
44
Q
A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
45
Q

Formula for adding a series of consecutive #’s??

Hint: N/2…

A

Ex: 100+101+102+103+104+106+107+108+109+110

N=11

11/2 (100+110) =

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
46
Q

Average of:

100+101+102+103+104+106+107+108+109+110

Hint: Consecutive #’s

A

With consecutive #’s, the average of the set is also the median.

Average = 104

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
47
Q

The opposite of -2 is what?

Hint: Opposite #’s vs. reciprocals

A

The opposits is 2

The opposite of a number, is the number with the opposite sign.

2 = -2

1/4 = -1/4

-14 = 14

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
48
Q

What is the only number that is equal to its opposite?

A

Zero

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
49
Q

What are the only TWO ways any number Y can equal its reciprocal?

Hint: Y = 1/Y

A

If Y = 1 or -1

Dont forget -1

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
50
Q

All fractions (with whole # numerators and denominators) will have either _____ or _____ decimals

A

Terminating or repeating decimals

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
51
Q

If a fraction has a terminating decimal,

the denominator will have factors of only ____ or _____

A

Factors of ONLY 5 or 2

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
52
Q

0! = ?

A

1

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
53
Q

What are the three scenarios that make this statement true: X1+Y!=Z!

A

0! + 0! = 2!

1! + 0! = 2!

1! + 1! = 2!

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
54
Q

When determing the smallest fraction in a set of negative fractions, the fraction that is the most positive will also be the ?

A

Most negative

When wanting to know the smallest fraction between

-5/6 and -6/7, take the most positive fraction and that will also be the most negative.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
55
Q

When the product of two integers is 1, either 1 x 1 = 1, or?

Hint: think negative

A

-1 x -1 = 1

Note: Only two ways the product of two integers can equal 1

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
56
Q

If two things multiply to zero, then atleast one of those things must be equal to ?

A

Zero!

1231231 x 0 = 0

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
57
Q

With any quadratic EQ in fraction form, what cue do you use to factor?

A

Use whatever’s in the denominator as a starting point to help factor.

58
Q

(X+Y)2 = ?

Hint: Quadratic identity

A

(X+Y)2 = X2+Y2+2xy = (x+y)(x+y)

59
Q

(X - Y)2 = ?

A

(X - Y)2 = (X - Y) (X - Y) = X2 + Y2 - 2XY

60
Q

(X + Y) (X - Y) = ?

A

(X + Y) (X - Y) = X2 - Y2

61
Q

X2 - 1 = ?

Hint: Diff of Squares

A

(X - 1) (X + 1)

62
Q

X2 - 9 = ?

Hint: Diff of Squares

A

(X - 3) (X + 3)

63
Q

4X2 - 100 =?

Hint: Difference of Squares

A

(2x - 10) (2x + 10)

64
Q

x2y2 - 16 = ?

Hint: Difference of Squares

A

(xy - 4) (xy + 4)

65
Q

1/36x2 - 25 =?

Hint: Difference of Squares

A

(1/6x - 5) (1/6x + 5)

66
Q

330 - 230 = ?

Hint: Difference of Squares

A

(315)2 - (215)2 = (315 - 215) (315 + 215​)

67
Q

212 - 1 = ?

Hint: Diff of Squares

A

(26 - 1) (26 + 1) = 63 * 65

68
Q

x100 - y100 = ?

A

(x50)2 - (y50)2 = (x50 - y50) (x50 + y50)

69
Q

(5!)2 - (4!)2 = ?

Hint: Diff of squares

A

(5! - 4!) (5! + 4!) = (120 - 24) (120 + 24) = 96 * 144

70
Q

x - y / y - x = ?

A

= -1

This is another way to express -1. Be on the lookout.

71
Q

Hint: # properties

Hint: EQ Trap

A
72
Q

If x and y are pos. int’s. and x ≠ y, when does xy = yx ?

A

x = 2, y = 4 is the only time

24 = 42

16 = 16

73
Q

How do you know if a cubic expression like: ax3 + bx2 + cx + d

can be factored by grouping?

A

You can only factor by grouping if:

a/b = c/d

74
Q

Factor: x3 - 2x2 - 3x + 6

A

= (x-2) (x2 - 3)

75
Q

Factor:

2x3 + 8x2 - x - 4 =

A

(x+4) (2x2 - 1)

76
Q

Find all solutions:

x (x + 100) = 0

A

x = 0

x = -100

IF YOU DIVIDE OUT THE X BY ZERO, YOU WILL MISS THE POSSIBLITY THAT x = 0

77
Q

x2 + .08x - .0048 = 0

find all solutions of x

A

x = -.12, .04

(x - 4/100) (x+ 12/100)

78
Q

x100 - y100 / x50 - y50 =

Hint: Factor

A

(x50)2 - (y50)2 / x50 - y50 = (x50 - y50) (x50 + y50​) / x50 - y50 = x50 + y50

79
Q

(x+2) (6 + 3/x) = 0

How would you solve this?

A
  1. Set each binomial equal to zero

x+2 = 0 6 + 3/x = 0

  1. Solve each for x
80
Q

1 - x2 = ??

Hint: Difference of Squares

A

(1-x) (1+x)

81
Q

If integer Z is divisible by 15 and 20, which of the following is a factor of z?

8, 10, 12, 18, 24, 30

Hint: LCM and Prime Factorization

A

10, 12, and 30

82
Q

Dividend = numerator or denominator?

A

Dividend = Numerator

Divisor = Denominator

83
Q

Divisor = Numerator or denominator?

A

Dividend = Numerator

Divisor = Denominator

84
Q

Any factorial ≥ 5! will always have a units digit of _____?

A

Zero

Due to 5 x 2 pairs

85
Q

The product of any set of N number of intergers is divisible by _____

A

N!

34 x 35 x 36 x 37 x 38 is divisible 5! ( = an integer)

1 x 2 x 3 x 4 is divisible 4! (= an integer)

86
Q

Any integer that is a square root will NOT have units digit of ____?

A

2, 3, 7, or 8

87
Q

The first 11 perfect squares are:

A

0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100

88
Q

Is the product of 3^12 x 2^6 x 7^2 a perfect square?

A

Yes, the prime factorization of a perfect sqaure will only contain even exponents.

89
Q

What are the first nine Perfect Cubes??

A

0, 1, 8, 27, 64, 125, 216, 343, 512

90
Q

Any fraction will have a terminating decimal if ____?

Hint: Prime Factorization

A

The prime factorization of the denominator contains only 2’s or 5’s or both.

91
Q

A perfect square cannot end in _ _ _ or _ .

A

2, 3, 7, or 8

92
Q

SQRT of x2 = ?

A

Absolute value of x

X |

93
Q
A
94
Q

X^2 = 4, X = ?

A

X = |2|

The value of any variable raised to an even exponent will never have a unique value (could be pos./neg.)

95
Q

X^4 = 10000, X = ?

A

X^4 = 10000

10 x 10 x 10 x 10 = 10,000

X = |4|

The value of any variable raised to an even exponent will never have one unique value (could be pos./neg.). **The even exponent masks the sign**

96
Q
A

Rule 1: |a-b| ≥ |a| - |b|

Rule 2: If b ≠ 0, and |a+b| = |a| + |b|, then ‘a’ and ‘b’ have the same sign and |a| ≥ |b|

97
Q

Price per item formula = ?

Hint: Think about it

A

total cost / total # of items = price per item

98
Q

How would you mathmatically write: X increased by y%?

A

X (1 + y/100)

99
Q

How would you mathamtically write: “The item’s cost (x) increased by 50%”

A

= x (1 + 50/100)

= x (1 + 1/2)

= x (3/2)

= 3x/2

100
Q

Profit equation = ?

A

Profit = Total revenue - Total cost

101
Q

Translate to EQ:

If 55 were added to X, Y would be 1/6 of this new value

A

(1/6) X + 55 = Y

102
Q

Translate to two equations:

A certain store purchases milk for Y dollars per gallon and sells it for X dollars per gallon. The store marks up every gallon of milk that it sells by 50%, and x + y = 12.

A

1) x + y = 12
2) x = 1.5y

103
Q

Create equation:

If you add 7 to molly’s age and 3 to holly’s age the ratio of their ages would be 5:3

A

M + 7 = 5

H + 3 = 3

104
Q

Distance Formula =?

A

Distance = Rate x Time

105
Q

Time Formula = ?

Hint: Rate Forumla

A

Time = Distance/Rate

106
Q

Rate Forumla = ?

A

Rate = Distance/Time

107
Q

Catch up and Pass formula = ?

A

Time = Change in D/ Change in Time

108
Q

What do you do when ask to combine rates?

A

Add rate1 and rate2

109
Q

When two objects work together….

A

Workobject 1 + Workobject 2 = WorkTotal

Find work of both respective objects and set equal to one

110
Q

If |m + n| = |m| + |n|, then what do we know about it?

A

We know that either m or n is 0, or they have the same signs

111
Q

Practice Time!

A

Go take Module 9-12 Review Test

112
Q

Practice Time!

A

Go take

Review Quiz #9

113
Q

Put 25 x 1012 in Scientific notation

A
  1. 5 x 1013
  2. As the number in front of the ‘X’ increases, the power of 10 decreases.
  3. As the # in front of the ‘X’ decreases, the power of 10 increases
114
Q

Put 25 x 1012 in Scientific notation

A
  1. 5 x 1013
  2. As the number in front of the ‘X’ increases, the power of 10 decreases.
  3. As the # in front of the ‘X’ decreases, the power of 10 increases
115
Q

Direct Variation EQ = ?

Be on the lookout for “Direct Variation”. Problems will say something like, “proportions vary directly” or “the mileage is inversely proportional”.

A

Y = KX

116
Q

Inverse Variation EQ = ?

Be on the lookout for “Direct Variation”. Problems will say something like, “proportions vary directly” or “the mileage is inversely proportional”.

A

y = k/x or yx = k

117
Q

Percent Less than Formula = ?

A

Final/New Value = Initial Value * [1 - (“% less than”/100)]

118
Q

The percent of .5 that is 2

A

This means, “2 is what percent of .5”?

119
Q

The percent of 2 that is .5

A

This means, “.5 is what percent of 2”?

120
Q
A

Solution = (1.4)5 * 100,000

Notes - “5” is the number of years

4any odd # = a units digit ending in 4

121
Q

Formular for Either A or B = ?

A

(A or B) = #A + #B - (Both A and B)

122
Q

Average Formula =

A

Sum of all items/ # of items

123
Q

Sum of all terms =

A

of terms * average

124
Q

How many #’s are in the set 50-100 inclusive?

Hint: Counting both of the endpoints

A

100 - 50 + 1 = 51

When counting consecutive integers in a set that includes the first and last numbers (Inclusive), calculate by using:

Highest # - Lowest # + 1 = Total

125
Q

of multiples of 3 between 17-41, inclusive?

A

(39-18/3) + 1 = 8

126
Q

Sara is 50th and Tom is 10th. How many people are there from Tom to Sara, including Tom, but not Sara?

Hint: Counting only one of the endpoints.

A

50 - 10 = 40 people

High # - Low # = Total

127
Q

Hint: counting the # between two #’s. Counting neither of the endpoints

A
128
Q

What is the average of 100, 200, 300, 400, and 500?

Hint: Quick average for even spaced #’s

A

(500 + 100) / 2 = 300

( H + L ) / 2 = Avg

*Can only be used with evenly spaced #’s*

129
Q

Average formula for evenly spaced sets of #’s?

A

Highest # + Lowest number / 2

130
Q

Using the average formula to find the sum of a set of evenly spaced numbers = ?

A

Sum = Avg * Total #’s in set

Avg = H + L / 2

Total # = Consecutive Int Formulas

131
Q

Weighted Average formula = ?

A

WA = Sum of weighted terms (a * x) + (b * y) / Total number of weighted terms ( a + b)

132
Q

Position of median formula with an odd number of terms =?

A

Position of median = (N + 1) / 2

N = Total # of terms

133
Q

What is the average of all the multiples of four, between 1 and 100 inclusive?

A

avg = (4 + 100)/ 2 = 52

  1. In this case the highest and lowest multiple’s of 4 are 4 and 100.
  2. Add the highest and lowest multiple’s of 4 that fit within the parameters of 1- 100).
  3. Divide the sum of these two ints. By two to get the average of the whole set.
134
Q

Fundamental Counting Principal

A
135
Q

Combinations Formula

Hint: N choose K

A

nCk = n! / k! (n-k)!

N = total objects

K = # of objects selected

136
Q

a) 1! = ?
b) 0! = ?

A

a) 1
b) 1

137
Q

21!/ 3 = how many 3’s ??

hint: the # of prime factors in a particular factorial

A

21/31 = 21/3 = 7

21/32 = 21/9 = 2 + remainder

7+2 = 9 3’s

**must make sure that the denominator is prime factored**

138
Q

What is the largest # that must be a factor of the product of any four consecutive positive integers?

a) 6
b) 12
c) 24
d) 30
e) 48

Hint: Division props of factorials

A

N consecutive integers must de divisible by N!

4 consecutive integers must be divisible by 4!

4 x 3 x 2 x 1 = 24

139
Q

When will a fraction have a terminating decimal?

A

A fraction will terminate when the denominator of the reduced fraction contains only 2’s, 5’s, or both 2’s and 5’s and nothing else.

140
Q

The remainder when 2,179,997 is divided by 5?

A

When dividing by 5, the remainder will always be the units over 5.

7/5 = Q r2

GRE Quant (1 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2024 Bold Learning Solutions. Terms and Conditions