Gravitational fields Flashcards
Gravitational fields
Define a gravitational field
A field is a region in which a force may be exerted by an object.
What are the rules for drawing gravitational field lines?
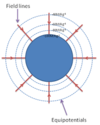
Gravitational Field lines represent the direction of force on a mass at a point.
The separation between fields lines represents their strength Field lines drawn for a single mass (gravitational or otherwise) never cross each other.
Gravitational field lines always point towards the centre of mass. (Gravitational force is always attractive).
Define the strength of a gravitational field (g)
The force per unit mass on a small test mass placed in the field.
Describe a radial field
The field lines are like the spokes of a wheel, towards the centre.
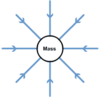
What happens to g in a radial field?
Decreases with increasing distance from the massive body.
Describe a uniform field
Field lines are parallel and equally spaced.
What happens to g in a uniform field?
Magnitude and direction of g is constant.
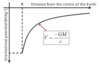
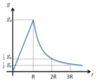
Sketch a graph of gravitational field strength against separation.
State what can be calculated from this graph
See diagram
Area = Gravitational potential
Explain why mass of an object is constant but weight may change
- Mass only depends on the number of particles present.
- Weight is a force which depends on gravitational field strength
- Gravitational fields strength varies on every planet
Define Newton’s law of gravitation?
Attractive force
Proportional to the mass of each object
Inversley Proportional to r2 (r is distance between objects)
When using Newtons law of atteaction equation why can planets be assumed to be point masses?
The diamater of a planet is much smaller than the distance between the two planets.
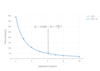
Sketch a graph of force against separation.
State what can be found from this graph
See diagram
Area = work done = GPE
State Kepler’s first law
The orbital path of a planet around the Sun is an ellipse, not a perfect circle. The Sun lies at one of the foci of the ellipse
State Kepler’s second law
An imaginary line connecting the Sun to any planet sweeps out equal areas of the ellipse over equal intervals of time.
KE + PE = a constant
If the radius of a orbit decreases what happens to the speed, kinetic energy, potential energy and total energy?
Total energy is constant
Total energy = kinetic + potential
Potential energy - decreases so
Kinetic energy and speed increases
If the radius of a orbit increases what happens to the speed, kinetic energy, potential energy and total energy?
Total energy is constant
Total energy = kinetic + potential
Potential energy - increases so
Kinetic energy and speed decreases
What is Kepler’s Third Law?
The period of planet’s orbit squared is proportional to the cube of the average radius of its orbit.
T2 proportional r3
State the equations needed to derive the orbital velocity equation
F = mv2/r and
F = GM1M2/r2
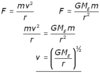
State the equations needed to derive the orbital time period equation equation (Keplers 3rd Law)
F = mv2/r and
F = GM1M2/r2 and
v = 2πr/T
State the orbital time period for a geostationary satellite
24 hours
State the criteria for a geostationary orbit
- Have a time period of 24 hours
- Be at a height of 36 000 km above the Earths surface
- Be circular
- Be equatorial (in the plane of the equator)
- Rotate in the same direction of the earth (west to east)
State some benefits of a polar (low) orbit
- A cheaper launch cost
- Eventually cover the whole earth as the satellite doesn’t stay above the same point
Define gravitational potential energy
The gravitational potential energy (W) at a point in a field, is the work done to move an object from infinity to that point.
It is measured in joules
State the equation for gravitational potential energy
Ep = - GMm / r
Sketch a graph of GPE against separation. What can be found from this graph?
see diagram
Gradient = force
Sketch a graph of GPE against seperation for a journey from the Earth to the Moon.
See diagram.
Define gravitational potential
Gravitational potential at a point is the work done per unit mass to move a small object from infinity to that point.
It is measured in Jkg-1
Is gravitational potential a vector or scalar?
Scalar
Why is gravitational potential always negative?
GPE is zero at infinity.
The further you raise the object, the more work you do and the greater the change in gpe.
GPE increase with distance but can only increase to 0 at infinity.
Sketch a graph of gravitational potential against separation.
What can be found from this graph?
see diagram
Gradient = g
Define potential gradient (gravitational)
Potential gradient at a point in a gravitational field is the change in potential per metre at that point.
How are gravitational potential and gravitational potential energy related?
V = W/m
Potential is the work done per unit mass.
V - Gravitational potential (J/kg)
W - GPE (J) m - mass (kg)
What are equipotentials?
surfaces that join up points of equal potential.
Sketch the lines of equipotential in a uniform field.
They are horizontal lines, perpendicular to the gravitational field lines.
They are evenly spaced.
Sketch the lines of equipotential in a uniform field.
Circular rings around the planet.
Spacing of lines of equipotential increases as seperation increases
Is work done when a mass moves along a line of equipotential?
No as no change in potential and
W = change in potential x mass
What is shown when lines of equipotential are close together?
If the equipotential are close together, a lot of work must be done over a relatively short distance to move a mass from one point to another against the field – i.e. the field is very strong.
Why does the spacing between lines of equipotential increase as the seperation from the planet increases?
This shows that the potential changes more rapidly for changes in height near the Earth than for changes of height a long distance away from the Earth.
Potential gradient = gravitational field strength, g.
State the direction between lines of euipotential and gravitational field lines
Lines of equipotential must be at right angles to gravitational field lines.
The arrow on gravitational field lines points towards the centre of mass so in the direction of increasing potential.
Define escape velocity
The minimum velocity an object must be given to escape from the planet when projected vertically from the surface.
For this to happen, the kinetic energy of the mass must be equal to the GPE gained
What is the formula to remember for escape veloctiy?
Vesc = (2gr)0.5
g is gravitational field strength
r is the radius of the planet
How can you derive the escape velocity equation?
Initial Kinetic energy = gain in GPE
once object has escpape gravitational field GPE = 0
so
0.5mv2 = GMm/r
State two reasons why rockets launched from Earth do not need to achieve escape velocity to reach their orbit?
- Energy continually added in flight by thrust provided by fuel
- Less energy is need to achieve orbit rather than escaping Earth’s gravitational field
Why is the total energy supplied by a fuel to launch a satellite greater than the change in potential energy of the satellite?
- Energy lost to friction (heat) and sound
- Combustion of fuel is not 100% efficient (light wasted)
- Satellite given KE and PE as it moves upwards
- Fuel given some KE as ejected downwards
- Fuel is needed to raise the height of the fuel, rocket and satellite combined
