Graphs Flashcards
(16 cards)
What is a graph?
It’s an abstraction to represent connectivity between objects Formally an undirected graph G it a collection of vertices V and edges E between pairs of them.
What is a loop in a graph? What is a simple graph?
It’s a path which connects a vertex to itself. A simple graph is a graph with no loops.
Describe ways to represent graphs in computer and compare their performance
- Edge list 2. Adjacency matrix 3. Adjacency list

Let’s say we have a graph G and a vertice s. How to find all vertices v in G such that there is a path from s to v?

What is an idea of DFS? Runtime?
O(|E|) + O(|V|)
Each vertex is marked as visited exactly once - O(1) work per vertex
Each vertex checks each neighbour and total number of neighbours in O(|E|)

What is a connected component in an undirected graph?
It’s a set of vertices of a G, such that v is reachable from w if and only if they are in a same connected component.
How to find connected components in an undirected graph?
Use the modification of DFS with markers for connected components

What is a DAG?
A directed acyclic graph is a directed graph G without cycles.
What directed graphs can be linearly ordered?
Any DAG can be linearly ordered. A graph with a cycle can not be.
What are strongly connected components in a DAG?
The vertices v and w in a DAG G are connected if you can reach v from w and w from v. A DAG can be partitioned into strongly connected components where two vertices are connected iff they are in the same cmponents
What is a metagraph? What properties it has?
It’s a graph describing connectivity between strongly connected coponents. A metagraph is a always a DAG.
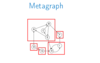
What are sources/sinks?
A source is a vertex with no incoming edges, and a sink is a vertex with no outgoing edges.
How to do a topological sort of a DAG?
- DFS(G)
- sort vertices by reverse post-order
How to compute strongly connected components of a DAG?

What is the idea behind computig strongly connected components?
Idea: If v is in a sink SCC, explore(v) nds vertices reachable from v. This is exactly the SCC of v.
The vertex with the largest postorder number is in a source component!
Find sink components of G by running DFS on G R
Don’t need to rerun DFS on G R . Largest remaining post number comes from sink component.
Runtime O(|V | + |E|)
What are main ideas of Dijkstra’s algorithm?



