GMAT 01 - Fractions & Decimals Flashcards
3/8 + 1/2 = ?
LCD = 8
= 7/8
3 + 1/4 = ?
3 + 1/4 = 3 1/4
= 13/4
Fractions within the Denominator trick
Fractions that contain a fraction in the denominator can be simplified by putting the numerator over one and multiplying the numerator by the “flip” of the denominator
example:
2/(1/3)
= (2/1) / (1/3)
= (2/1) x (3/1)
= 6
5/7 - 1/3 = ?
LCD = 21
= 8/21
Simplify the Fraction:
75/300
= 1/4
( 75/300 = (3x25) / (3x100) = 25/100 )
( 25/100 = (1x25) / (4x25) = 1/4 )
This fraction breaks down twice
How do you convert a fraction into a mixed numeral?
1) Divide the numerator by the denominator. The number of times that the denominator can go into the numerator determines the whole number portion of the mixed numeral
2) Place the remainder over the denominator. The resulting fraction is the fractional portion of the mixed numeral.
5/7 - 2/7 = ?
= 3/7
(y/4) / (y/x) = ?
= x/4
(y/4) / (y/x) = (y/4) x (x/y)
(y’s eliminate)
= (1/4) x (x/1)
= x/4
(2a/3b) / 2ac = ?
= 1/3bc
(2a/3b) / 2ac
= (2a/3b) / (2ac/1)
= (2a/3b) x (1/2ac)
= 2a/6abc
= 1/3bc
3 3/4 x 7 1/3 = ?
= 55/2
3 3/4 x 7 1/3
= (12/4)+(3/4) x (21/3)+(1/3)
= 15/4 x 22/3
(common denominator = 4x3 = 12)
6 / (4x-x) = ?
= 2/x
6 / (4x-x)
= (2)(3) / (3x)
= 2/x
X - 1/4 = ?
LCD = 4
= (4x-1)/4
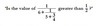
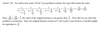
1/5 + 2/5 =
= 3/5
(ab2c)/(abc) x (ac)/(abc) = ?
= 1
(ab2c)/(abc) x (ac)/(abc)
= b(abc)/(abc) x (ac)/(abc)
= (b)/1 x (ac)/abc)
= abc/abc
= 1
4 - 1/5 = ?
LCD = 5
= 19/5
14/9 x 6/21 = ?
= 4/9
14/9 x 6/21 = (2x7)/(3x3) x (3x2)/(3x7)
7s and one set of 3s cancel
= (2/3) x (2/3)
= 4/9
6 + 2/x = ?
6 + 2/x = 6 2/x = (6x + 2) / x
Simplify the Fraction:
14/98
= 1/7
( 14/98 = (2x7) / (2x49) = 7/49 )
( 7/49 = (1x7) / (7x7) = 1/7 )
This fraction breaks down twice
7 1/4 - 4 1/2 = ?
= 11/4
7 1/4 - 4 1/2
= (28/4)+(1/4) - (8/2)+(1/2)
= 29/4 - 9/2
(common denominator = 4)
29/4 - (2/2)(9/2)
= 29/4 - 18/4
= 11/4
Fractions within the Numerator Trick
Fractions that contain a fraction in the numerator can be simplified by putting the denominator over one and multiplying the numerator by the “flip” of the denominator
Example:
(2/3)/4
= (2/3) / (4/1)
= (2/3) x (1/4)
= 2/12
= 1/6
Convert into a Mixed Fraction:
38/7
= 5 3/7
( 38/7 = 5 remainder 3)
Convert into a Mixed Fraction:
25/4
= 6 1/4
(25/4 = 6 remainder 1)
(11-1) / (2+3) = ?
= 2
(11-1) / (2+3)
= 10/5
= 2
How do you add fractions with different denominators?
To add fractions with different denominators
1) first you must ffind the lowest common denominator (LCD)
2) then you must convert each fraction to be added into a new fraction by multiplying the numerator and the denominator of each fraction by the value that raises each denominator to the LCD.
This process is known as converting fractions to equivalent fractions
Simplify the Fraction:
24x4y3/18x2y2
= 4x2y/3
( 24x4y3/18x2y2 = {(4x2y)(6x2y2)} / (3)(6x2y2) = 4x2y/3 )
The 6x2y2s cancel out
If the numerator of a fraction is zero
The value of the fraction is zero
(1+2) / 6 = ?
= 1/2
(1+2) / 6
= 3/6
= 1/2
How do you simplify a fraction that contains a fraction within its numerator and/or denominator?
To simplify a fraction that contains a fraction within its numerator and/or denominator, always multiply the numerator by the “flip” of the denominator.
example =
(2/5) / (1/3)
= (2/5) x (3/1)
= 6/5
How do you subtract whole numbers and fractions from one another?
To subtract whole numbers and fractions from one another:
a) place the whole number over 1
b) find the LCD between the whole number and the fraction
c) convert the numbers to a shared denominator
d) subtract one number from the other
X + 4/5 = ?
X + 4/5 = X 4/5 = (5x + 4)/5
Definition: Reciprocals
Reciprocals are any two numbers whose product equals 1.
>> While commonly thought of as “flips” that there are also reciprocals that assume different forms – in particular, look to reciprocals involving roots <<
It is also important to remember that a fraction may have more than one reciprocal
>> To determine whether two numbers are reciprocals, always multiply them together <<
Simplify the Fraction:
700/28
= 25
( 700/28 = (7x100) / (7x4) = 100/4 )
( 100/4 = (25x4) / (4x1) = 25)
This fraction factors twice
12/(2/5) = ?
= 30
12/(2/5)
= (12/1) x (5/2)
= 60/2
= 30
(Y/4) x (Y/X) = ?
= Y2/4X
(Y/4) x (Y/X) = (YxY) x (4X)
= Y2/4X
Rule: Working with Mixed Numerals
When working with mixed numerals, always convert the mixed numerals into fractions before adding, subtracting, multiplying, or dividing.
How to express a whole number as a fraction
Set the whole number as a fraction over 1
What is the reciprocal of k + (g/x), where k+(g/x) does not = 0?
= x/(kx+g)
k + (g/x)
= (k/1)(x/x) + (g/x)
= (kx + g)/x
Reciprocal = x/(kx + g)
5 + 2/3 = ?
5 + 2/3 = 5 2/3
= 17/3
(173 + 172) / (172) = ?
= 18
<< Complex Numerator Shortcut>>
(173 + 172) / (172)
= (173/172) + (172/172)
= (17/1) + 1
= 18
15/100 x 45 = ?
= 27/4
15/100 x 45 = (5x3)/(4x5x5) x (3x3x5)/1
= 3/4 x (3x3)
= 27/4
(282 + 28) / 28 = ?
= 29
<< Complex Numerator Shortcut>>
(282 + 28) / 28
= (282/28) + (28/28)
= (28/1) + 1
= 29
In which of the following pairs are the two numbers reciprocals?
a) 2/5 and 5/2
b) (root 5/2) and (2 root 5/5)
c) (root 5/2) and (2/root 5)
= a, b, and c
all options = 1
(2 3/4) / (5 1/2) = ?
= 1/2
(2 3/4) / (5 1/2)
= (8/4)+(3/4) / (10/2)+(1/2)
= (11/4) / (11/2)
= (11/4) x (2/11)
(eliminate 11s)
= 2/4
= 1/2
(4x-x) / (2x+7x) = ?
= 1/3
(4x-x) / (2x+7x)
= 3x/9x
= (3/3) (x/3x)
= 1/3
The Complex Numerator Shortcut
In complex fractions, if the numerator of a fraction contains addition or subtraction, that fraction can be split to simplify the arithmetic.
example:
(282 + 28) / 28 = (282/28) + (28/28)
= 28/1 + 1
= 29
This CANNOT be done with a complex denominator!
(a/b) / (c/d) = ?
= (ad)/(bc)
(a/b) / (c/d)
= (a/b) x (d/c)
= (ad)/(bc)
(5/80) / (2/24) = ?
= 3/4
(5/80) / (2/24)
= (5/5)(1/16) / (2/2)(1/12)
= (1/16) / (1/12)
= (1/16) x (12/1)
= 12/16
= (4/4)(3/4)
= 3/4
(y-x) / (x) = ?
= (y/x) - 1
<< Complex Numerator Shortcut >>
(y-x) / (x)
= (y/x) - (x/x)
= (y/x) - 1
How do you multiply fractions?
To multiply fractions:
1) multiply the numerators together
2) then multiply the denominators together
To save time, be sure to rip up the numerators and denominators by factoring and canceling out the common terms.
1/y + y/3 = ?
LCD = 3y
(3 + y2)/3y
Simplify the Fraction:
6/8
= 3/4
( 6/8 = (2x3) / (2x4) = 3/4 )
(the 2s cancel)
Simplify the Fraction:
900/18
= 50
( 900/18 = (9x100) / (9x2) = 100/2 )
( 100/2 = (2x50) / (2x1) = 50 )
This fraction factors twice
Definition of a Fraction
A fraction is a number in the form a/b, where a andb are integers and b does not equal zero
(x/y) / (1/5) = ?
= 5x/y
(x/y) / (1/5) = (x/y) x (5/1)
= 5x/y
x + (y/z) = ?
x + (y/z) = x (y/z)
= (xz + y)/z
7/x + 5/x = ?
= 12/x
How do you divide a fraction by a fraction?
To divide a fraction by another fraction, flip/invert the second fraction (the divider) and multiply it by the first fraction
ex. (1/4) / (2/5) = (1/4) x (5/2)
= 5/8
Definition: Complex Fraction
A complex fraction is any fraction that contains addition or subtraction in either the numerator or the denominator.
To simplify complex fractions, you must carry out the addition or subtraction in the numerator and/or denominator before simplifying the resulting fraction
>> Terms can only be cancelled within simple fractions <<
(you cannot factor out from the top and bottom if that factor only applies to one figure within the complex element of the fraction)
7-(2/x) = ?
LCD = x
= (7x-2)/x
How do you add whole numbers and fractions?
To add whole numbers and fractions:
1) combine the two numbers into a mixed numeral
2) convert the mixed numeral into a single fraction
Definition: the number on top of a fraction
The Numerator
(2a/3) / (4b/3) = ?
= a/2b
(2a/3) / (4b/3)
= (2a/3) x (3/4b)
= 6a/12b
= a/2b
(a+b)/b = ?
= (a/b) + 1
<< Complex Numerator Shortcut>>
(a+b)/b
= (a/b) + (b/b)
= (a/b) + 1
Simplify (3 1/2 x 1 1/4) + [(1 5/4) / (2/5)}
= 10
(3 1/2 x 1 1/4) + [(1 5/4) / (2/5)}
= {(6/2 + 1/2) x (4/4 + 1/4)} + {(4/4 + 5/4) / (2/5)}
= (7/2)(5/4) + {(9/4)/(2/5)}
= (35/8) + {(9/4) x (5/2)}
= (35/8) + (45/8)
= 80/8
= 10
(2/xy) - (x/xy) = ?
= (2-x)/xy
If the denominator of a fraction is zero
the fraction is undefined (has no answer)
Convert into a Mixed Fraction:
17/7
= 2 3/7
(17/7 = 2 remainder 3)
3/7 - 1/9 = ?
LCD = 63
= 20/63
Simplify the Fraction:
24/64
= 3/8
( 24/64 = (3x8) / (8x8) = 3/8 )
(One 8 from each expression cancels)
(77/14) / (22/30) = ?
= 15/2
<< Always factor first – it saves a lot of time >>
(77/14) / (22/30)
= (7/7)(11/2) / (2/2)(11/15)
= (11/2) / (11/15)
= (11/2) x (15/11)
(11’s eliminate)
= 15/2
14/3 x 3/7 = ?
= 2
14/3 x 3/7 = (2x7)/3 x (3/7)
3s and 7s cancel
= 2
14a/(2/b) = ?
= 7ab
14a/(2/b)
= (14a/1) (b/2)
= 14ab/2
= 7ab
(y/x) / (y/x) = ?
= 1
(y/x) / (y/x) = (y/x) x (x/y)
= YX/XY
(all variables eliminate)
= 1
Convert into a Mixed Fraction:
18/5
= 3 3/5
( 18/5 = 3 remainder 3)
(36/5) / 24 = ?
= 3/10
(36/5) / 24
= (36/5) / (24/1)
= (36/5) x (1/24)
= 36/120
= (12/12)(3/10)
= 3/10
2/(1/3) = ?
= 6
2/(1/3)
= (2/1) / (1/3)
= (2/1) x (3/1)
= 6
Any number express as a fraction can also be understood as
the result of dividing the numerator by the denominator (which has a decimal equivalent)
How do you add two fractions with a common denominator?
Two fractions with a common denominator can be added or subtracted by adding or subtracting the numerators, while leaving the denominators the same
Find the reciprocal
(1/5) - x
= 5/(1-5x)
= (1/5) - (5/5)(x/1)
= (1/5) = (5x/5)
= (1-5x)/5
reciprocal = 5/(1-5x)
x/5 + x/3 = ?
LCD = 15
= 8x/15
What is the value of (2 1/3 + 1 3/4) / (2 5/6 - 1 1/2) ?
= 49/16
(2 1/3 + 1 3/4) / (2 5/6 - 1 1/2)
= (6/3+1/3 + 4/4+3/4) / (12/6+5/6 - 2/2+1/2)
= (7/3 + 7/4) / (17/6 - 3/2)
(common denominators = 3x4 = 12 and 6)
= {(4/4)(7/3) + (3/3)(7/4)} / {(17/6) - (3/3)(3/2)}
= (28/12 + 21/12) / (17/6 - 9/6)
= (49/12) / (8/6)
= (49/12) x (6/8)
= (49x6) / (12x8)
= (49x6) / (2x6x8)
(eliminate 6’s)
= 49/(2x8)
= 49/16
(4/9) / (4/5) = ?
= 5/9
(4/9) / (4/5)
= (4/9) x (5/4)
= 20/36
= (4x5) / (4x9)
eliminate 4’s
= 5/9
1/2 x 3/4 = ?
= 3/8
1/2 x 3/4 = (1x3) / (2x4) = 3/8
Convert into a Mixed Fraction:
20/3
= 6 2/3
(20/3 = 6 remainder 2)
(13/68) / (52/17) = ?
= 1/16
(13/68) / (52/17)
= (13/68) x (17/52)
= (1/17)(13/4) x (1/13)(17/4)
= (13x1)/(17x4) x (17x1)(13x4)
(eliminate 17’s and 13’s)
= (1/4) x (1/4)
= 1/16
How do you simplify a fraction?
To simplify any fraction, factor the numerator and denominator and cancel out all common terms.
(2/3)/4 = ?
= 1/6
(2/3)/4
= (2/3) / (4/1)
= (2/3) x (1/4)
= 2/12
= 1/6
How do you convert a mixed numeral into a fraction?
1) Multiply the denominator by the whole number and add the numerator
2) Place the sum over the denominator
Definition: Levels of Fractions
Complex Fractions that contain fractions in either the numerator or the denominator can be thought of as having multiple “levels.”
Each “level” typically consists of two terms that need to be added or subtracted.
>> To simplify such fractions, work one “level” at a time, starting with the bottom “level” and progressing upwards <<
Example:
1/(2 + 1/3)
= 1/(2 1/3)
= (1/1) / (7/3)
= (1/1) x (3/7)
= 3/7
Convert into a Mixed Fraction:
40/3
= 13 1/3
(40/3 = 33 remainder 1)
(1/2) / (4/3) = ?
= 3/8
(1/2) / (4/3) = (1/2) x (3/4)
= (1x3) / (2x4)
= 3/8
(2/3) / (7/5) = ?
= 10/21
(2/3) / (7/5) = (2/3) x (5/7)
= (2x5) / (3x7)
= 10/21
What is the value of (3 - 1/3) - (5 - 1/5) ?
= -32/15
(3 - 1/3) - (5 - 1/5) = (9/3 - 1/3) - (25/5 - 1/5)
= 8/3 - 24/5 = 40/15 - 72/15
= 32/15
Simplify the Fraction:
35/42
= 5/6
( 35/42 = (7x5) / (7x6) = 5/6 )
(the 7s cancel)
(2/5) / (1/3) = ?
= 6/5
(2/5) / (1/3)
= (2/5) x (3/1)
= 6/5
b/(b/a) = ?
= a
b/(b/a)
= (b/1) (a/b)
= a
35 x 42/98 = ?
= 15
35 x 42/98 = (5x7)/1 x (2x3x7)/(2x7x7)
7s and 2s cancel
= (5x3)
= 15
1 + x/3 = ?
1 + x/3 = 1 x/3
= (3 +x)/3
1/2 + 2/3 = ?
LCD = 6
1/2 + 2/3 = 3/6 + 4/6 = 7/6
Simplify the Fraction:
XY2/ X2Y
= Y/X
( XY2/ X2Y = (Y(XY)) / (X(XY)) = Y/X)
The XYs cancel
5 - 2/3 = ?
LCD = 3
= 13/3
x/5 x 2/3 = ?
= 2x/15
x/5 x 2/3 = (2x) / (3x5)
= 2x/15
Definition: the number on the bottom of a fraction
The denominator
(eg. the fraction 2/3 has a denominator of 3)
1 1/5 + 3 1/3 = ?
= 68/15
1 1/5 + 3 1/3
= (5/5)+(1/5) + (9/3)+(1/3)
= 6/5 + 10/3
(common denominator = 5x3 = 15)
(3/3)(6/5) + (5/5)(10/3)
= (18/15) + (50/15)
= (18+50)/15
= 68/15
(4/30) / (12/105) = ?
= 7/6
(4/30) / (12/105)
= (2/2)(2/15) / (3/3)(4/35)
= (2/15) / (4/35)
= (2/15) x (35/4)
= (2x35) / (15x4)
(divide by 2/2)
= (1x35) / (15x2)
= 35/30
= 5x7)/ (5x6)
= 7/6
2/3 x 5/7 = ?
= 10/21
2/3 x 5/7 = (2x5) / (3x7)
= 10/21
What is the value of (2 + 4/5) - (3 + 4/7) ?
= -27/35
(2 + 4/5) - (3 + 4/7) = 14/5 - 25/7
= 98/35 - 125/35
= 27/35
(6/b) / 2 = ?
= 3/b
(6/b) / 2
= (6/b) / (2/1)
= (6/b) x (1/2)
= 6/2b
= 3/b
Definition: Simple Fraction
A simple fraction contains no addition or subtraction in either the numerator or the denominator
>> Terms can only be cancelled within simple fractions<<
(you cannot factor out from the top and bottom if that factor only applies to one figure within the complex element of the fraction)
Simplify the Fraction:
7/21
= 1/3
( 7/21 = (1x7) / (3x7) = 1/3 )
(the 7s cancel)
Definition: Mixed Numeral
A Mixed Numeral is the combination of a whole number and a fraction
(3x2/2XY) x (21Y/6X) = ?
= 21/4
(3x2/2XY) x (21Y/6X) = (3)(x)(x)/(2)(x)(y) x (3)(7)(y)/(2)(3)(x)
= (3x)/(2y) x (7y)/(2x)
= (3x7)/(2x2)
= 21/4
(x/5) / (3/2) = ?
= 2x/15
(x/5) / (3/2) = (x/5) x (2/3)
= (2x) x (5x3)
= 2x/15
Find the reciprocal
y + (1/x) = ?
= x/(xy+1)
y + (1/x)
= (y/1) + (1/x)
= (x/x)(y/1) + (1/x)
= (xy/x) + (1/x)
= (xy+1)/x
Reciprocal = x/(xy+1)
