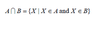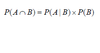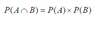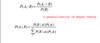Brainscape's Knowledge GenomeTM

Browse over 1 million classes created by top students, professors, publishers, and experts.


See full index

Stats Test 1 - "It's all intuitive." > General Probability Theory > Flashcards

General Probability Theory Flashcards

1
Q

What is a a sample?

A

A subset that is drawn from a larger population i.e. r<n></n>

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

What is a parameter?

A

Something in the population that we want to estimate.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

Why do we do statistics?

A

To deliver us an estimate of a specific (numerical) parameter in the population based on the information obtained in a sample.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

What are the two basic types of statistics?

A

Descriptive and Inferential

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

What is descriptive statistics?

A

It is the DESCRIPTION of characteristics of a set of numbers (e.g. mean, variance, etc.)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

What is inferential statistics?

A

They attempt TO INFER (deduce or conclude (information) from evidence and reasoning rather than from explicit statements) i.e. they are used to estimate a population parameter from a SAMPLE STATISTIC – going back from the sample to infer something about the population

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

Statistical Inference is based upon what?

A

PROBABILITY

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q

What is a fundamental concept in scientific research that is linked with probability?

A

Determining the likelihood of some event occurring in nature.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

What is a key assumption or goal of probability?

A

“The theory of chance consists in reducing all the events of the same kind to a certain number of cases equally possible, that is to say, to such as we may be equally undecided about in regard to their existence, and in determining the number of cases favorable to the event whose probability is sought.” – Pierre-Simon Laplace

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

What is a random selection?

A

It is a selection of one unit from a set of N (the population) made in such a way (theoretically at least) that each of of the N units is equally likely to be the unit selected.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

What is random selection different than?

A

Biased Selection

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

What type of selection process does not give each of the N units an equal chance to be selected?

A

Biased Selection

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

Is randomness valid or is it a theoretical construct of questionable validity?

A

This is difficult to say. Most random number generators on computers are based off of algorithms on the computer clock. It has been shown that if you learn the first number in a sequence you can reliably predict the following numbers based on prescient knowledge of the algorithm.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

What is set theory?

A

It is the branch of mathematical logic that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics. The language of set theory can be used in the definitions of nearly all mathematical objects.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q

What is a group of distinct objects of any well defined nature?

A

A set.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

Are sets finite (people in the room) or infinite (all integers)

A

They can be either or.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
17
Q

Elements are?

A

Members of the set

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
18
Q

What is a simple experiment (in set theory)?

A

A process for generating a set

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
19
Q

Define a sample space

A

Set of all possible distinct outcomes for a simple experiment.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
20
Q

How does one notate a sample space?

A

“(S)”

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
21
Q

What is an elementary event?

A

A single member of the sample space

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
22
Q

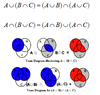
What does this formula state?

A

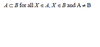
A is a subset of B where X is a member of X and X is a member of B but A does not equal B.

This called a proper subset.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
23
Q

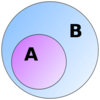
What does this (See below) refer to?

{}

A

An empty set or a null set.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
24
Q

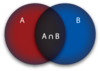
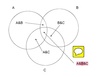
What is the complement?

A

a complement of a set A refers to things not in (that is, things outside of), A.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
25
Q

How is the compliment of A written?

A

A~

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
26
Q

What does cardinality mean in set theory?

A

For a given set A

|A| = the number of elements of A

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
27
Q

What are the set operations?

A
  1. Intersection
  2. Union
  3. Difference
28
Q

Describe Intersection (AND)?

A

A intersects B is equal to X such that X is a member of A and X is a member of B

29
Q

Describe Union (OR)

A

A union B equals A set of elements such that X is a member of A OR X is a member of B

30
Q

Describe the difference

A

The difference between A and B is equal to elements X such that X is a member of A and X is not a member of B.

31
Q

How is the interesection (AND) graphically represented?

A
32
Q

How is the union (OR) graphically represented?

A
33
Q

How is the difference (-) graphically represented?

A
34
Q

What is De Morgan’s law?

A

The complement of the intersection of A and B is equal to the complement of A union of the complement of B.

(A&B)~ equals A~OR B~

ALSO

The complement of the union of A B is equal to the complent of A intersected with compement of B

(AORB)~ = A~&B~

35
Q

How else can De Morgan’s laws be noted?

A
36
Q

Are there distributive laws for sets?

What does this mean?

A

Yes. That sets undergo distributive operations similar to ones done in algebra for numerical operations.

37
Q

Give me an example of distributive aspects of sets

A
38
Q

What is described as the occurance of an event in one set exludes the occurance of an event in another set?

A

Mutually exlusive sets

39
Q

What is the interesection of a mutually exclusive set?

A

The empty set, {}

40
Q

What is described as each member of S must exist as at least one set.

A

Exhausitive sets (all elements are accounted for)

Another way to describe collectively exhaustive events, is that their union must cover all the events within the entire sample space. For example, events A and B are said to be collectively exhaustive if

41
Q

What is partition?

(Not the Beyonce song)

A

When sets are both mutally exclusive and exhausitve.

42
Q

What is the range of probability for any given event?

A

0<=P(A)<=1

43
Q

What is the probability of at least on of all events occuring (S)?

A

P(S)=1

44
Q

What is the probability of the empty set {}?

A

P({})=0

45
Q

What is the probability of the completement of all events occuring (~S)?

A

0

46
Q

P(S) + P(~S) =

A

1

47
Q

P(~A) =

Why?

A

1 - P(A)

48
Q

Are probabilities proportions?

What does this mean?

A

HELL YES.

That laws of probabilities are the the same as the laws of proportions.

49
Q

What are the two types of probability laws?

A
  1. General
    • basic laws governing proportions (probabilities) across wide settings
  2. Specific
    • specific ocnditions on sampling, independence, number of categories etc
50
Q

What is the probability for P(A or B)?

Given that the sets (A,B) are mutually exclusive

and NOT mutually exclusive

A

Mutually exclusive:

P(A) + P(B)

NOT Mutually exclusive:

P(A) + P(B) - P(A&B)

51
Q

What type of OR do we use in probability laws?

A

Classical OR which means either or both.

NOT either (one or the other).

52
Q

How do we genralize a formula across three events?

A

P(A or B or C) = P(A) + P(B) + P(C)
- P(A&B) – P(A&C) – P(B&C)
+ P(A&B&C)

53
Q

What is a conditional probability?

A

A conditional probability measures the probability of an event given that (by assumption, presumption, assertion or evidence) another event has occurred.[1] If the events are A and B respectively, this is said to be “the probability of A given B”. It is commonly denoted by P(A|B)

Another definition: conditional probability of A given B is the
proportion of units having characteristic A
among only those units that also have
characteristic B

54
Q

What is the formula for a conditional probability?

A
55
Q

What must be true for a conditional probability to be true?

A

(B) does not equal 0

P(B) and P(A) must be part of the same sample space (S)

56
Q

What does this mean P(A|S)?

Can it be simplified?

If so to what?

A

Probability of A given S where S is the universe of all possible events.

Yes it can be simplified.

P(A|S) = P(A)

**this is only when the refrence set is the universal set (S).

57
Q

How is the probability of joint events expressed?

A
58
Q

What is implied via this formula?

A

That the events are dependent.

59
Q

How would one express events that occur together that are independent?

A
60
Q

What is statistical independence?

A

When the two characteristics of A nd B are independent of the proportion of units having one characteristic is the same irrespective of whether the refrence group is the entire population or is simply the subpopulation of unist having the other characteristic.

e.g. P(A|S) = 0.5

P(A|B) = 0.5

P(B|S) = 0.7

P(B|A) = 0.7

61
Q

What does it mean if the characteristics are dependent (i.e. not independent)?

A

Alternatively, characteristics A and B are
independent if the probability than an incident
will have one characteristic, conditional upon its
having the other, is the same as the
unconditional probability that it will have the first
characteristic.

e.g.

P(A|S)= 0.5

P(B|S) = 0.7

P(A|B) = 0.54

P(A&B) = 0.54*0.7 = 0.378

62
Q

Uh oh…Derive Bayes Theorem (write it out)

A
63
Q

What is a generalization of Bayes Theorem?

A

Suppose that A is actually A1, A2, A3 etc.

P(A) = P(A1) + P(A2) + P(A3)…

therfore the formula for P(A&B) = (see below)

64
Q

What are the five conditions to be met for statisical independence?

How many need to be met for independent characteristics to be concluded?

A
  1. P(A|B)=P(A)
  2. P(B|A)=P(B)
  3. P(A&B)=P(A)P(B)
  4. P(A)=0
  5. P(B)=0

JUST ONE!!!!!

65
Q

Describe the Bayes Theorem as it pertainst to updates on probability.

A

The prior probability P(A) is upated by new information P(B) which creates a posterior probability of P(A|B)

66
Q

Contingency table for two mutually exclusive
and exhaustive events A & B

A

Stats Test 1 - "It's all intuitive." (4 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2024 Bold Learning Solutions. Terms and Conditions