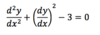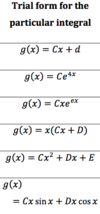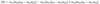General Math Deck

Question 1

What are the three ways of multiplying vectors, and what are their respective outcomes?

Answer 1

• Multiplying a vector by a scalar (also known as scaling)
• Multiplying two vectors to obtain a scalar (dot product)
• Multiplying two vectors to obtain a new vector (vector product)

Question 2

What is the expression for the dot product?

Answer 2

It is defined as being the product of the magnitude of the two vectors multiplied by the cosine of the angle 𝜃 between them.

Question 3

What is the vector product/cross product?

Answer 3

The magnitude of the vector product of two vectors is defined as the product of their magntitudes multiplied by the sine of the angle 𝜃.

The vector product is a vector that acts perpendicular to both vectors A and B.

If you curl your fingers in your right hand in the direction of the first vector A to the second vector B, then the direction of the cross product is given by the thumb.

Question 4

Before you add matrices, what do both matrices need to have?

Answer 4

They need to have the same dimensions.

Question 5

What conformability to do need for both the matrices before multiplying?

If there is conformability what are the dimensions of the product matrix?

Answer 5

The column of the ‘lead’ (1st) matrix must be equal to the row of the ‘lag’ (2nd) matrix.

It is equal to the rows of the ‘lead’ matrix and the columns of the ‘lag’ matrix.

Question 6

If two matrices conform for multiplication, what would be the values be in the product?

Answer 6

Individual values would be equal to sum of the product of the individual values in the row(lead matrix) and columns (lag matrix).

Question 7

Matrix multiplication commutative and associative?

Answer 7

Not commutative, but is associative and distributive.

Question 8

Determinants are only defined for…

Answer 8

square matrices.

Question 9

How is the determinant of a 2x2 matrix determined?

Answer 9

Question 10

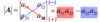
How would you determine the determinant of the this 3x3 matrix?

Using the most intuitive method.

Answer 10

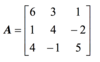
First add the first two columns of the matrix as two new columns 4 and 5 on the right.

All the terms you add are determined by creating diagonals going to the right. Starting from a₁₁ and going to a₁₃ .

All the terms you subtract are determined by going from the left, a₁₂, to a₁₃ .

Question 11

What is the cofactor and how is it defined?

Answer 11

M_ij is the minor of the row and column defined.

the -1 raised to the power of the row and column, is the same sign as the minor if the sum of i and j is even. It is the opposite sign if the sum is odd.

Question 12

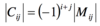
How can the third order determinant be expressed through the laplace expansion ?

Answer 12

Plug in the values for a₁₁ to a₁₃

Determine the cofactors for each of the minors.

Question 13

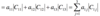
What does interchanging any two rows (or columns) do to the value of the determinant?

Answer 13

It will change the sign but not the magnitude.

Question 14

What does multiplying any row (or column) by a scalar do to the determinant?

Answer 14

It will change the determinant by k-fold.

Question 15

If one row (or column) is a multiple of another row (or column), what is the value of the determinant?

Answer 15

zero

Question 16

Under what conditions can an inverse matrix be defined for a matrix?

Answer 16

It can be defined if it is a square matrix.

Question 17

What does a matrix require to be non-singular?

Answer 17

its rows (or columns) must be linearly independent.

Question 18

What is the rank of a matrix?

Answer 18

The rank is defined as the maximum number of linearly independent rows or columns in the matrix.

A n*n non-singular matrix is of rank n.

For a m*n the rank can be at most n or m, whichever is smaller.

Another way of determining the rank would be to find out the maximum number of non-vanishing determinants that can be constructed from the rows and the columns of the matrix.

Question 19

Can you determine the cofactor for each element in a matrix?

Answer 19

Yes.

Question 20

Whats really important that you need remember when multiplying matrices?

Answer 20

You need to be multiplying across the row of one matrix and the column of another.

One row maintains fixed as you move across the columns of the other matrix.

Keep focused! Its easy to mess it up!

Question 21

What is the general formula for the inverse of a matrix?

Answer 21

Where the determinant is for the original matrix.

The cofactor of a matrix needs to be transposed to obtain the adjoint.

Question 22

How do you find the cartesian eq from a vector equation?

Answer 22

Separate all the vector components into their respective cartesian formats.

From the resultant eq, try to combine to obtain one cartesian eq.

Question 23

What is the scalar product form?

Answer 23

Question 24

Explain why this is the case.

Answer 24

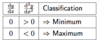
1. When the 1st derivate is 0 but the 2nd derivative is positive, it implies that the slope of the gradient is positive, so it is increasing as we move across from left to right. If the gradient is going from negative to positive as we move from left to right, we know that the critical point is a minimum.
2. If the 2nd derivative is negative, it implies that the gradient is becoming more negative as we move across from left to right. A gradient decreasing in value happens with maximums.

Question 25

What is the integral of this expression?

Answer 25

Question 26

What is d(y²)/dx?

Answer 26

Using the chain rule the outcome would be: 2y(dy/dx)

Question 27

Integration by parts formula.

Answer 27

Remember the value you get by integrating is in both terms.

Question 28

What is the order of a ODE?

Answer 28

It is the order of the highest derivative in the equation.

Question 29

What defines an ODE as linear or non-linear?

Is the attached expression linear or non-linear?

Answer 29

A differential equation is linear if the terms involving the dependent variable (y in dy/dx) and its derivatives are all linear terms.

An ODE is linear if the unknown function (e.g. y) and its derivatives appear to power one. Also if there is no product of the unkown function and its derivatives.

Its non-linear because of sin(y) as well as y(dy/dx)

Question 30

Linear or non-linear?

Answer 30

non-linear because of the absolute term

Question 31

What is the degree of an ODE?

What is the degree of the attached derivative?

Answer 31

The degree is the highest power the highest derivative is raised to.

First degree, the degree is determined by the highest derivative.

Question 32

What makes an ODE homogenous or non-homogenous?

Answer 32

The homogeneity is determined by putting all the terms containing the dependent variable on the LHS and all the rest of the variables on the right-hand side.

If the terms on the RHS equate to zero, the ODE is said to be homogenous. If it isn’t equal to zero, then it’s non-homogenous.

Question 33

Homogenous or non-homogeneous?

Answer 33

Homogenous, because all the x values are attached to the dependent y, so they stay on the LHS.

Question 34

Does the differential equation have to be linear to apply the integration factor method?

Answer 34

Yes it does.

Question 35

If you’re going to use the integration factor method, can the derivative term have any coefficients?

Answer 35

No it can’t, any coefficients need to be divided out.

Question 36

How do you obtain the general solution of a 2nd order homogenous ODE?

For real distinct roots.

Answer 36

The general solution is of the form 𝑦 = 𝐴𝑒^𝑚₁𝑥+ 𝐵𝑒^𝑚₂𝑥 .

The value of m can be found through the auxiliary equation, 𝒂𝒎^𝟐 + 𝒃𝒎 + 𝒄 = 𝟎

The values of a, b, c are the coefficients of the respective terms in the ODE.

The values m1 and m2 are plugged back into the general solution equation.

To find the constants A and B, initial conditions are required.

Question 37

How do you obtain the general solution of a 2nd order homogeneous ODE with real coincident roots?

Answer 37

Similar to real distinct roots, however, the auxiliary equation required is slightly different.

𝑦 = 𝐴𝑒^𝑚𝑥 + 𝐵𝑥𝑒^𝑚𝑥

Compared to the auxiliary equation for real distinct roots, one of the 𝑒^𝑚𝑥 terms has an x in it. This is the only difference.

Question 38

What is the auxiliary equation for a 2nd order homogeneous ODE with complex roots?

Answer 38

𝒚 = 𝒆^𝒑𝒙( 𝑪*𝐜𝐨𝐬(𝒒𝒙) + 𝑫*𝐬𝐢𝐧(𝒒𝒙) )

Question 39

How do you solve non-homogeneous 2nd order ODEs?

Answer 39

The general solution for a non-homogeneous 2nd order ODE is the sum of the complementary function and the particular integral.

The complementary function is based on the auxiliary equations required for homogeneous 2nd order ODEs. To solve it the RHS of the ODE is equal to zero.

To find the particular integral, you first need to know the form. This can be given, or it has to be found. Once the form is obtained, find the first and second derivatives of the form and plug back into the equation.

To solve, equate the ‘x’ terms on the LHS to the RHS, and similarly, the leftover terms on the LHS equate them to the RHS.

Question 40

How do you find the form of the particular integral?

Answer 40

First, try the same form as Q(x).

If this form is the same as any of the terms in the complementary function, try x*Q(x).

If this is still doesn’t work, try x²*Q(x)

Question 41

For each of these complementary functions and forms of Q(x), what is the most suitable first choice for the particular integral?

Answer 41

Question 42

What makes a set of vectors linearly independent?

Answer 42

Set of vectors are linearly independent if no vector in the set is a scalar multiple of another vector in the set.

It is also linearly independent if the vector isn’t a linear combination of any of the other vectors (addition or subtraction).

Question 43

What is the relation between a and b?

What is the relation between a and d?

What is the relation between a, b and c?

Answer 43

a and b are linearly independent

a and d are linearly dependent

c is a linear combination of a and b, so the vectors are linearly dependent.

Question 44

What are the two types of random variables?

And what are the two probability distribution functions?

Answer 44

A random variable can either be discrete or continuous.

The distribution of a discrete random variable can be specified by a probability mass function.

The distribution of a continuous random variable is specified, by a probability density function.

Question 45

What is the expected value of a random variable X? And what does it represent?

Answer 45

The expected value (denoted by E(X) ) of a random variable X is a ‘weighted average’ of X with respect to its underlying probability distribution.

Question 46

How would you find the expectation value of a discrete random variable X?

Answer 46

Question 47

How would you find the expectation value of a continuous random variable X?

Answer 47

Question 48

What is the rank of a n*n non-singular matrix?

Answer 48

A n*n non-singular matrix is of rank n.

Question 49

How do you determine the stationary points of a multivariate function?

Answer 49

[x refers to first coordinate and y refers to 2 nd coordinate, (x₀ ,y ₀)]

First, find the partial derivates.

By equating the partial derivates to zero the stationary points can be found.

To determine the nature of these stationary points, the discriminant needs to be determined.

The discriminant consists of the product of both 2nd order partial derivates minus the 2nd order differential of y partial derivate wrt x.

If ∆ > 0 and the 2nd partial derivative of the first coordinate f_xx < 0 then it’s a maximum.

If ∆ > 0 and the 2nd partial derivative of the first coordinate f_xx > 0 then it’s a minimum.

If ∆< 0, it’s a saddle point: thus it is neither maximum or minimum.

If ∆= 0, it’s not possible to classify stationary points using this method.

Question 50

How would you determine the stationary points of partial derivative equations coming from a multivariate equation?

Answer 50

For each partial derivative, you need to determine the values of BOTH variables that would result in 0.

Question 51

What z score range do you use to get the 95% confidence interval for normal distribution?

Answer 51

Question 52

If you need to divide the LHS by a matrix on the RHS, what do you do?

Answer 52

You can’t actually divide by you can multiply by the matrix inverted.

The inverted matrix is equal to the C^T (cofactor transposed), and then divided by the modulus of the determinant.

Remember how to take the determinant of 3x3.

Question 53

What is the matrix of cofactors for a 3x3?

Answer 53

Question 54

What does the determinant of a 3x3 matrix look like?

What do you need to remember?

Answer 54

You across the top values.

The determinants are obtained by drawing a line through the row and column the top value is in, then the determinant is applied on the remaining 2x2 set of values.

A key thing to remember is that the middle term is negative, in the same way, it is in the cross product.

Question 55

For a normal distribution, what do these values represent?

Answer 55

The mean and the standard deviation.