general

Question 1

Bayesian vs frequentist probability

Answer 1

Bayesian - degree of belief

Frequentist - proportion p of the repetition results in the given outcome with probability p

Question 2

Random variable

Answer 2

Description of states which are possible, coupled with a probability distribution. Can be discrete or continuous.

Question 3

Probability mass function P(x)

Answer 3

Maps from a state of a random variable to the probability of that rv taking on that state. Tied to the random variable P(x) != P(y) Sum over all x of P(x) = 1 - normalized

Question 4

Joint probability distribution

Answer 4

PMF that acts on many random variables at the same time.

Question 5

Expected value

Answer 5

Of some function f(x) with respect to a probability distribution P(x) is the average, or mean value, that f takes on when x is drawn from P.

Question 6

Variance

Answer 6

gives a measure of how much the values of a function of a random

variable x vary as we sample different values of x from its probability distribution:

Question 7

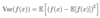
Low variance implies

Answer 7

The values of f(x) cluster near their expected value. The square root of the variance is known as the Standard deviation.

Question 8

Covariance

Answer 8

Gives some sense of how much two values are linearly related to each other, as well as the scale of the variables:

Question 9

principle of optimality

Answer 9

Has an optimal substructure.

An MDP problem that can be broken into smaller parts and solved optimally.

Can be broken down into doing the best thing for the next step and the best thing from there onwards.

Question 10

Bellman expectation equation

Answer 10

One step lookahead

It writes the value of a decision problem at a certain point in time in terms of the payoff from some initial choices and the value of the remaining decision problem that results from those initial choices.

Question 11

acting greedy (policy)

Answer 11

maximizing short therm reward/.

max of action-value function.

Question 12

methods to solve an MDP

Answer 12

policy iteration and value iteration

VI: look at all states and update the value function at every state, using the previous iteration. Build a new value func at each state.

Question 13

Value function

Answer 13

Expected return for a state

Question 14

How to calculate Incremental Mean

Answer 14

Question 15

On-policy vs off-policy learning

Answer 15

On-policy learning

• “Learn on the job”
• Learn about policy π from experience sampled from π

Off-policy learning

• “Look over someone’s shoulder”
• Learn about policy π from experience sampled from µ

Question 16

2 steps of Monte-Carlo Control

Answer 16

Every episode:

1) Policy evaluation Monte-Carlo policy evaluation, Q ≈ qπ
2) Policy improvement -greedy policy improvement

Question 17

Greedy in the Limit with Infinite Exploration (GLIE)

Answer 17

Question 18

GLIE Monte-Carlo Control theorem

Answer 18

Theorem GLIE Monte-Carlo control converges to the optimal action-value function, Q(s, a) → q∗(s, a)

Question 19

SARSA update

Updating Actio-Value functions (Q) with SARSA

Answer 19

Question 20

SARSA algorithm for on-policy control

Answer 20

Question 22

Bootstrapping - bias vs variance trade-off

Answer 22

bootstrapping increases the bias

Question 23

Q-Learning vs Sarsa

Answer 23