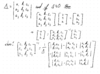General

Question 1

Fourier Transform

Answer 1

This is a way to describe an oscillating function in terms of angle and intensity by changing the function to be a function of angular frequency (rad/sec) or wavenumber (k=seconds to complete a wave).

It uses eulers identity to switch the imaginary parts of the frequency into cos and sine terms. This is then converted into polar coordinates in the intensity phase space.

Use the table to convert regular functions in fourier equations that are used to analyze a frequency.

In the manual the period is given so 2 pi over the angular frequency give syou seconds and the functions for several common signal inputs.

Question 2

Even and odd functions

Answer 2

f(-x)=f(x) means the function is even (x² cos)

f(-x)=-f(x) means that it is odd (x³ sin)

Question 3

Orthogonal functions

Answer 3

This is when the integral of f(x)*g(x)=0

Question 4

Taylor Series

Answer 4

Taylor Series represent using a series of bisected functions to model an original function f(x). They converge when |x-a|

Question 5

Fourier transform of a cosine wave

Answer 5

This will yield one line because each and every interval is on the same frequency which means your peak will show that one frequency.

Question 6

Fourier transform of a series of signals with t(duration)=tau

Answer 6

This will yield several bumps because thetime domain shows 2 intensities within one 360 degree rotation.

Question 7

Integers, rational, and irrational numbers

Answer 7

Integers are whole numbers

Rational numbers are numbers that can be written as a ratio of two integers

irrational numbers cannot be expressed as a ratio of two integers. They include numbers that repeat or do not terminate Ex: (3)^.5/2

This is irrational because 3^.5 has an operator

Real numbers: include all of the above

Question 8

factorial

Answer 8

n!=(n)*(n-1)*…(2)*(1)

Question 9

Complex Numbers (Add, Subtract, multiply, divide)

Answer 9

Add/subtract: combine like terms.

Mult.: FOIL

Divide: Multiply by the conjugate of the denominator

Question 10

Using conjugates

Answer 10

if A=a+ib and A#=a-ib then A*A#=a² + b²

Question 11

Sets

Answer 11

A set is a collection of objects or entities. If X belongs to a set S then X ∈ S where S={n₀,n₁…n} or a set could be defined by a function S={X:X³>27 }

Question 12

Joining Sets

Answer 12

∈

C ∪ D = {X:X∈C or X∈D) This is the union of sets C and D

C ∩ D = {X:X∈C and X∈D) This is the intersection of sets C and D

And if all of a set (set A) are part of a larger set (set B) then AcB where the c is the inclusion symbol

Question 13

Ø

Answer 13

This is the null set symbol. It means that there are not any elements within a set.

Question 14

Exponent Laws

Answer 14

ⁿ√a=a^(1/n)

a^m/aⁿ= a^m-n a^m*aⁿ= a^m+n

(a^m)ⁿ=a^m*n

(a*b)^m= a^m*b^m

Question 15

Simplify ⁿ √a^m

Answer 15

ⁿ √a^m= a^(1/n)*m = a ^(m/n)

Question 16

Simplify ⁿ √ab

Answer 16

ⁿ √ab= a^(1/n) * b^(1/n)

Question 17

How to take the root of a function with a divisor

Answer 17

Multiply the denominator through and divide the whole term by the diviseor with the root operator used.

Question 18

Rule for binomial expansion

Answer 18

if we have a binomial given by (A+X)ⁿ then the expansion is given by B*A^n-m * X^m

Where: m=term # starting from 0 to n+1

B=(The exponent*coefficient of the term m-1)/m

Ex: Term 3 of (A+X)⁷ is given by A⁷+7A⁶X+(7*6/2)A⁵X²…

Question 19

Determinants

Answer 19

Determinants are the values of matrices. The order of a determinant is given by the sqaure root of the number of elements which are the numbers inside of the matrix.

Question 20

determinant nomenclature

Answer 20

the position of any value is given by a_ij where i= row # and j = collumn #

Question 21

Finding determinants of second order matrix

Answer 21

If the determinant is second order then the determinant is given by:

Product of primary diagonal-Product of secondary diagonal

Where: Primary diagonal are the values given by a₁₁ and a₂₂ and the secondary diagonal is given by the values a₂₁ and a₁₂

Question 22

Minor of a matrix

Answer 22

This is the reduced matrix that can be used to find the determinant of higher order matrices. The order is given by crossing out the values that intersect at the value of interest and finding the determinant of the resulting matrix multiplied by the value of interest.

Question 23

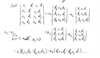
Sign of determinant parts

Answer 23

If the leading coefficient is in the position ij where i+j is

even then the coefficient is positive

odd then the coefficient is negative

Question 24

Solving Linear Equations with two unknowns

Answer 24

when given a set of equations like

a₁x+b₁y=c₁ and a₂x+b₂y=c₂

Multiply the the first equation by -a₂ and the second by a₁ so that when added the first terms cancel. This enables you to have only one unknown to be solved for.

y=(-a₂c₁+a₂c₂)/(a₁b₂-a₂b₁) and x=(c₁b₂-c₂b₁)/(a₁b₂-a₂b₁)

Question 25

Solving linear equations with 3 unknowns

Answer 25

If we have three equations we can create three matrices; C=A*b where A=3x3 coefficient matrix, b = 3x1 matrix of xyz (or any three unknowns) and C= 3x1 matrix of constants

Then b= A^-1*C

Question 26

Scalar Product

Answer 26

a dot b= a_x*b_x+a_y*b_y+a_z*b_z=|a|*|b|*cos(alpha)

Where: a dot b represents the magnitude of the shared a and b vector space

Question 27

Cross Product

Answer 27

axb is the cross product of a and b and represents the magnitude of the distance between the tips of a nd b in the direction that is normal to the plane created by a and b.

axb is given by the determinate of a and b

axb=

|a_x a_y a_z|

|b_x b_y b_z|

i j k |

Question 28

How to solve third order algebraic equations when one root is given

Answer 28

When one root is given you can divide the third order equation by the root to make it a quadratic which is then solved via the quadratic formula.

Question 29

Long division for equations

Answer 29

To do long division of an equation you always eliminate the higher order term.

Question 30

Basic logarithm function

Answer 30

The answer to a log is the exponent

log_bn=a -> b^a=n and n=b^{logb^n}

Question 31

log_b1=?

Answer 31

=0 because b⁰=1

Question 32

log_bb=?

Answer 32

=1 because b¹=b

Question 33

expand: log_bm*n

Answer 33

log_bm*n= log_bm+log_bn

Question 34

expand: lob_b(m/n)

Answer 34

log_b(m/n)=log_bm-log_bn

Question 35

log_b(1/n)=?

Answer 35

log_b(1/n)=-log_bn because log_bn^-1=-1*log_bn

Question 36

log_bm^(1/n)=?

Answer 36

log_bm^(1/n)=(1/n)*log_bm

Question 37

radians to degrees formula

Answer 37

radians= degrees * (pi/180) AKA there are 180^o in pi radians

Question 38

30^o to radians

Answer 38

30^o=pi/6 radians

Question 39

pi/3 radians to degrees

Answer 39

60^o

Question 40

45^o to radians

Answer 40

pi/4

Question 41

275^o to radians

Answer 41

5pi/4 radians

Question 42

3pi/2 to degrees

Answer 42

270^o

Question 43

330^o to radians

Answer 43

-pi/6 or 11pi/6

Question 44

5pi/3 to degrees

Answer 44

300^o

Question 45

120^o to radians

Answer 45

2pi/3 radians

Question 46

rpm to rad/sec

Answer 46

rpm*(360/rev)*(pi rad/180)*(min/60 sec)=rad/sec

Question 47

sin, cos, tan of 17pi/6

Answer 47

17pi/6= 12pi/6+5pi/6

sin(5pi/6)=1/2

cos(5pi/6)= -3^.5/2

tan(5pi/6)= -1/3^.5

Question 48

sin, cos, tan 5pi/3

Answer 48

sin (5pi/3)= -3^.5/2

cos(5pi/3)= 1/2

tan(5pi/3) = -3^.5

Question 49

polar coordinate transform

Answer 49

(x, y) = (r, θ)

where: r=(x² + y²) and θ=tan^-1(y/x)

x=rcosθ and y = rsinθ

Question 50

Law of cosines

Answer 50

for a triangle with angles A,B,C opposite to sides a,b,c

c² = a² + b² - 2abcos(C)

Question 51

Law of sines

Answer 51

a/sin(A)=b/sin(B)=c/sin(C)

Question 52

Using law of cosines

Answer 52

Law of cosines can be used to find:

Distances between objects starting at one point and travelling in different directions.

diagonals of a parallelagram

Question 53

General Equation for a line

Answer 53

Ax+By+C=0

m=-A/B and

b=-C/B

Question 54

slope intercept line equation

Answer 54

y=mx+b where:

m=(y2-y1)/(x2-x1)

Question 55

two point line formula

Answer 55

y-y1/x-x1=(y2-y1)/(x2-x1)

Question 56

Slope relationship between perpendicular lines

Answer 56

m₁=-1/m₂

Question 57

angle between two lines where m₁>m₂

Answer 57

tan(α)=(m₁-m₂)/(1+m₁*m₂)

Question 58

general equation for conic sections

Answer 58

ANY second order equation

Ax² + Bxy + Cy² + Dx + Ey + F

Question 59

criterion for ellipse, parabola, and hyperbola

Answer 59

ellipses occur when (B²-4AC)<0

parabolas occur when (B²-4AC)=0

Hyperbolas occur when (B²-4AC)>0

Question 60

ellipse equation

Answer 60

(x-h)²/a² + (y-k)²/b² = 1

where C=(h,k) and a,b are the radius in the x and y directions

Question 61

Limits

Answer 61

Limits are the value a function approaches at some independent variable value.

If, the function exists at the limit then it is continuous.

Question 62

L’Hospital’s Rule

Answer 62

Suppose we have two functions, f(x) and F(x) where both go to zero as x approaches A. The limit for f(x)/F(x) is given by f’(x)/F ‘ (x)

Question 63

Formal definition of a derivative

Answer 63

The derivative of a function, y=f(x) is the instantaneous rate of change or

dy/dx=lim (Δx->0) (Δy)/(Δx) and can be proven by subbing y+Δy for y and x+Δx for x within a function given by y=f(x) and then solving for Δy/Δx and taking the limit as Δx approaches 0

Question 64

mulitplication rule for derivatives

Answer 64

d/dx u*v= u dv/dx + v du/dx

Question 65

power rule for derivatives

Answer 65

y=n x^m

y’ = (m*n)x^m-1

Question 66

d/dx uⁿ = ? where u = f(x)

Answer 66

d/dx uⁿ = nu^n-1 du/dx via the chain rule

Question 67

d/dx (v^u) where both v and u =f(x)

Answer 67

d/dx(v^u) = u*v^u-1 dv/dx + v^u lnv du/dx

Question 68

d/dx (u/v)=?

Answer 68

d/dx (u/v) = [v(du/dx) - u(dv/dx)] / v²

Question 69

d/dx (log_cu) = ? where u=f(x) and c=constant

Answer 69

d/dx (log_cu) = 1/u log_ce * du/dx

Question 70

How to treat derivatives

Answer 70

Derivatives act as differentials so they can be inversed or have parts cancel (eg (dy/dt)/(dx/dt)=dy/dx

Question 71

Implicit differentiation

Answer 71

if f(x,y)=c then to find dy/dx

1. ) differentiate f(x,y) where d/dx(xy)= y + x(dy/dx)
2. ) isolate dy/dx

Question 72

partial derivatives

Answer 72

These are written with the funky d symbol (∂) or f ‘_x and are formally defined by

if z=f(x,y) then ∂f/∂x = lim Δx->0 [f(x+Δx,y) - f(x,y)]/ (Δx)

where: if the variable is not in the denominator it is treated like a constant

Question 73

chain rule for partial derivatives

Answer 73

if z=f(x,y) and x=f(t) ; y =f(t) then ∂z/∂t = [(∂z/∂x * ∂x/∂t) + (∂z/∂y * ∂y/∂t)]

Question 74

Meaning of f ‘ and f ‘’ being greater than zero

Answer 74

if f ‘ >0 then the slope of f at whatever x is positive so f(x+dx)>f(x)

if f ‘’ >0 then the slope of f at x is increasing therefore f ‘ (x+ dx)> f ‘ (x)

Question 75

Procedure for finding maxima/minima

Answer 75

1. ) find the first derivative
2. ) Find the values of x so that the first derivative (f ‘ )=0 . These are the function’s critcal values
3. ) find the second derivative f ‘’
4. ) Substitute the critical values from 2 into f ‘’

if f ‘’ (x)>0 then at x there is a local minima

if f ‘’ (x) <0 then at x there is a local maxima

Question 76

Solving for local maxima/minima when f’‘=0

Answer 76

To evaluate if f(x) is a local maxima or minima when f ‘’ is 0 you must find f ‘ (x+1) and f ‘ (x-1) and use those values to evaluate what f(x) is

Question 77

Integration

Answer 77

This is the process of finding the function where the function’s derivative is given

d( ∫ f(x) dx) = f(x) dx

∫=the function whose differential is

Question 78

anti-derivative: Power rule

Answer 78

∫ ax^b dx = [ax^b+1/(b+1)] + c

Question 79

definite integral definition

Answer 79

∫_a^b f(x) dx = F(b)-F(a)

Question 80

Integration by Parts

Answer 80

When the integrand can be split into two functions; one that represents a u where u=f(x) and another that represents dv where dv=g(x)dx and g(x) is easily integrated.

Under these conditions: ∫ udv = uv - ∫ vdu

Question 81

Common functions for integration by parts

Answer 81

Generally allow ln to be u (du=dx/x) and x, e^x, or other easily integrated functions be dv

Question 82

How to use dy in a double integral

Answer 82

When using dy the slice is taken perpendicular to the y axis.

1. ) with f(x) solve for x so that way x=f(y)
2. ) determine the bounds and integrate ∫ f(y) dy

Question 83

Formula for generating a solid around the x axis

Answer 83

V= ∫_a^b pi y² dx

where y= f(x)

Question 84

Laplace Transformation

Answer 84

These involve the transformation of derivatives where ∫₀^inf e ^-st F(t) dt = f(s) and can be written f(s) = L {F(t)} = L{F} = F(s)

Question 85

∫ e ^{x n} =?

Answer 85

∫ e ^{x n} dn = (1/x) e ^{x n} + c

Question 86

Finding F_r for coplanar and parallel forces

Answer 86

F_r= ΣF

d_r = ΣF_i*d_i / ΣF_i where d is the perpendicular distance to some point O

Question 87

F_r for concurrent force systems?

Answer 87

F_r = Σ F_i where each F is a vector so vector addition is used. This is a system where all the forces intersect at one point.

Question 88

Non Concurrent force systems: F_r and d_r = ?

Answer 88

In a nonconcurrent system the forces do not intersect at a common point and the body is not static. A moment around the center of gravity is given by

Σ F_i * d_i = F_r * d_r

where the direction of F_r is determined by vector addition

Question 89

Couple

Answer 89

A couple is a torque that is produced by two parallel but opposite forces. The resulting moment is given by M= F*d where d is the total distance between the parallel forces and F is the force of one of the forces

The magnitude of the couple is not a function of location. AKA the couple has the same magnitude regardless the center of the moment.

Question 90

Solving static structures: Method of Joints

Answer 90

The idea of this method is that each joint must be in equilibrium therefore if we isolate each and every joint and solve for the internal forces then each will be in equilibrium. Procedure:

1. ) Draw FBD with everything internal in tension
2. ) Solve for the reaction forces (use logic not tension)
3. ) choose a joint where 2 unknowns exist and solve.
4. ) rinse and repeat

Question 91

Equations of Equilibrium

Answer 91

This says that for a static body:

ΣF_x = ΣF_y = ΣF_z = ΣM₀ = 0

When solving a structure we can assume that the internal reactions cancel each other out and only treat the system by analyzing the external forces with these equations.

Question 92

Method of Sections

Answer 92

This “cuts” the structure and analyzes the internal forces at the cut. Procedure:

1. ) Draw FBD
2. ) solve for Rxns
3. ) “cut” the structure and draw internal forces in tension. Do NOT cut more than three members at once.
4. ) ΣMo = 0 where o is the intersection of two of the forces which leaves the third unknown and the external forces which makes solving easy.
5. ) ΣFx = ΣFy =0 solve for the other two unknowns

Question 93

What is the tension in a cable/rope equal to?

Answer 93

Tension in a cable or a rope is constant throughout the cable/rope. The direction does NOT matter.

Question 94

Finding moments in 3-space

Answer 94

1. ) break forces into their three components
2. ) ΣMx = F_z*d_z + F_y * d_y It is the same as 2-space but everything that is not in the direction of the axis is considered to be causing a moment about the said axis.

Question 95

Friction

Answer 95

Friction is the contact resistance between bodies in contact with one another and is proportional to the normal force. It acts parallel to the interface across the surface and is summated at the point where the normal force acts.

F_max= N * μ_s

F_motion=N * μ_k where μ_s >μ_k

Question 96

Total force of two interacting solids

Answer 96

R = N + F_f where F_f = μ * N and the angle of R is given by tan ϕ = F_f /N= μ and ϕ is the angle between F_f and N not to the horizontal

Question 97

Belt Friction

Answer 97

This is the idea that a belt going over a solid has unequal tensions where the greater tension is in the direction of impending motion.

T_2max = T₁ *e^(μ_s*β) where β is the angle of contact in radians

Question 98

Centroids solving for CG

Answer 98

x̄ = [Σ W*x]/W and similar with the y bar

Where: x represents the distance of a homogenous chunk of the object from any defined x axis and W is the weight of that chunk.

Question 99

Centroid of areas

Answer 99

x̄ = ∫ x dA/∫dA

Question 100

centroid of lines

Answer 100

This is fundamentally similar to the centroid of an area but uses a line integral given by x̄ = ∫ x dL/∫dL where L refers to the line coordinates

This is most common for arcs where dL=rdθ and x=rcosθ and y=rsinθ

Question 101

Theorem of Pappus

Answer 101

This says that when you rotate a line about an axis 360^o that the resulting surface area is given by A=L 2 pi X where X is equal to the cg or centroid

Question 102

Theorem of Guldinus

Answer 102

This states that the volume of an area revolved around an axis is given by V = 2*pi*x*D where x is the centroid or cg of the area

Question 103

Strain and Elongation

Answer 103

When a material is put into a stress state it experiences deformation by a total amount given by δ . and the strain is given by δ/L = ε

Twisting or angular deformation is given by γ = δ/L = tan ϕ where ϕ is the angle from vertical to the deformation

Question 104

Modulus of elasticity

Answer 104

E= σ/ε = (P/A)/(δ/L) and represents the per unit stress over per unit strain within the elastic region of deformation

Question 105

Poissons ratio

Answer 105

This the ratio of lateral to longitudinal strain

Question 106

Coefficient of thermal expansion

Answer 106

δ_T = L α (ΔT)

Question 107

Solving statically indeterminate structures

Answer 107

These are structures where the number of unknowns exceeds the number of equations of equilibrium so we need to use the material properties of the material to solve.

1. ) Draw FBD for a selected member
2. ) ID known and unknowns. Write all equations to constrain via equilibrium then for material properties
3. ) Use material properties to solve for an unknown. Plug into Equations of Equlibrium.

Question 108

Twisting

Answer 108

When a shaft is placed under some torque T it experiences a shear stress τ where dF= τ dA and the internal resisting moment is given by τ r dA = dM_T

Question 109

finding shear from a torque

Answer 109

J= ∫ r² dA = the polar moment of inertia across the cross sectional area

J_max= pi*d⁴/32

and τ = Tr/J

Question 110

angle of twist

Answer 110

This is the angle of rotation caused by a torque.

It is related to the shear force by the shear modulus G.

τ / γ =G where γ is the shear strain

G= TL/θJ where J is from 0 to R

Question 111

Shear strain from twisting

Answer 111

γ = C θ /L where θ is in radians

Question 112

The angle of twist for compound shafts

Answer 112

This is the summation of individual twists. J does not depend on the material but G is material dependent

Question 113

Beam analysis

Answer 113

“walk the beam” These are usually subject to several loads and moments.

1. ) solve reactions
2. ) “walk the beam” to find moment and stress diagrams

Question 114

Sign convention for beam analysis

Answer 114

Shear is positive when walking the beam left to right and the shear points upwards.

Moments are positive when the forces on either side of the point make the beam bend like a smiley face.

Question 115

Shear diagrams at x=0 and x=L

Answer 115

The shear is ALWAYS 0 at x=0 and x=L because otherwise the beam would be mobile and not static

Question 116

Relating moments to shear

Answer 116

∫_A^B dM = ∫_A^B V dl where V=V(l) and is determined by the shear diagram

This means that the change in the bending moment from A to B = the area under the shear curve from A to B

Question 117

Flexure Formula

Answer 117

This is the formula for understanding the tension/compression within a bent beam. It says that in a uniform beam that σ_y/y = constant and that the total moment M_t = σ_max/y_max ∫ y² DA = I_y σ_max/y_max

Question 118

Position of the neutral axis

Answer 118

This influence the moment about the x axis and represents the line of the beam where σ=0 It is given by the centroid of the cross section.

Question 119

second moment of area formula

Answer 119

I_x = ∫_-l/2^l/2 y² dA where the bounds are measured from the centroid

Question 120

Parallel Axis Theorem

Answer 120

This says that the moment of inertia about any axis parallel to the neutral axis is equal to I_b = I_NA + A*D² where D is the distance from the NA to the reference axis

Question 121

General procedure for moment of inertia of composites

Answer 121

1. ) Divide each cross-section into several chunks with known Icg
2. ) located the neutral axis via finding the centroid (C = ∫ y dA/∫dA)
3. ) Calculate I_NA about each centroid.
4. ) Use the parallel axis theorem to relate each component to the overall cross-sectional I where holes are treated as negative values and the others summate.

Question 122

What are the units of moment of inertia?

Answer 122

L⁴ when solving for anything with moment of inertia try to use inches and centimeters

Question 123

Units of moments and torque

Answer 123

L*F

Question 124

Units of shear in shear diagrams

Answer 124

This is simply put in terms of pounds. It represents the total shear throughout the cross section

Question 125

Units of G/E

Answer 125

This is in F/L² because strain is unitless (L/L)

Question 126

Types of supports that create counter moments

Answer 126

Fixed connection to walls create opposite moments. These also will have shear at their open end.

Question 127

Dynamics

Answer 127

This is the study of motion of particles and bodies. Particles are point objects where it is assumed to be concentrated at one point. Bodies are systems of particles that form an object where the relative motion of different parts of the object must be considered.

Question 128

Newton’s Three Laws of Motion

Answer 128

1. ) A particle acted upon by a balanced force system has no acceleration. AKA an object in motion stays in motion unless acted upon by an external force
2. ) F=ma
3. ) Action and reaction forces are always equal and opposite

Question 129

Kinematic equations

Answer 129

Assuming that a is a constant

S= V_ot + at²/2

V_f = V_o + at

V_f² = V_o² + 2a*s

Question 130

How to use the kinematic equations

Answer 130

When a body is under constant acceleration and the problem is trying to describe the motion of a particle or body in terms of time and position identify the known variables (t_o, t_f, V_o, V_f, a) and the unknown variables.

Use the kinematic equations to solve.

Question 131

Relating s, V, and a

Answer 131

given s = f(t) then s ‘ = V(t) and s ‘’ = a(t)

Also s = ∫ V(t) = ∫∫ a(t)

Question 132

Change of position with derivatives

Answer 132

ds = (VdV)/f(V)

Question 133

Position as a function of force when F=f(t)

Answer 133

x = (1/m) ∫∫f(t) dt dt + C1*t + C2

Question 134

Angular Velocity

Answer 134

ω = θ/t where θ is in radians and the change in position is given by rθ

Question 135

Relating velocity and angular velocity

Answer 135

V = r * ω

Question 136

Angular acceleration

Answer 136

This is the change of angular velocity given by d² θ/dt² = α

Also α*dθ = ω*dω

Question 137

Do the kinematic equations apply to circular motion?

Answer 137

Yes. Replace V with ω; a with alpha; S with theta

Question 138

flight of a particle given its initial conditions

Answer 138

y:

Question 139

centripital and centrifugal acceleration

Answer 139

Centripital acceleration is a_n = V ω = rω² = V²/r and is directed towards the center of rotation

Centrifugal acceleration is a_t = dV/dt = rα + 2ω dr/dt and is directed in the direction tangent to the path of the object at that moment

Question 140

centripetal and centrifugal forces

Answer 140

the centripetal F; F_n = WV²/gr = W*a_n/g

The centrifugal F; F_t= (W/g)*dV/dt = (W/g) * a_t

Question 141

Ideal bank angle

Answer 141

tanθ = V²/gR + tanθ_f for sliding down the curve and -μ for sliding up

where: θ_f = friction angle = tan^-1 μ

θ = ideal bank angle where an object travelling at V through a curve with R will neither slide up or down.

Question 142

Forces of a rotation that is not about the object’s center of mass

Answer 142

ΣF_n = (W/g)*r_o* ω²

ΣF_t = (W/g)*r_o * α

ΣM_z = α I_z

where: r_o=the distance from the center of rotation to the center of mass of the object in rotation

I_z = I_o + m*r_o²

alpha= rotational acceleration

r_o ω² = a_n and r_o * α=a_t

Question 143

Radius of Gyration

Answer 143

k is a distance and it can regarded as the distance from the axis of inertia to the center of gravity for an object that is rotating around a center that is not outside of the object.

k = (I/m)^.5

Question 144

Rotational dynamic equilibrium

Answer 144

This is a state where V is constant and an object is rotating.

The first step is to draw FBD and find the resultant force on the said object.

In this state (W/g)r_o α d -I_zα = 0 where d is the distance from the CG to the point of rotation

Question 145

Fundamental work energy relationship

Answer 145

The work done on a translating object where the force is in the direction of motion is equal to the change in kinetic energy of that object. This is given by

F*S=(W/2g)(V_f²-V_i²)

Question 146

Work energy with variable force

Answer 146

Work = kS²/2 where k is the spring constant and S is the spring’s displacement.

Question 147

Spring constants in parallel

Answer 147

if springs are in parallel then k_f= Σ k_i

Question 148

Spring constants in a series

Answer 148

For springs in a series (1/k_f) = Σ(1/k_i)

Question 149

Frequency of oscillation: springs

Answer 149

ω = +-[2k/m]^.5 and f (1/s) = +-(1/2pi)[2k/m]^.5

Question 150

Period of oscillating springs

Answer 150

T = 1/f = 2pi[m/2k]^.5

Question 151

Conservative Systems

Answer 151

These are systems that lack friction or other dissipative forces. Therefore

KE + PE = K + U = c

and (d/dt)(KE+PE) = 0

Question 152

Solving translating systems

Answer 152

1. ) FBD
2. ) ID known forces, unknown forces, and what you are attempting to solve for
3. ) ΣF = ma = external forces

Question 153

Oscillations: Steps to solve via energy

Answer 153

1. ) FBD
2. ) if the system is conservative then

PE = W*h + kx²/2 = Wg(L-Lcosθ) + (k/2)(bsinθ)²

KE = (1/2)mV²= (1/2) m (ωL)² where ω= dθ/dt

3. ) d/dt(PE+KE)=0 and for small θ sinθ=θ and cos=1
4. ) Simply and (1/2pi)*(coefficient of θ) = f

Question 154

Momentum

Answer 154

Momentum is p=m*V and because dV/dt=a then F=dp/dt where p is a vector

Question 155

Impulse

Answer 155

This is a force that acts on an object for a short duration of time such that F(t)dt = impulse force.

∫_t0^t F(t) = (V-V₀)m = ∫_v^v mdV

Question 156

Force vs. time curves

Answer 156

If force = F = f(t) then (Σ ∫F(t))/m = dV over the period

Question 157

Conservation of Momentum

Answer 157

IF there are no external forces acting on a system then the internal components of a system have the property where m₁ * V₁ = m₂ * V₂

It generally works when dt~0 but there is a dV

Question 158

Conservation of Momentum: applications

Answer 158

conservation of momentum should be used when there is an impulse and a change in mass/velocity that occurs over dt~0

Ex: a bullet hitting a pendulum

Question 159

How to solve a bullet hitting a pendulum

Answer 159

1. ) apply the conservation of momentum to find v
2. ) assuming it is a conservative system then KE₁ + PE₁ = KE₂ + PE₂

Question 160

Impacts

Answer 160

These are when two objects collide and it is assumed that the time over which the collision takes place ~0. Therefore conservation of momentum and impulse physics applies.

Question 161

Elastic impact

Answer 161

This assumes that there is ~0 loss of energy due to deformation and impact is over a time interval =0

Question 162

Coefficient of restitution

Answer 162

this is a constant that is used to adjust for deformation upon impact of otherwise elastic objects such that

e = (relative V before)/(relative V after) = separation V/approach V where the relative nature of the velocity is described as the absolute value of their convergence/divergence

Question 163

Coefficient of restitution when collision is non-parallel

Answer 163

When collisions are non parallel but both are spheres you can break the problem down into the x and y componenets where the y component does not change unless an external force acts upon it. Therefore the coefficient of restitution only applies to the x velocities.

Question 164

Solving V_i and V_f with e and nonparallel collisions

Answer 164

1. ) Use conservation of momentum in the x and y directions. V_y does not change.
2. ) e = abs(V₂/V₁) (summate for each object)
3. ) separate e so that one of the two terms is the unknown in the conservation of momentum.
4. ) You should now have two equations and two unknowns. Solve
5. ) Use the resulting vs initial velocities to find changes in momentum, KE, or other

Question 165

Solving plane surfaces below water

Answer 165

Use pressure prisms and remember that the F_r (fluid) does NOT go through the CG of the plane.

Question 166

Solving manometer/barometer problems

Answer 166

1. ) Choose an A and B point
2. ) move from point A to B where when moving down you add P= γh
3. ) Remeber that equal heights are of equal pressures

Question 167

Center of pressure

Answer 167

When an object is submerged the center of pressure measured from the fluid surface is given by X_c = ∫ (X² dA) / ∫(X dA)

or through using the parallel axis theorem: X_c-X_o=I_o/AX_o where X_o is the CG measured from the free surface

Question 168

Tension in a thin-walled pressure cylinder

Answer 168

There are generally two stresses acting on the walls. There is the hoop stress σ₁ and the longitudinal stress, σ₃.

Note: at the boundary of the pressure and the wall there is a pressure that acts opposite to the internal pressure. On the outer edge there is no pressure.

Question 169

Hoop stress formula

Answer 169

If the cylinder’s wall is >(1/10)*diameter then σ = pr/t where t is the thickness, p is the pressure, and r is the radius

Question 170

Thick walled cylinders

Answer 170

These are cylinders where the wall is thicker than (1/10)*diameter so that the hoop stress within the material varies with radial position.

f= [(r_i² + r_o²)/(r_o²-r_i²)] = inner σ/internal p = σ/p

Question 171

Buoyancy force

Answer 171

This is the force of the displaced fluid. It acts through the center of gravity of the displaced fluid in the up direction

Question 172

Steps to solve: dams and gates

Answer 172

1. ) FBD
2. ) find all relevant weights, hydrostatic forces, and buoyant forces and the places that they are acting on the other object.
3. ) summate forces to find reactions
4. ) summate moments to find positions

Question 173

Bernoulli’s theorem

Answer 173

if a fluid is both inviscid (frictionless) and incompressible

then E= (P/γ) + z + V²/2g

Question 174

Energy Equation

Answer 174

The energy equation is the equivalent to bernoullis when there is head loss or energy is added to the system. To use identify to place where the system has less energy to add loss. Head loss and power is in terms of feet of energy.

(P₁-P₂)/γ + (z₁-z₂) + (V₁² - V₂²)/2g = H_L - H_p

Question 175

Head loss due to friction

Answer 175

Frictional head loss is proportional to the length of the pipe. Inversely proportional to the diameter to some power because SA = f(d²). Varies as a function of the roughness of the pipe and flow turbulence. Varies with velocity like solids but is independent of pressure.

h_f = f (L/d) (V²/2g) where L is the pipe length, f is the friction factor, V is the average velocity ( ∫ V dA/ ∫dA)

Question 176

Orifice coefficients

Answer 176

This is a result of the vena contracta effect where the change in momentum causes the discharge of flow to have a smaller diameter than the outlet. The smallest diameter in comparison to the orifice diameter is related by the coefficient of contraction.

Question 177

How to use the coefficient of contraction

Answer 177

C_c = smallest area of jet/ area of orifice

Question 178

Q for fluids

Answer 178

Q is the volumetric flowrate given in ft³/s

Question 179

velocity from a orifice

Answer 179

V = C_v [2gh]^.5 where C_v is the velocity coefficient (usually .98) and h is the distance from the free surface to the discharge.

This only works if there is not a turbine or other thing being moved by the flow.

Question 180

Minor losses

Answer 180

These are losses due to changes in the geometry of the flow (conservation of momentum requires external forces)

H_L = Σ k_sys (V²/2g)

Question 181

Viscosity

Answer 181

The viscosity of a fluid is defined by its internal resistance to flow.

Question 182

dynamic viscosity

Answer 182

This is the ratio of applied shear to the change in velocity throughout a fluid.

μ = τ /(dV/dy) where y is the vertical distance from the stationary surface to the point of interest within the fluid.

Question 183

Kinematic viscosity

Answer 183

This is ν = μ/ρ and has units of L²/s. It represents the viscosity of a fluid without relating it to the density of the fluid.

Question 184

Newtonian fluids

Answer 184

These are common fluids where viscosity is independent of shear.

Question 185

non-newtonian fluids

Answer 185

for a non-Newtonian fluid the viscosity depends on the rate of applied shear such that it becomes more viscous as the shear increases

Question 186

Reynolds number (pipes + open channels)

Answer 186

Pipes: Re = ρVd/μ = Vd/ν

Open channels: VL/ν where L is the characteristic length

The reynolds number is related to whether a flow is considered turbulent or laminar which dictates whether the flow lines of the fluid move in parallel or at random.

Question 187

pump head for a pump moving a material to a resivor with a higher z

Answer 187

Work/ γ * Q = (z2-z1)+(P2-P1)/γ + (V₂²-V₁²)/2g +h_l

Where: h_l = f(l/D)(V²/2g) where V is the V exiting the pump and throughout the pipe of length l and diameter d

hl can also be minor losses with are equal to the summation of the loss coefficients times V²/2g

Question 188

What is Q

Answer 188

Q is the volumetric flow rate it is given in cubic feet/sec

Question 189

How to solve multi-pipe problems

Answer 189

1. ) draw diagram and ID end states for P, V, Z, l, and D + unknowns
2. ) write energy equation from 1->2 , 1-> 3… where h_L = f₁(l₁/d₁)(V₁²/2g) + f₂(l₂/d₂)(V₂²/2g) + minor losses. This is added to the second state of the fluid.
3. ) Conservation of matter says that Q_in = Q_out
4. ) Solve

Question 190

Pitot Tube

Answer 190

This is a L-shaped tube that measures the stagnation pressure of a moving flow. If we consider h to be the difference in heights of a fluid in a pitot tube and a static pressure tube (vertical tube) then V_flow= [2gh]^.5

Question 191

Venturi Tube

Answer 191

This is a tube for measuring the velocity of a flow that uses a differential pressure across a contraction.

For the formula A₁>A₂ and P is measured through h of the fluid where h=P/γ

Question 192

Flow over weirs

Answer 192

weirs are notched openings in vertical gates.

H=height from the crest to the level upstream surface= energy head of weir.

To solve weirs be aware that the velocity is proportional to the height of the flow and that the vena contracta effect influences the flow.

Question 193

Sluice gates

Answer 193

These are gates where the flow is moving out of the bottom of the tank, under the gate.

Question 194

Solving sluice gates

Answer 194

1. ) Draw FBD
2. ) label end states where 1 is on the top of the resivoir and 2 is on the top of the outer flow and datum is given at the ground.
3. ) apply Bernoulli’s equation or the energy equation

Question 195

Force on an object redirecting fluid

Answer 195

F_x = ρ (ΔV_x ) with an equal for F_y

V₂ is found through conservation of mass

Question 196

Current; symbol, units, meaning

Answer 196

Current, I, is a measure of the flow of electric charges in a conductor.

It is given in amperes which is related to the number of mols of electrons that are flowing through the cross-sectional area of a wire

Question 197

Charge: Units, symbol, meaning

Answer 197

Charge, Q, is the total current over a one second time interval

Amps= Coloumbs/second

Q=coloumbs which are proportional to the mols of electrons

Question 198

Electromotive force (EMF)

Answer 198

This is given in units of Volts, V, and is related to the difference in potential energy. It causes for current to flow.

Question 199

Resistance: units, meaning, symbol

Answer 199

Restitance, R, is the discrete resistance to current and arises from the physical characteristics of the material that current is flowing through.

It is measured in ohms, Ω

Question 200

Capacitance; what is it, units, and symbol

Answer 200

Capacitance is a measure of how well two conductive materials separated by an insulator hold charge. It is measured is Farads, F

Question 201

Inductance

Answer 201

Inductance is a measure of property of a coil to create an EMF that opposes the net flow of current through the coil. It is given by the symbol L and is measured in henrys H

Question 202

Energy: what is it, symbol, and units

Answer 202

Energy is considered to be the amount of work a system is capable of doing on another object. This is measured is Joules where 1 joule = 1 N*m because Work = F X d

Question 203

Power: What is it, units, and symbol

Answer 203

Power is the rate of doing work. It is measured in Watts where 1 W = 1 J/s

Question 204

Horsepower

Answer 204

This is a type of power where 1 hp = 746 W = 2546 btu/hr

Question 205

Efficiency: what is it, units, and symbol

Answer 205

For electrical systems efficiency is given by μ = (Power delivered to load)/(Power Generated) = P_o / P_i it is measured as a percent

For mechanical pumps and things μ = (Power produced - loss)/(power produced)

Question 206

Regulation: What is it, Units, and symbol

Answer 206

This is efficiency for voltage defined as:

(No load V - Full load V)/(Full V) and given as a percentage

Question 207

Gram-calorie

Answer 207

This is the energy required to raise the temperature of 1 gram of water 1 degree centigrade measured in joules and dependent of the specific heat of the material in question.

Question 208

what units are milli

Answer 208

10^-3

Question 209

units of Mega

Answer 209

M = 10⁶

Question 210

Micro units

Answer 210

μ = 10^-6

Question 211

Units of pico

Answer 211

p = 10^-12

Question 212

kilo

Answer 212

k = 10³

Question 213

Giga

Answer 213

G = 10⁹

Question 214

Coulomb’s Law

Answer 214

This says the mutual force acting between two particles is given by the electrostatic force:

F = kq₁q₂/d² where k ~ 9*10⁹ Nm²/C²

q is the charge of each particles in coulombs where oppositely charged particles attract

Question 215

Electric Field intensity/magnitude

Answer 215

This is the idea that is we were to have some charged particle and then we place a positive charge in its vicinity that it would experience a force/coloumb of positive charge given by

E = F/q₁ =N/C

Question 216

Electric field direction

Answer 216

This will depend on the charge of the particle/s but if only one particle is present the direction is radial to the charge. If more than one is present you can break it into two+ systems and add vectors.

Question 217

Conductors/Insulators

Answer 217

These are concepts for different materials that behave differently when current flows through them. Metals are conductors because their large shells and abundant valence electrons allows them to transfer charges easily. Insulators are generally materials that have small orbitals and less discrete ways to transfer charge.

Question 218

Ionic substances for charge

Answer 218

Ionic substances when in solution or as a molten solid are great conductors because the charge can “bounce” between atoms but as solids they are very poor conductors because charges are within the tight inner bonds.

Question 219

Semiconductors

Answer 219

These are materials that act as insulators when the voltage across the material is less than the threshold value which prevents charge from flowing through the system. Above the threshold value this shifts.

Question 220

Factors influencing resistance

Answer 220

These include things like heat, humidity, and other

Question 221

Faraday’s Law for electrolysis

Answer 221

This is a law relating the amount of dissolved or precipitated material in an electrolytic cell as a function of the charge flowing through the system.

If you find: (atomic mass/valency) that is the total mass of a substance that would change if 96500 coulombs passed through the system.

then: (mass/valency/96500) = (mass change / # coloumbs)
and: Q (coloumbs) = I * t

Question 222

Faraday: unit, what is it

Answer 222

This is a convenient way to group coloumbs (charge). it says that one faraday = 96500 coulombs

Question 223

Calculating resistivity of a circular conductor

Answer 223

R= ρ L/A where:

ρ = CM*Ω / ft ; CM = circular mils (1 mill = .001 in) ; A= d² where d is the wire diameter in cm ; L = wire length in feet

Question 224

change in resistance due to T

Answer 224

R₂ = R₁ (1+ α dT) where α = temperature coefficient

Question 225

Rankin

Answer 225

^oR = ^oF + 459.67

Question 226

Resistance at absolute zero

Answer 226

electrons do not flow at absolute zero (in theory)

Question 227

Kelvin

Answer 227

^oK = ^oC + 273.15

Question 228

farenheight to celsius

Answer 228

^oF = ^oC*(9/5) + 32

^oF is always greater than Celsius

Question 229

resistance in series

Answer 229

R_EQ = Σ R_i

Use this to combine resistors in parallel and simplify circuits

Question 230

Resistance in parallel

Answer 230

1/R_eq = Σ 1/R_i or R_eq = 1/Σ(1/R_i)

Question 231

Conductance

Answer 231

This is simply the inverse of resistance given in siemens, G

G=1/R

Question 232

G in series and in parallel

Answer 232

Conductance acts opposite to resistance so

G_series = 1/(Σ 1/G_i) and G_parallel = ΣG_i

Question 233

Calculating conductance

Answer 233

For parallel plates separated by a diaelectric

C (farads) = K*∈*A*(n-1)/d

where: K = diaelectric constant

∈ = 8.85 * 10^-12 C²/N*m²

d = plate seperation

A = area of ONE plate

n = # of plates

Question 234

Equivalent capacitence

Answer 234

Capacitence in a series: C_eq = 1/ (Σ(1/C_i)) because charge is being distributed linearily among the capacitors like how charge is distrubuted among resistors

Capacitence in parallel: C_EQ = Σ C_i This is because the charge can be transfered between lines

Question 235

Equivalent inductance

Answer 235

In a series: L_eq = ΣL_i because charge flows through each inductor like resistors

In parallel: L_eq = q/(Σ(1/L_i))

Question 236

Calculating inductance for a coil

Answer 236

L (henrys) = N²μ A/l

where μ = constant of magnetic permeability

l = avg length of form

A= cross sectional area of hypothetical cylinder within the coil

Question 237

DC circuits

Answer 237

Within a closed DC circuit current flows in one direction from the positive to negative battery terminal

Question 238

Ohms law

Answer 238

V = I*R where voltage is the potential energy difference across the resistance. I is the charge flowing through the resistance and R is the amount of resistance

Question 239

Kirchoff’s Rules for closed electrical systems

Answer 239

Σ I_in = ΣI_out where I is the current flowing in and out of a node which is just an intersection of wires. This represents the conservation of charge/matter.

AND

Σ V_rise = Σ V_drop where V is the voltage found through “walking the circuit” This represents the conservation of energy

Question 240

Current division rules

Answer 240

This represents the distribution of current throughout parallel resistors and is given by I₁ = R₂*I/(R₁+R₂) and I₂ = R₁*I/(R₁+R₂)

Where I₁ and I₂ represent the current flowing through the resistor of the same subscript. I = ΣI₁ + I₂ and represents the total current distributed through the parallel resistors

Question 241

Voltage division rules

Answer 241

This is for resistors in series where V₁ = R₁ * V/(R₁ + R₂) and vice versa for V₂ where V is the total voltage drop

Voltage across parallel resistance is equal among each of the resistors.

Question 242

AC current

Answer 242

This is alternating current where V=f(t) and V(t) = V_psin ωt

where ω = radians/sec and represents the angular frequency of the AC

V_p= peak voltage at which V(t) is oscilating between

Question 243

Converting from frequency to angular frequency

Answer 243

ω (rad/sec) = f*2pi = (1/s)*rad

Question 244

Root mean square voltage

Answer 244

This is the weighted average voltage given by

V_RMS = [(1/T) ∫₀^t V(t)² dt]^.5 = V_p/2^.5 = .707 V_p because the integration is based on a 2pi cycle where T is the period (s) V_p = peak voltage

Question 245

DC V conversion

Answer 245

V_dc = (1/T) * (∫₀^t V(t) dt) = 2V_p/pi = .637 V_p

where t is chosen to equal 1/2 a full cycle (ωt = pi)

Question 246

Using AC in diagrams

Answer 246

Just plug V(t) in for V in all of the other formulas

Question 247

What does I_rms represent?

Answer 247

This represents the effective current moving through a resistor. This represents the current that would effectively flow through a resistor at time=t for a DC current

Question 248

Lead and lag

Answer 248

The current and voltage over time in sin/cos space are related by the phase angle which represents which is “ahead” of the other in time.

if for voltage the phase angle > 0 then it is a phase lead

Question 249

Defining a function (V -> V_rms ->phase space)

Answer 249

If given V= V_p *sin(ωt+θ) then V_rms = .707 V_p and can be represented in polar as V_rms (θ) which translates to a rectangular vector given by

a+bi = (V_rms *cosθ)+ (V_rms *sinθ)*i

Question 250

Impedence

Answer 250

Now that we have a bunch of imaginary numbers plain logic doesn’t work so we have Z=impedance = V/I where V=Vrms and I=Irms as complex numbers (remember in DC that R=V/I)

Question 251

Capacitance with impedance

Answer 251

Capacitance causes the voltage to lag the current by 90^o where

I = ωCV_p cos(ωt) = V_p/(1/ωC) * sin(ωt+90)

Question 252

Voltage across a capacitor

Answer 252

V_p sin(ωt) = ∫₀^t i(t)/c d(t) where C is measured in farads

Question 253

Lenz’s Law

Answer 253

V(t) = -L d(i(t))/dt

Question 254

how to use Lenz’s law

Answer 254

Seperate d(i(t)) from dt and solve for i(t) by integrating ∫ d(i) = ∫ V(t)/L dt

Question 255

Power average DC

Answer 255

P_avg = V²/R (watts) where V = V_dc

Question 256

Power Avg AC

Answer 256

P_avg = Vr_msI_rms

Question 257

Real, reactive and apparent power

Answer 257

Power =VI which has real and non-real (imaginary) components which can be written in vector space.

Apparent power = S = magnitude

Real power = VIcosθ in watts

reactive power = VIsinθ in VARS

Question 258

Loop method

Answer 258

When there are many meshes you can assign each a loop current (I₁, I₂…) and find the total voltage drop through the loop. When using this method always move counter clockwise and when wires are shared use V=R(ΣI)

Question 259

Parallel resonance (RLC)

Answer 259

The resonant frequency, f_o, represents the frequency at which Z=Z_o =Z_max

f_o = 1/2pi[LC]^.5 where Z_o = L/CR =Q²R and I_t = V/Z_o

Question 260

Series resonance

Answer 260

f_o (hz) = 1/2pi[LC]^.5

Question 261

Bandwidth

Answer 261

This is the frequencies for AC where P and I are >.707 max

Question 262

Filters

Answer 262

These are networks designed to discriminate frequencies of signals. A pass band creates constant amplitudes whereas a reject band has a low amplitude response.

Question 263

attenuator

Answer 263

This is a network that is designed to isolate one network from another preserve a match between networks.

Question 264

Three Phase Power

Answer 264

This is fundamentally based on the concept that if you have three voltages each 120^o from one another the time weighted average is equal to V_RMS and can be used to power systems like motors without as much vibration.

Question 265

Delta circuit

Answer 265

This is where there is a three phase delta load connected to a delta power source where Z is between nodes.

In these systems the V_line = V_AB=V_BC=V_CA but the phase currents (I_CA, I_CB, I_AB) are equal to 1/([3]^.5) * I_L

and in a balanced system P = [3]^.5 V_L*I_L

Question 266

Finding line currents in three phase power with phase currents

Answer 266

Line currents are the currents delivered to the loads (A,B,C) and are denoted by either I_L or I_A,B,C… where I_B = I_BC- I_AB and so on where the rule is that the inner subscripts of the numbers cancel each other out

Question 267

total power in three phase delta system

Answer 267

P_T = summation of all lines (V_AB²/Z_AB)

Question 268

Wye three phase circuit

Answer 268

This is a circuit with a Y configuration that is similar to a delta configuration but it is not balanced so it has a N wire (neutral) at the core.

Question 269

Currents and loads in a Y system

Answer 269

In a wye system line currents are equal to one another and the neutral.

Question 270

Phase voltage in a Wye system

Answer 270

V_coil = V_L/[3]^.5 where V_L is measured from the node to nuetral.

Question 271

Power in a wye system

Answer 271

This is the same as a delta system

P = [3]^.5 V_L I_L cosθ

Question 272

Magnetic circuits

Answer 272

This similar to an electric circuit where

Resistance = Reluctance

Magnetic force = voltage

flux flow = current

Question 273

magnetic reluctance

Answer 273

This is like resistance for a magnetic circuit and is given by R = L/μA where μ is the magnetic permeability constant of the core of the material, L is the mean length, and A is the cross-sectional area

Question 274

Current density

Answer 274

This is a measure of the density of magnetic field lines given by

B (teslas) = ϕ/A = μH

Question 275

Field intensity for magnets

Answer 275

H = t/L = t/2pi r

Question 276

Transformers

Answer 276

These are electromagnetic devices that consist of one or more coils that is used to “step up” or “step down” voltages for various uses. They are generally rated in KVA or VA where a 100 KVA transformer can deliver 100KW of power if pf = 1

Question 277

Turns rule for transformers

Answer 277

This says that V₁/V₂ = I₂/I₁ = N₁/N₂ = a

Question 278

Impedence loading through transformers

Answer 278

If we have a transformer with I₁ and Z_i represents the impedence from the coils with a Z₂ = load related to the other side of the transformer with I₂ then it is said that Zi = a² Z₂ where a = N₁/N₂

This is also referred to how much of the load is reflected into the primary.

Question 279

Short Circuit tests for determining transformer character

Answer 279

A transformer is loaded with the various electrical character for which it is rated and then on the primary an ammeter, wattmeter, and voltmeter are attached. An ammeter is attached to the secondary.

copper losses = wattmeter rating = losses from within the primary coil

Equivalent impedence = Z_eq = V/I₁ where I₁ and V are measured by the ammeter and voltmeter respectively

Equivalent Resistence = R_eq = W/I₁²

equivalent reactance = X = [Z² - R²]^.5

Question 280

Losses within a transformer

Answer 280

These are similar to any coil where there are

1. ) copper losses which refers to the heat that is created in the copper
2. ) core loss related to eddy currents and hysteresis

Question 281

Per-Unit Notations

Answer 281

This is definition oftentimes applied to electrical equipment to normalize quantities to a common base. This basically says that there are relative values of electrical properties within the equipment

Base current (amps) = base KVA/ base KV

Base Impedence = base voltage/ base current = (base voltage KV)²*10/ base KVA

Question 282

Ways to test transformer properties

Answer 282

1. ) short circuit test
2. ) open circuit test

Question 284

General menaing of current

Answer 284

When stated to find current this means the line current.

Question 285

general meaning of voltage

Answer 285

This means finding the volts to nuetral and KVA per phase

Question 286

Autotransformer

Answer 286

This is when there are more than one coils serially connected usually in a way that there is a winding abc with a load parallel to bc.

Question 287

What does N₁ equal in an autotransformer?

Answer 287

N₁ = winding abc (the full winding) and N₂ = the winding parallel to the load usually winding bc

Question 288

a = ? for an autotransformer

Answer 288

a = V₁/V₂ - I₂/I₁ + N₂/N₁ and I through the second winding is given by I_t-I₂

Question 289

Rotating electrical machines working principle

Answer 289

All rotating electrical machines operate on the principle of electromagnetic induction such that whenever there is a change in the magnetic flux there is an induced electrical force.

Question 290

Faraday’s Law

Answer 290

This says that whenever there is a change in magnetic flux an emf is produced and is given by

e= - d(Nϕ)/dt where Nϕ is the magentic flux through a closed loop that has current flowing through it.

Question 291

Magnetic Flux

Answer 291

This is measured by ϕ and is given by B X A where B is the magnetic field and A is the loop such that if the loop is perpindicular to the main field that ϕ_max is achieved

Question 292

Right hand rule for F, B, and I

Answer 292

For a loop with current, I, within a magnetic field, B the force on the loop is given by your thumb, your pointer is in the direction of the magnetic field, and I is the direction of your middle finger such that F = B X I

Question 293

Torque for an electromotive moter

Answer 293

This is given by T = ϕ_maxI sin ωt where ωt is a term relating the rotation of the coil to radians because F = B X I where B is given by ϕ

Question 294

DC motors function

Answer 294

This is relatively similar to an AC motor but there is a commuttor attached to the loop so that way the direction of current switches ever pi radians. This has the effect of keeping the net current unidirectional and is in the function of a abs(sin ωt) where ω is proportional to the angular frequency of the coil

Question 295

How to reduce jittering in a DC motor

Answer 295

With one loop the DC current oscilates between 0 and max every pi radians. With multiple loops you can have lead/lag @ 120^o or other to stabilize the avg voltage across the loop

Question 296

Commercial generator operation

Answer 296

This generally has many distributed N-S poles throughout a cylinder that maximizes the flux throughout the entire rotating and prevents the coil from being stagnate because it will never reach a stable equilibrium where it can be perturbed with changing phase.

Question 297

AC generator function

Answer 297

This is very similar to a DC generator but has slip rings not a commutor so that way voltage/current oscilates in both positive and negative space

Question 298

frequency of an AC generator

Answer 298

f = pN/2 where p is the number of poles, N is the rev/sec of the mechanically driven loop (gas powered)

Question 299

power factor

Answer 299

This is the ratio of usable power to total power.

Synchronous motors have a leading power factor

Question 300

Time domain analysis in electrical systems: idea

Answer 300

This is the idea of using diff eq to solve for various parameters of RLC circuits where the beginning and end states are known and we are solving for the middle period.

Generally: t₀ = the time when a switch or something is turned on

t₁= steady state when either there is not a fluctuation in the electrical parameters or there is nothing occurring. This is usually at infinity

Question 301

What are the three primary physcial components in an time domain analysis problem?

Answer 301

These are usually RLC circuits which include a resistor, inductor, and capacitor.

Only the resistor does not instantly change with t. Inductors and capacitors store charge so that when there is a change in the state of the system they do not instantaneouslt shift to the final state.

Question 302

Inductors

Answer 302

These are coils that having current flowing through them. The moving charges induce a magnetic field with the positive end in the direction of the entering current

Question 303

Energy stored within an inductor

Answer 303

The energy stored within an inductor is given by W = (1/2)LI² where W=joules, L=inductance (Henrys), and I = current (amps)

Question 304

Voltage across an inductor

Answer 304

This is related to time and inductance by V_L = L di/dt where the positive voltage is in the direction of the current entering the coil. If there is not a change in the current across an inductor than the induced voltage is 0.

Question 305

Voltage across an inductor with time

Answer 305

Because V_L = di/dt L if we have i drop to 0 in dt~0 then V_L= infinity. In the situation where the source is removed then the inductor become a source where current is generated as given by lenz’s law to oppose the change of current within the inductor

Question 306

Capacitors

Answer 306

These are effectively a series of parallel plates that accumulate charge proportional to the surface area of the interfacing plates.

Question 307

Power within a capacitor

Answer 307

This is given by W = (1/2) CV² where W = joules, C = capacitence (Farads), V = V_c across the capacitor

Question 308

current flow through a capacitor

Answer 308

This is given by the relationship i_c = C (dV_c/dt) therefore in a DC circuit where dV/dt = 0 the capacitor acts like an open circuit and there will not be any current flowing across the capacitor

Question 309

Total/Complete Response

Answer 309

This is the description of an RL or RC circuit within a changing state. It is said that there are two sources of energy, the natural response refers to the internal response of either a capacitor or a inductor. The forced response is the induced response given by an external forcing like a battery or generator. This is also called the steady state response because it is the function that describes the system if closed at t=infiinity.

Question 310

how to solve a transient state problem

Answer 310

Because there are generally two forces that are influencing the system; the natural and forced responses we can independently analyze each response then add them together to find the complete response.

Question 311

dRL circuits at t = 0⁺ (closing switch)

Answer 311

via Kichoff’s voltage law L (di/dt) + Ri = V where i = i(t)

i_n= K e^{-R<span> </span>/L} where K is determined from the conditions at t=0 and i_n(t) is the natural response. K = V/R

i_ss = V/R = steady state

i(t) = (V/R) (e^{-R/L * t} + 1)

Question 312

RC circuits

Answer 312

These are circuits that have resistance and a capacitor connected to a source. Because electrons are matter they do not instantly accumulate onto the capacitor therefore when connected to a source there is a natural and forced response

Question 313

complete response of an RC circuit

Answer 313

by KVL: V_r + V_c = V_s

i_t = (V/R) e^{-1/RC * t} V_c= (1/C) Ve^{-1/RC * t} V_r= - V e^{-1/RC *t}

Question 314

Systems

Answer 314

This can be described as a combination of diverse interacting elements that are integrated to achieve one objective.

Question 315

Systems engineering perspective

Answer 315

This is the idea of looking at all of the interacting elements and evaluating if the system reaches its objective. Systems engineers do not care about design only outcomes.

Question 316

open loop automatic control system

Answer 316

This is a system where the output has no effect upon the input.

This is basically y=f(x) where y, the output, only depends on the input, x

Question 317

closed loop (feedback) control systems

Answer 317

This is where the outcome of an input is fed back into the component to alter future outputs.

It is similar to saying y = f(x,t) where the output, y, is not only a function of the input, x but also is influenced by time. In this specific instance with time the prior y values are used to change future y values.

This means that y(x₁, t₁) =/ y(x₁, t₂) even though the input is the same

Question 318

On-off controllers

Answer 318

This is a closed system where the system is turned on/off if the error signal is a certain value. This is like a thermostat.

Question 319

Step controllers

Answer 319

This is a type of on-off controller where the error signal varies the magnitude of the output. For example in a furnace, if the error signal returns that it is very cold then it may overshoot the desired temperature.

Question 320

Servomechanisms

Answer 320

These are closed loop systems where the output is measured in comparison to a reference and the power to the system not only varies in magnitude but information to change the output. For example the autopilot on a plane tracks the course of the plane in reference to the ideal and uses that to create an output that varies velocity.

Question 321

Standard block diagram symbols/nomenclature

Answer 321

See chart given but a few notable symbols include

v = the independent input

b = feedback variable

r = reference input = f(b, v) and is the signal the component uses

e= r-b = actuating signal = the error

c = controlled variable; the measured variable; the output

G_v = reference input elements

G = dynamic unit; both control systems and components

H = feedback elements; the components

Question 322

Differential equation method of system analysis

Answer 322

This is the method of describing the feedback system through implicit differentiation and series expansion. These are best for quantized systems where products or discrete values that can be returned into the function.

Question 323

Transfer functions of feedback control systems

Answer 323

This basically uses a laplace transformation of a differential equation to interpret the magnitude, phase, and phase of a system.

Question 324

Semiconductors

Answer 324

Semiconductors in a pure sense include silicon and germanium. Both have 4 valence electrons and are covalent

Question 325

Intrinsic semiconductors

Answer 325

This includes germanium and silicon and represent a group of materials when, at a certain temperature, the covalent bonds break down and the valence electrons are excited into the conductance band and leave a hole. The combination of these is called an electron hole pair

Question 326

Extrinsic semiconductors

Answer 326

This is the idea of creating impurities in the crystal lattice that either enhances the ability for electrons to shift position or stifles it. These are the extrinsic semiconductors.

Question 327

N-type semiconductors

Answer 327

These are extrinsic semiconductors that are doped with elements that have 5 valence electrons so that the fifth electron is in the conductance band. Because these semiconductors carry more electrons they are considered to be negative thus the name N-type.

Question 328

P-type semiconductor

Answer 328

These are semiconductors that are doped with a trivalent atom so that there are electron vacancies that can then be filled. An example of this is placing Al within silica or germanium

Question 329

minority carriers

Answer 329

This is the idea that at certain temperatures and under certain conditions the materials meant to insulate (silica and germanium) may break down and begin to conduct these are known as minority carriers

Question 330

The P-N junction

Answer 330

This is the junction between the positive and negative material. These are unidirectional interfaces of flow.

Question 331

diffusion current

Answer 331

This is the idea that at the interface of the positive and negative charges that there is diffusion of electrons from the negative to the positive.

Question 332

Depletion region

Answer 332

This says that because of diffusion across the P-N boundary that the negative material will gain many positive charges and the P material will fill its vacancies. They become saturated and there is a depletion region where flow is not occuring. The potential across this is significant.

Question 333

Semiconductor diodes

Answer 333

These are simple devices with a P-N junction

Question 334

forward bias

Answer 334

This is defined as the positive charge of the battery pushing current into the positive end of the terminal. It requires a significant voltage for current to flow.

Question 335

Reverse bias

Answer 335

This is when the negative end of the battery is connected to the negative side of the semiconductor so that the depletion area becomes larger and only the minority carrier carry material. This current is called the reverse saturation current, I_s.

Question 336

Period or Series on the Periodic table

Answer 336

These are the horizontal rows on the periodic table. The row indicates the number of energy orbitals for the row.

Question 337

Group or Family

Answer 337

These are vertical rows on the periodic table. Groups indicate the number of valence electrons for all elements in that row.

Question 338

What does the atomic number represent?

Answer 338

These are the total number of protons within an atom.

Question 339

Atomic mass meaning

Answer 339

This is the weighted average of the proportions of isotopes of that atom commonly found in nature.

Question 340

Isotopes

Answer 340

These are molecules with the same number of protons but different numbers of nuetrons which changes their mass.

Question 341

STP

Answer 341

0 ^oC ; 273 ^oK ; 32 ^oF @ 760 mm Hg; 1 atm; 2116.2 psfa

Question 342

mole/pound Molecular Volume

Answer 342

This is the molecular volume of a gas at STP. For any gas @ STP this is 22.4 liters/mole of gas.

In imperial this is 359 ft³/pound of gas.

This also says that if we have a 22.4 liter container of 1 mole of gas @ STP it will exert 1 atm of pressure

Question 343

Gay-Lussac Law

Answer 343

P₁/T₁ = P₂/T₂

This says that the pressure of a given mass of gas within a fixed volume is linearily related to the temperature of the gaseous volume

Question 344

Avogadro’s Number

Answer 344

This says there are 6.024 * 10²³ molecules/mol

Question 345

Ideal Gas Equation

Answer 345

PV = nRT

where P = abs pressure; V = gaseous volume; T=^oK

n= moles; R=.082 l * atm/mole*K

Question 346

Graham’s Law

Answer 346

This says that the rate of diffusion (r) between two gasses is inversely proportional to the square root of the gas density/molecular weight

r₁/r₂ = [ρ₂/ρ₁]^.5 = [m₂/m₁]^.5

Question 347

Dalton’s Law of Partial Pressures

Answer 347

This says the sum of the partial pressures of each gas is equal to the total pressure of the mixture

P_T = Σ P_i

Question 348

Synthesis Reactions

Answer 348

These are reactions that produce one product from 2+ reactents

Question 349

Decomposition Reactions

Answer 349

These have one reactant that decomposes into several products

Question 350

Single Displacement Reactions

Answer 350

These are reactions where one more reactive atom replaces a less reactive atom to create a lower PE state

Ex: Zn + 2HCl -> ZnCl₂ + H₂

Question 351

Ion Exchange Reactions

Answer 351

These are reactions where there is a double displacement of atoms. It commonly represents the neutralization process between acids and bases.

AB + CD -> AD + CB

Ex: NaOH + HCl -> NaCl + HOH which works because NaCl is in a low PE state as an ionic compound and HOH is a strong hydrogen bond

Question 352

Reversible Reactions

Answer 352

These are reactions that go either direction and do NOT go to completion because there is a constant system perturbation as long as all products and reactents remain in close proximity.

Question 353

Equilibrium condition of a reaction

Answer 353

This is when the rate of forward reaction = rate of reverse reaction. Also known as dynamic equilibrium

Question 354

Law of Le Chatelier

Answer 354

This says that when a system in dynamic equilibrium is subjected to a stress that the system shifts so the stress is relieved and dynamic equilibrium is restored.

Question 355

How does pressure influence the dynamic equilibrium of a gaseous reaction?

Answer 355

An increase in pressure will favor the smaller volume product/s or the side of the reaction with less separate molecules.

Question 356

Dynamic Equilibrium with a change in concentration/quantitu

Answer 356

With a shift in the concentration of materials the other side of the reaction is favored

Question 357

How does dynamic equilibrium shift with temperature?

Answer 357

With an increase in temperature the endothermic product is favored, with a decrease in temperature the exothermic reaction is favored.

Question 358

How do catalysts shift dynamic equilibrium?

Answer 358

Catalysts lower the PE barrier to reacting therefore a catalyst equally increases the rate of both the forward and backwards reaction.

Question 359

Equilibrium Constant Formula

Answer 359

For some reaction given by WA+ZB <=> XC + YD at a position where R₁ = R₂ and [] = molarity of the substance (moles/L)

K_eq = [C]^x [D]^y/ [A]^w [B]^Z

Question 360

K_eq meaning

Answer 360

K represents the proportion of products and reactants at equilibrium

If K>1 then the forward reaction (exothermic) is favored

If K=1 then neither product or reactants are favored

If K<1 there are more reactants than products and the reverse reaction is favored

Question 361

What is Q

Answer 361

Q = K but when the reaction is not at dynamic equilibrium

Question 362

Ionization Constants

Answer 362

These are K_eq for the ionization of different acids. The larger the ionization constant the more stronger the acid or base is.

HA_a + H₂O <=> H₃O⁺ + A_a^-

Question 363

The solubility Product

Answer 363

This shows the solubility of slightly soluble salts where the large the solubility constant, the more soluble the salt

AB_s <=> A⁺_aq + B^-_aq

Question 364

Solids within K calculations

Answer 364

The molarity of a solid is 1

Question 365

K for H₂O <=> H⁺ + OH^- ?

Answer 365

This is K_w aka the water ionization constant which is equal to 10^-14

This means that within 10⁷ liters of water there is one mole of OH and H because K_w = 10^-7 * 10^-7

Question 366

pH formula

Answer 366

pH = -log[H⁺] thus a smaller pH is a more acidic solution

Question 367

Relationship between pH and pOH?

Answer 367

pH+pOH=14

Question 368

What does a pOH of 1 mean

Answer 368

This means that at equilibrium, the substance has a molarity of 10^-2 for OH or 10^-2 moles OH/L meaning that it is a very basic liquid

Question 369

Percantages in a solution

Answer 369

This is the number of units of weight of material is in 100 units of weight of the solution. It is a form of PPM.

Question 370

Molarity

Answer 370

M = moles of solute/litre of solution

1M means that in a solution with a total final volume of 1 litre that 1 mole of solute has been added.

Question 371

Normality

Answer 371

N = # of equivalents/litres of solution = #of equivalents * molarity

where: # of equivalents is given by the number of moles of a reactent in the equation and the molarity is the other reactent or product in the equation. It is most common for titrations

Question 372

Molality

Answer 372

This is the moles of solute/litres of solution

Question 373

Alpha Decay

Answer 373

This is the spontaneous emission of an alpha particle (⁴He) which decreases the reactent by two protons and 2 nuetrons

Question 374

Beta Decay

Answer 374

This is the spontaneous emission of a beta particle (a nuetron that shifts to an electron) This causes the particle to add a proton increasing its mass number and atomic number by 1

Question 375

Mass relationship to readioactive decay

Answer 375

If we have a mass at t=0 of m_o then m after some t is given by m = m_o e^-δt where δ = decay constant

Question 376

t_1/2 = ?

Answer 376

t_1/2 = ln2/δ = .693/δ and represents the amount of time that it takes for half of a radioactive species to decay

Question 377

Definition of one calorie

Answer 377

This is the amount of energy needed to raise the temperature of 1 gram of water by 1 ^oC

Question 378

The heat of fusion

Answer 378

This is the energy required to break the bonds of a solid as it is transitioning to a liquid even though the temperature does not shift.

Question 379

Heat of fusion for water

Answer 379

it takes 79.7 calories to melt 1 gram of ice

Question 380

Heat of Vaporization

Answer 380

This is the amount of energy needed to change the phase of a liquid to a gas. For water this is equal to 539.6 calories/gram. That also means that in the transition from a gas to a liquid that 539.6 calories are released.

Question 381

Bond Energy

Answer 381

This is the amount of energy needed to break the bond of two or more atoms.

Using Hess’s Law the bond energies of each reactent can be used to find the total heat released in a reaction

Question 382

Hydrocarbons

Answer 382

These are compounds solely composed of carbon and hydrogen. They are non-polar, covalent, and insoluble with low melting and boiling points.

The general formula for hydrocarbons is R-H where R= the hydrocarbon with an added hydrogen, H

Question 383

Aliphatic compounds

Answer 383

These are carbon compounds where carbon atoms are arranged in straight or branched chains

Question 384

aromatic compounds

Answer 384

These are carbon compounds where the carbon atoms are arranged into rings

Question 385

Homoogous series

Answer 385

These are a family of hydrocarbons with the same general structure. They also share the same general formula and similar properties.

Question 386

Methane series: Alkanes formula and structure

Answer 386

C_n H_2n+2 Methane is CH₄

Question 387

Saturated hydrocarbons

Answer 387

These are hydrocarbons that are bonded singly to themselves and the H atoms.

Question 388

Unsaturated hydrocarbons

Answer 388

These are hydrocarbons where the carbon atoms do not have all four bonds with other things aka they have double bonds.

Question 389

Ethylene Series: Alkenes-olefin series

Answer 389

Formula: C_nH_2n Ethelyne: C₂H₄ These are unsaturated hydrocarbons and the two carbon atoms have a double bond

Question 390

Acetylene Series: Alkynes

Answer 390

General formula: C_nH_2n+2 Acetylene: C₂H₂

These are considered unsaturated because they have a triple bond between the carbons making them non-polar

Question 391

Benzene Series

Answer 391

Formula: C_nH_2n-6 Benzene: C₆H₆ These are also unsaturated because each carbon is bonded to one other thing

Question 392

Substituted Hydrocarbons

Answer 392

These are hydrocarbons where the hydrogen is replaced by a functional group which determines its properties.

Question 393

Alcohols

Answer 393

General Formula: R-OH

methyl alcohol: CH₃-OH

Question 394

Soaps

Answer 394

These are broadly a metallic salt of a fatty acid. They are made by boiling hydrocarbons with a strong base like NaOH or KOH to form soap

Question 395

Carbohydrates

Answer 395

These are C, H, O compounds where the H:O ration is 2:1

Question 396

Common carbs

Answer 396

Glucose, sucrose, starch, and cellulose

Question 397

Valence

Answer 397

This refers to the number of electrons an atom may gain or lose to create orbital stability

Question 398

Oxidation

Answer 398

This is the loss of electrons. It occurs at the anode (+ side) of an electrolytic cell.

AN OX is Positive

Question 399

Reduction

Answer 399

This is the gain of electrons during electrolysis that occurs at the cathode (negative end) of the battery.

RED CAT is Negative

Question 400

How to balance a redox reaction

Answer 400

1. ) Write half reactions (with electrons) for each of the elements in the reaction
2. ) multiply by coefficients to that electrons balance

Question 401

Oxidizing/Reducing Agents

Answer 401

These are the elements that oxidize or reduce the other element. The oxidizing agent is reduced during the reaction

Question 402

Standard oxidation Potentials

Answer 402

This is a chart with a large number of half reactions of oxidation. A large electromotive potential represents that upon being oxidized the element is in a lower PE state thus it is more favored.

Question 403

Using Standard Oxidation Potentials

Answer 403

To use the E₀ values you summate the associated value with the half reactions created when balancing the reactions.

Question 404

Electrolysis

Answer 404

This is the process of decomposing or recomosing metals through electroplating

Question 405

One Faraday

Answer 405

This is the amount of electrical charge to liberate one gram equivalent weight of an element from solution. One faraday is equal to one mole of electrons.

Question 406

A coulomb

Answer 406

This is 6.24 * 10¹⁸ electrons or other elementary charges. One faraday is equal to 96490 coulombs

Question 407

Boyles Law

Answer 407

This says that pressure and volume of a gas at a constant temperature are inversely related by a linear relationship given by:

P₁ * V₁ = P₂ * V₂ furthermore if dT/dt = 0 dP/dt = 0 and dV/dt = 0

Question 408

Charle’s Law

Answer 408

If the pressure of a gas is held constant then dT/dV = c meaning that any change in temperature has a direct linear change in volume.

Question 409

General Energy Equation

Answer 409

For an ideal, frictionless, steady flow system with dt~0

PE₁ + KE₁ + U₁ + FW₁ + Q_a = PE₂ + KE₂ + U₂ + FW₂

KE = Kinetic Energy = .5 gV²

PE = Potential Engery = z

U = internal heat

FW = work done on/by the system = PV

Q_a = work added to the system

Question 410

Q_a = ?

Answer 410

This is the change in work

Q_a = ΔU + W

Question 411

Is work path dependent?

Answer 411

Yes. Work = W = F x d meaning that if d changes as a vector the work done by/on the system changes.

Question 412

Work for a piston

Answer 412

W = ∫ P dV where P = f(V) for the volume of the piston being closed

Question 413

Specific Heat

Answer 413

This is the amount of energy needed to only increase the temperature of a substance without phase change

If dQ heat is tranfered to a substance with a mass of m the temperature will change by some dT related to the internal character of the material.

In other words C = dQ/mdT

Question 414

How does internal energy relate to specific heat

Answer 414

Q = m*c * ∫ dT

Question 415

k for specific heat is?

Answer 415

k = C_P/C_v where C_P = specific heat when dP/dt = 0

C_v=specific heat when dV/dt = 0

Question 416

Enthalpy

Answer 416

Enthalpy = H

H = U + PV and ΔH (for gases) = m* ∫ C_p dT

Question 417

Entropy

Answer 417

For a reversible tansfer of heat dS = dQ/T

and ΔS = ∫ dQ/T = m C ln (T₂/T₁)

Question 418

Volumetric analysis of gases

Answer 418

For a mixture of gases at some temperature and pressure

B_x + B_y + B_z = 100% where B = V(component)/V_T

Question 419

Gravimetric analysis

Answer 419

G_x + G_y + G_z = 100%

G = m(component)/m_T = V(component)*rho / V_T * rho_T

Question 420

Heating Value of a fuel

Answer 420

This is the amount of heat given up by the products of combustion when cooled to the original temperature that the reactants started.

Question 421

Air within combustion

Answer 421

Assume that air is .77 N₂ and .23 O₂

Question 422

Perfect gas assumption

Answer 422

This assumes that the gaseous atoms have negligible or no volume and has no attractive forces between individual atoms.

Question 423

Vapor

Answer 423

These are gases that are in a state where they can reverse into a liquid state. When vapors are heated to temperatures that far exceed boiling point they are “superheated” and may form a perfect gas.

Question 424

Saturation temperature

Answer 424

This is a thermodynamic term for describing the boiling point for a substance at some pressure.

Question 425

Quality of a wet steam mixture

Answer 425

This is defined as the % of mass that is in a saturated gas state.

Question 426

Throttling calorimeter

Answer 426

This is a device used to measure the quality of a wet steam mixture. Steam’s enthalpy is measured at two points of a tube.

x = h₁ - h₂ / h_fgl

Question 427

Mollier chart

Answer 427

This is a chart that has various enthalpy values for wet steams

Question 428

Relative Humidity

Answer 428

ϕ = P_w/P_g

The relative humidity represents the ratio of the partial pressure of water vapor being the vapor in a superheated state to the partial pressure of saturated vapor at that same temperature.

Question 429

humidity ratio

Answer 429

This the ratio of mass of water to the mass of dry air and given by γ

This is related to relative humidity by = γP_a /.622 P_g

Question 430

How do steam power plants work?

Answer 430

A boiler converts chemical energy into heat which provides high temperature to a prime mover like a turbine or steam engine.

Question 431

Refrigeration

Answer 431

This describes the process of heat being absorbed from a low temperature region which is commonly done through evaporation and decompressing vapors to convert the latent heat into phase changes.

Question 432

Conduction

Answer 432

This is the most common form of heat transfer and is described by

Q = kA(T₁ - T₂) /X where

Q = heat transferred (btu/hr)

A = area through which the heat flows

X = the distance of the heat flow

k = constant that is material dependent

Question 433

maximum nozzle flow is obtained by?

Answer 433

This is a function of the exit pressure for the nozzle. If P₂ < P_c then the flow out of the nozzle will be less than the maximum attainable value.

P_c = critical pressure and represents the optimal exit pressure for the nozzle

If the flow through the nozzle has exit pressures equal to or less than the stagnation pressure then flow is maximized

Question 434

Metallic Structures and alloys

Answer 434

This takes the opinion that metals are crystalline structures that are composed of small composites of metals.

Question 435

Metal strength with particle size

Answer 435

Generally metals with smaller grains are stronger

Question 436

Ferrous Alloys

Answer 436

These are alloys that share basic physical characteristics to iron steel

Question 437

Engineering metals

Answer 437

These are non-ferrous metals like magnesium, zinc, nickel, and aluminum which are metals that recently came into the engineering toolbox

Question 438

Auxiliary metals

Answer 438

These are materials that are often capture in small quantities for use in specialized areas.

Question 439

Precious Metals

Answer 439

These are metals that have commoditized value in the international market.

Question 440

What are the three most common packing structures for a metal?

Answer 440

They are generally face centered cubic, body centered cubic, or hexagonal

Question 441

Strong metals crystalline packing structure

Answer 441

These will generally be body-centered cubic at room temperature and include materials like chromium, iron, moly, tantalum, tungsten, and vanadium

Question 442

Crystal packing structure of ductile materials at room temp

Answer 442

These are most commonly found as face centered cubic like aluminum, copper, gold, iridium, lead, nickel, palladium, platinum, rhodium, and silver

Question 443

What metals are hexagonally packed?

Answer 443

Beryllium, cadmium, magnesium, titanium, and zinc

Question 444

slip in metals

Answer 444

This is the crystalline cleavage of metals along discrete planes. It is proportional to shear. After slip has occurred it is a self-stopping mechanism that results in definite work hardening.

Question 445

Phase diagrams for metals

Answer 445

These are generally eliptic curves where the upper limit is the liquidus the middle has liquids and solids and the base is the solidus line.

Question 446

Lever rule

Answer 446

This says that when in a mixed state of liquid and solid that the %liquid = (S-X)/(S-L) where T = C and X is the specific composition being analyzed

Question 447

How to understand alloys

Answer 447

Alloys are characteristically similar to geologic phase diagrams where there is immiscibility, phase changes, eutectics, and perieutectics.

Question 448

Annealing

Answer 448

This is the process of heating a metal to its critical point to heal any slip or internal deformation. It increases the malleability of the metal

Question 449

Steel

Answer 449

This is a type of ferrous alloy with ~2% carbonaceous material

Question 450

Stainless steels

Answer 450

These have a layer of chromium oxide rich alloy (~10%) on the outer edge which prevents rust.

Question 451

allotropic changes

Answer 451

These are reversible shifts in material properties like structure, eletrical properties, and magnetic properties which occur in iron-carbon alloys at critical points/temperatures.

Question 452

Corrosion

Answer 452

This is the result of chemical reactions between metals and the enviroment

Question 453

Corrosion influences (6)

Answer 453

Corrosion can be caused by

acidity, oxidizing, electrolysis, film formation, agitatition, or temperature

Question 454

Mechanisms of corrosion

Answer 454

Generally acidity and oxidation creates the corrosive enviroment but the rate of corrosion is determined by electrolysis, film formation, agitation, and temperature

Question 455

Film formation

Answer 455

This is the development of an oxidized film that separates the base metal from the corrosive environment. Agitation physically removes this layer and increases the rate at which corrosion occurs.

Question 456

How does temperature influence corrosion?

Answer 456

Generally in chemical corrosion increased temperature increases the extent of the reaction and increases the corrosion

Question 457

galvanic action

Answer 457

This is when there are two metals with different electronegativities that are connected by a conductive medium. The higher electro-chemical potential element will act as the anode and these atoms will go into solution.

Question 458

Stress corrosion

Answer 458

This is a form of material failure due to corrosive and dynamic stresses

Question 459

Fretting corrosion

Answer 459

This is basically corrosion related to the shear of two interfacing metals which is eliminated with proper lubrication

Question 460

Material testing via radiography

Answer 460

Radiography of an alloy can reveal where there are variations in density

Question 461

Material testing via accoustics

Answer 461

These tests act very similar to seismeic scans where changes of material properties across boundaries are reflected and velocity is a function of density

Question 462

Materials testing via magnetics

Answer 462

This uses changes in the ferromagnetic reluctance because of internal heterogeneity to understand the material’s internal structural flaws.

Question 463

How to measure the tensile strength of a metal

Answer 463

These are generally destructive tests that use a pendulum to collide with metal to understand the energy transfer.

Question 464

Thermal conductivity

Answer 464

This is the ability for heat to flow through materials expressed in

Cal/cm² /cm /sec/ ^oC

Question 465

Relative thermal conductivity

Answer 465

These are relative measures of how well heat flows through a material using copper as the base

Question 466

Electrical Conductivity

Answer 466

This is related to the atomic structure and atomic number of materials in a metal.

Conductivity = R = rho L/A ohms

R = resistance, rho = resistivity NOT density (ohm-cm), L = cm, A = cm²

Question 467

Factors influencing thermal and electrical conductivity

Answer 467

In general less valence electrons in covalent or metallic states create lower thermal and electrical conductivity. Impurities, strain, and increased temperature increases the disorder of the lattice and increases the resistance to heat or electric conductivity and this defines some alloys

Question 468

Thermal Expansion

Answer 468

There are two forms of thermal expansion: Linear expansion is the expansion along a central axis and Volumetric expansion is the change in total volume

Question 469

Linear and volumetric thermal expansion equation

Answer 469

L_f = L₀ (1+α(ΔT))

V_f = V₀(1+ α_v (ΔT))

α_v​ ~3*α

Question 470

Denseness

Answer 470

This is independent of weight and refers to the lack of porosity in a material

Question 471

Porosity

Answer 471

This is the quality of a material having voids which enable fluids to be transferred through the material

Question 472

Fusibility

Answer 472

This is the relative ease for a metal to be melted. In general softer metals are more easy to fuse

Question 473

Volatility

Answer 473

This is the ease at which a substance is vaporized

Question 474

Is volatility and fusibility directly related?

Answer 474

They are not meaning that fusibility and volatility are dpendent on the specific material.