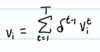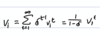Game Theory Flashcards
(36 cards)
Define what makes a rational agent.
Agent is rational if they choose a€A that maximises payoff
a*€A is only chosen is v(a*) > v(a) for all a€A
What are the methods of evaluating solution concepts?
1) Existence - is there an equ?
2) Uniqueness - is there >1?
3) Invariance - is it likely to change
What are static games?
Set of players make independent, once and for all decisions after which the outcome is realised
What is complete information?
Common knowledge available among all players off all actions, outcomes, each players preferences over outcomes and impact of actions on outcomes.
What is a strategy profile?
Descriptions of pure stratefies for all players
eg. (s1, s4, s2) for players 1,2,3
What is pure strategy?
A deterministic plan of action
Set of possible pure strategies for player i is given by Si
What is a normal form game?
Includes:
- Finite set of players
- Collection of pure strategies - {S1, S2, .., Sn}
- Set of payoff functions - {v1, v2,.., vn}
What is pareto optimality?
- A strategy profile s€S dominates s’€S if its payoffs are equal or higher for all players and at least one player’s payoff is higher.
- vi(s) >= vi(s’) for all i €N
What is a strictly dominated strategy?
A strategy is strictly dominated by another if, for any combination of the other players’ strategies, another strategy will have a higher payoff.
vi(si, s-i) > v(s’i, s-i)
What is weak dominance?
A strategy is weakly dominated by another if the payoff is equal or less than another strategy given any strategy of the opponent.
What is IESDS and explain the steps.
- IESDS = Iterated Elimination of Strictly Dominated Pure Strategies
- Identify strictly dominated strategies for all players
- remove these
- Treat whats left as a new game and repeat until there are no strictly dominated strategies
- Remaining strategic profile is the ‘iterated-elimination equilibrium’
How do you find the set of rationalizable strategies?
- Underline the best responses for each player in response to all others’ strategies
- If a row of P1 payoffs has no underlining, remove it
- If a column of P2 payoffs has no underlining, remove it
- Repeat to find BR
What did Keynes discover about IESDS in reality?
- 1938 Beauty Contest
- Two player choose number between 0 and 100
- closest to 2/3 of average wins - prediction would be 0 with IESDS
Reasons why players did not choose 0:
- Cognitive bias - Nagel (1938)
- Chou (2007) found if hints are given, better performance
- Camerer (2003) - Iterations involved complex thinking, limited working memory.
What is a Nash Equilibrium?
- Where each player is playing a best response to a belief and that belief is correct.
- NO incentive to change strategy
- vi(s*i, s*-i) >= v(s’i, s’-i) for all si€Si and all i€N
When do we get a unique Nash equilibrium?
When we have any of:
- Strict dominant equilibrium
- Sole survivor of IESDS
- Unique rationalizable strategy
What are the requirements for a Nash Equilibirum?
- Each player is playing a BR to their belief
- Beliefs about opponents are correct
What are some properties of Nash Equilibria?
- Stability - no incentive to deviate
- Self fulfilling - if there are multiple NE & players agree on one, they wont deviate
What are some limitations of Nash Equilibria?
- No guarantee of existence
- Insecurity about others actions
- Can be multiple NE and would need coordination to achieve one
What can happen when there are multiple Nash Equilibria (multiplicity)?
- If coordination is allowed we can get agreements even if they arent enforced
- Repition may lead to coordination
- A pareto dominant equilibrium may arise
What is the concept of the maxmin strategy?
Reduces uncertainty - Player is finding the best worst case scenario, so opponents actions are less likely to affect them negatively
How do you find a maxmin strategy?
- Find the minimum possible payoff for each strategy
- Play the strategy with the highest value of these minimums
What is a mixed strategy?
- Where a player plays a probability distribution over their strategies
- mixed strategy given by σi={ σi(si1), σi(si2), …, σi(sim) }
- eg for Rock paper scissors {R, P, S}, mixed strategy could look like σ = { 1/3, 2/3, 0}
What are the properties of a probability distribution in mixed strategies?
- all probabilities are above or equal to 0
- All probabilities sum to 1
What is an expected payoff in mixed strategies?
- Calculated expected payoff from a given strategy given the beliefs of your opponents strategies
- vi(si,σ-i) = Σ payoff x probability = Σvi(si,s-i)σ-i(s-i)