Game theory Flashcards
(16 cards)
Strategy
Complete set of actions for each player
Pure strategy
Strategy in which it is a player’s best response to take the same action regardless of others actions
Strategy profile
A strategy for every player in a game
Nash equilibrium
Set of strategies (one for each player) such that each player’s strategy is a best response to the strategies of other players Leads to equilibrium outcome Hence no-one wants to change their strategy
Bertrand
Price setting (think BP) -COnsumers buy from lowest priced firm -Will continue to undercut each other until MC
Cournout
Quantity setting -Takes other firms output as given -Calculate BR curve -Solve simultaneously for equilibrium
Stakleberg
Sequential quantity setting -Firm 1 moves first -It is given that firm to responds with (cournot) BR curve -Hence firm 1 optomises with this (choosing best point on BR curve)
Subgame perfect Nash equilibria
Must constitute a Nash equilibria in every sub game
Finitely repeated games
If a stage game with a unique NE is played a fixed and finite number of times then simply repeat same unique subgame perfect equilibria.
Discount rate
for an interest rate r
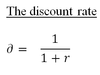
When will a firm stick to collusion
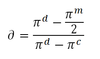
Minmax punishment
The worst that one player can do to another given the other is responding optimally - individually rational if guarentees minmax payoff
Minmax payoff
When a player responds optimally to another player punishing them.
Folk theorem
Any feasible payoff pair which gives each player at least her minmax payoff can be supported as a Nash equilibrium of an infinitely repeated game if the discount factor is sufficiently close to 1 (the players are sufficiently patient)
Friedman’s alteration to Folk Theorem
Friedman 1971
Any feasible payoff pair which gives each player at least her minmax payoff can be supported as a sub-game perfect Nash equilibrium of an infinitely repeated game if the discount factor is sufficiently close to 1 (the players are sufficiently patient)
How to plot mixed strategy nash equilibria diagrams
- Plot pure nash equilibria
- Plot mixed strategy
- Draw x through mixed strategy
- Join up corners


