Further Mechanics Questions Flashcards
(9 cards)
State and explain how the tension in the ropes of the trapeze varies as the acrobat swings on the trapeze. (3)
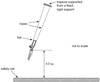
Tension minimum at extremities or maximum at middle / bottom
Tension depends on (component of) weight and required centripetal force / velocity
Increases as acrobat moves downwards
Tension at bottom = mg + mv2/r or Tension = weight + centripetal force
Tension at extremity = mg/cosθ (θ is angle between rope and vertical)
Explain why the period of the trapeze changes when the acrobat lets go of the bar.
(2)

Period shorter
Centre of mass of trapeze artist was lower than the bar
Effective length of the pendulum is lower
Bar likely to be low mass now have a pendulum with distributed mass / no longer a simple pendulum / centre of mass is half way along suspending rope
Calculates new effective length of the pendulum (2 m)
Explain why, when the student rises above point P, her motion is no longer simple harmonic. (2)
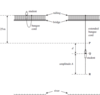
bungee cord becomes slack
student’s motion is under gravity (until she returns to P)
has constant downwards acceleration or acceleration is not ∝ displacement
The bungee cord has a significant mass. Whereabouts along the bungee cord is the stress a maximum? Explain your answer. (2)

at uppermost point or where it is attached to the railing
because stress = F/A and force at this point includes weight of whole cord
A lead ball of mass 0.25 kg is swung round on the end of a string so that the ball moves in a horizontal circle of radius 1.5 m. The ball travels at a constant speed of 8.6 m s–1.
Discuss the motion of the ball in terms of the forces that act on it. In your answer you should:
- explain how Newton’s three laws of motion apply to its motion in a circle
- explain why, in practice, the string will not be horizontal.
You may wish to draw a diagram to clarify your answer.
The quality of your written communication will be assessed in your answer. (6)
- First law: ball does not travel in a straight line, so a force must be acting on it
- although the ball has a constant speed its velocity is not constant because its direction changes constantly
- because its velocity is changing it is accelerating
- Second law: the force on the ball causes the ball to accelerate (or changes the momentum of it) in the direction of the force
- the acceleration (or change in momentum) is in the same direction as the force
- the force is centripetal: it acts towards the centre of the circle
- Third law: the ball must pull on the central point of support with a force that is equal and opposite to the force pulling on the ball from the centre
- the force acting on the point of support acts outwards
- Support of ball: the ball is supported because the rope is not horizontal
- there is equilibrium (or no resultant force) in the vertical direction
- the weight of the ball, mg, is supported by the vertical component of the tension, F cos θ, where θ is the angle between the rope and the vertical and F is the tension
- the horizontal component of the tension, F sin θ, provides the centripetal force m ω2 r
Are the oscillations of the pendulum more heavily damped when the cone oscillates with the metal ring on it, when it oscillates without the ring, or does the presence of the ring have no effect on the damping of the oscillations?
Explain your answer (3)
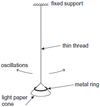
damping is caused by air resistance ✓
area is the same whether loaded or not loaded ✓
loaded cone has more kinetic energy or potential energy or
momentum (at same amplitude) ✓
smaller proportion (or fraction) of (condone less) energy removed
per oscillation from loaded cone (or vice versa) ✓
inertia of loaded cone is greater ✓
A rider of greater mass now uses the ride. Explain how the height of P has to be changed to produce the same initial amplitude of oscillations as that for the previous rider. (3)
it would have to raised
rest extension would be greater/rider would be
nearer the ground if extension unchanged
the rider has to move down a distance = to the
amplitude (5.9 m) from the new rest position
or with same initial extension/energy stored in rope,
the rider would reach a lower height
amplitude would be lower
or due to the larger mass more energy (= mgh) is
needed to reach the same height
so initial extension would have to be increased
A safety officer examines the design of the ride and thinks that, if the end P of the rope is raised too high so that the rope is stretched too much at the start, there is a risk that the rider could hit the ground after the first oscillation and suffer an injury.
Describe what would happen to the rider during the ride in this case and explain why, even if air resistance is negligible, the safety officer’s concerns are unfounded.
(3)
the rope would become slack at the top of the
ride so the rider would go into free flight/rider
would overshoot the highest point
the rider would fall and, with negligible air
resistance, the rope would again absorb the energy
arriving back at the start point or rider is more likely
to fail to reach the ground after one oscillation
due to energy losses/air resistanc
the PE gained (at the top of the flight) can (at most)
only be converted back to the elastic energy that was
stored in the rope at the start
(allow a statement to the effect that to hit the floor
would contravene conservation of energy or require an
energy input)
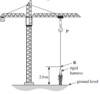
Discuss the consequences for the forces acting on the pole when one acrobat has a much greater mass than the other. (3)

Vertical (compressive) force on the pole increases ✔
Increases mass increases weight and hence tension in the rope(for the same angle) 1✔
Centripetal Force
on the acrobats/masses would be different/not equal
OR
Would be greater on the more massive acrobat(travelling at the same speed/same angle to vertical) 1✔
Unbalanced (horizontal) forces/resultant force exists (on the pole) ✔
OR
Unbalanced moments acting (on pole)/resultant torque acting (on pole) ✔
Causing the pole to sway/bend/move/ or tilt/topple the platform toward more massive acrobat 1✔


