Further Mechanics Flashcards
Momentum is always (………..)
Conserved
What does the Linear momentum of an object depend upon?
Mass & Velocity
Is momentum a Scalar or a Vector?
Vector
What is the Momentum equation?
p = mv p - Momentum (kg m s*-1) m - Mass (kg) v - Velocity (ms*-1)
What do we assume is true if momentum is conserved?
There is no external forces acting on the object
Does momentum apply for explosions?
YES
How do you resolve Linear Momentum?
Split it into its Horizontal and Vertical Components
What are the Laws of Momentum?
Momentum before a collision = Momentum after a collision
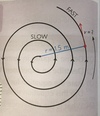
How do you investigate momentum in 2D?
- Weigh two ball bearings and note down their masses - On the table, position two metre rules at right angles to each other, put one of the ball bearings on the table and position a video camera directly above the table so it has a birds eye view. Like the picture! - Start videoing, roll the second ball bearings towards the stationary ball bearings so they collide - Use video analysis software to study the collision - Find the time between each frame and calculate how many frames are in each 0.1s - Use the rulers to find the distance travelled horizontally and vertically of the ball bearings every 0.1s, - use trigonometry to find the magnitude of the balls Velocity before and after the collision - Use Trigonometry to find the directions of these velocities. - You can find momentum is conserved by calculating the total momentum before the collision and the total momentum after the collision
What is an Impulse?
Is the change in momentum
What does Newton’s 2nd Law say?
Force = rate of change of momentum
What are the units of an Impulse?
Ns
The area under a force-time graph is…
Impulse
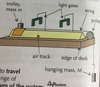
How do you investigate an Impulse (F X Δt = Δp) with an air track and Light Gates?
- Set up the apparatus and connect the lights to a data logger and computer - Release the trolley at one end of the air track and the weight will pull it along - Total mass of the system equals mass of the trolley + hanging mass - Use the data logger to find the Velocity of the trolley at each light gate. - Use this information to calculate the impulse (Δp *system* = m *system* X Δv) - Can also use the data logger to find the time taken for the trolley to travel between the two light gates, use this to find the rate of change of momentum in the system, Δp *system* / Δt - Repeat and take an average value for the impulse - Force acting on the system = Weight of hanging masses, F = Mg - Repeat the experiment with varying masses, every time you change the mass of the hanging mass add it to the trolley to keep the total mass of the system the same - Plot of graph of Force against rate of change of momentum - The graph should be a straight line.
Kinetic Energy is the energy of…
Anything moving
What does Kinetic Energy depend upon?
Mass & Velocity of whatever is moving
What are the 2 Kinetic Energy Equation we MUST know?
KE = 0.5 X m X v*2
KE = p*2 / 2m
V - Velocity of the object
M - mass of the object
P - momentum
How do you derive the equation KE = p*2 / 2m ?
Use KE = 0.5 X m X v*2
And
p = mv
Substitute p in for mv
KE = pv / 2
Rearrange p = mv to give v = p/m and substitute KE = pv / 2
TO GIVE
KE = p*2 / 2m
In what kind of Collision is Kinetic Energy Conserved?
In Elastic Collisions
If after a collision the object stick together or bounce apart is momentum still conserved?
YES
A collision where the total kinetic energy is the same after a collision is called…
An Elastic Collision
A collision where the total kinetic energy is less after a collision is called…
An Inelastic Collision
In a Collision is Energy conserved?
Yes, conservation of energy applies!
In a collision what is meant when it is said that energy is ‘lost’?
It means it is transferred to other forms of energy.
How can Angular Displacement be expressed?
In Radians or Degrees
What is Angular Displacement?
Is the angle through which a point has been rotated in a given direction.
How is the Magnitude if Angular displacement expressed?
In radians
How do you calculate the Angular displacement?
Arc - Length / radius of the circle
How many radians are in a complete circle?
2π rad
What in radians is a 45 degree angle change?
π / 4 rad
What in radians is a 90 degree angle change?
π / 2
What in Radians is a 180 degree angle change?
π
How do you convert from degrees to radians?
Multiply by π / 180
How do you convert from radians to degrees?
Multiply by 180 / π
What is the value of 1 Radian?
57 degrees
Define Angular Velocity.
Is defined as Angular displacement over time
What are the units for Angular Displacement?
Rad s*-1 (radians per second)
What is the the Angular Velocity Equation?
ω = θ / t
ω - Angular Velocity (rad s*-1)
θ - is the angle in rad turned in a time
t - Time (s)
What is the Linear speed equation?
v = ωr
v - Linear speed (ms*-1)
ω - magnitude of the Angular Velocity (rad s*-1)
r - radius of the circle (m)
What is the difference between these two equations? v = ωr & ω = θ / t
The ω on the Equation ω = θ / t is the ANGULAR VELOCITY you can then substitute this value into this equation v = ωr
What is another name for Linear speed?
Tangential speed
Explain why the Linear speed of the particles increases as they spiral outwards, even though the angular speed is constant.
Linear speed, depends upon the radius of the circle. So as r increases so does v even though ω remains constant.
Circular motion has a…
Frequency and Period
Define Frequency.
Is the number of complete revolutions per second
What is frequency measured in?
Hz (Hertz)
Define a Period.
Is the time taken for a complete revolution (in seconds)
Show the equation that links Period and Frequency.
f = 1 / T
What’s a complete circle in radians?
2π
What is the equation that links Angular speed to Frequency?
ω = 2πf
ω - Angular Speed (rad s*-1)
f - Frequency (Hz)
What is the equation that links Angular speed (ω) and Time Period?
T = 2π / ω
Are objects in a Circle accelerating even if their speed doesn’t change? Why?
YES! This is because their direction is constantly changing.
Derive the equations (a = v*2 / r) and (a = r X ω*2). Really LONG! Circular Motion
1 - Imagine a ball moving in a circle, and you take an arc of the distance it moved.
2 - Resolve point A and point B into Horizontal and Vertical Components. (Diagram i drew)
The reason why it is minus v X sin θ is because it is in the other direction. We call the time it takes to get from point A to Point B, T.
3 - Angle between -v X sinθ and B is equal to half the arc θ.
4 - In the Vertical direction a = v - u / t
So :
(V X cosθ - V X cosθ) / t = 0
Because it equals 0 we can ignore the Vertical Direction
5 - Look at the Horizontal Components.
a = v - u / t
So :
(V x sinθ - - V X sinθ) / t
Simplify :
a = 2 v sinθ / t
6 - We know the Angular Velocity = θ / t
v = ω / r
Substitute these together - v = θr / t rearrange for t - t = θr / v
7 - Because the object rotates through 2π Change Equation too…
t = 2θr / v
8 - Substitute t = 2θr / v into a = 2 v sinθ / t
a = (2vsinθ) / (2θr) / v
a = v*2 sinθ / θr
You can cancel out the sin.
9 - a = v*2 θ / θr
Simplify - a = v*2 θ / θr
You get - a = v*2 / r
10 - v = ωr
a = v*2 / r = ω*2 r*2 / r
a = ω*2 r
What is Centripetal Acceleration produced by?
Centripetal Force
If there is Centripetal Acceleration in which direction does the force act?
Towards the centre
What would happen if you removed the Centripetal Force of an object moving in a circle?
The object would fly off at a tangent
What are the Centripetal Force equations?
F = mv*2 / r
&
F = mrω*2
