Fundamentals of Magnetic Resonance Flashcards
Define nuclear spin, give its units and describe what values it takes in different nuclei.
Nuclear spin, I, is the total angular momentum of a nucleus. It is measured in units of ħ which is h/2π.
The nuclear spin can be an integer or an half-integer.
If the no. of protons and neutrons are even, spin is 0
If the no. of protons and neutrons are odd, spin is and integer
If one is odd and the other is even, the spin is a half-integer
How can the number of spin states for a nuclei be determined from the nuclei spin? How does this relate to the eigenvalue of the vector of the spin in the z direction?
Using m = 2I + 1 the number spin states can be determined. For 1/2, the states are -1/2 and 1/2.
The eigenvalues of Iz operator are mħ where m is the values determined above.
How does the nuclear spin affect the nuclear magnetic moment?
The nuclear magnetic moment, μ^, is given by γI^.
Where γ is the gyromagnetic ratio which is a property of the nucleus where γ/2π has the units of MHz T-1. γ is usually given in this form.
Describe the Zeeman interaction and how it can be described by a Hamiltonian. How can this be applied to the energy of the nuclei’s spin states?
The Zeeman interaction is the force when a nuclei is placed in a large magnetic field. The Hamiltonian is H^z = -μ^z • B0 = -γ I^z B0 where B0 is the magnetic field in the applied direction (defined as z).
Recalling that the eigenvalues are mħ, the energy of each spin state is:
Em = -γ B0 m ħ for various values of m.
Hence the difference between adjacent spin states is γ B0 ħ. And as the selection rule is ±1, this is always the energy gap.
How does the difference in energy between spin states relate to the frequency of the radiation to cause a transition between the states?
ω = γ B0 also know as the Larmor equation
ω = 2πv where v is the Larmor frequency.
Typical Larmor frequency values are 102 MHz
How are the number of nuclei in each state determined?
Via a Boltzmann distribution probability. At thermal equlibrium both states are very similar in population as they are close in energy. The difference in population at equlibrium is known as the nuclear polarisation, P. This depends on the field, B0, the gyromagnetic ratio and the temperature. This has a high temperature approximation.
Describe the coordinate system often used in NMR.
Describe how the magnetic moment is divided into these componants
Cylindical coordinates where z is the B0 axis, ρ is the distance in the xy plane from the origin and φ is the angle of the vector in the xy plane.
μz = μz, μx = μxycosφ, μy = μxysinφ
What is generated as a product of the magnetic field and the magnetic moment of a nuclei?
A torque which acts perpendicularly to both vectors. This causes the nuclei to precess about the magnetic field vector, at the Larmor frequency, ω = γ𝐵0.
Describe the nuclear spins in a sample and how they are oriented before and after a magnetic field is applied. Describe the net magnetisation.
Without a magnetic field, the nuclei point in any direction as none are preferred. Once the field is applied, the Zeeman interaction creates a preference for spin up nuclei and they will all precess about the B0 direction.
The sum of the magnetic moments is the net magnetisation, M. Mz is the sum of all z components of the magnetic moments. Mxy is the sum of the xy componants which depends on the phase of precession.
What determines the total magnetisatiation along the z axis?
The total magnetisation along z = P0 (the polarisation at equlibrium, asigns the difference in spin state population) • N (number of spins in the sample) • size of the magnetic moment (mγħ)
This therefore depends on the number of spins, the type of nucleus, B0 and temperature.
Describe the traverse magnetisation of the nuclei, Mxy.
As the nuclei precess, the phase will depend on time and the initial phase. This can be represented as a function of the two directions and converted to a more useful form using Eulers formula.
The phase of the nuclei at time t only depend on the phase when they were pointing at time t=0. At equlibrium these phases are random and on average they will cancel out for entropic reasons. Hence Mxy = 0.
There can only be magnetisation in the xy plane if there is initial phase coherence.
Describe the product of rotating the total magnetisation at equlibrium into the xy plane in terms of signal, phase coherence and polarisation.
As the magnetic moment is in sync, there is phase coherence. This means that when a coil is placed around the field, the precessing magnetic moment will generate an oscillating current. As there is no magnetisation along the z axis, there must be an equal population in both spin states. The rotation will be at the Larmor frequency.
Describe the basis of the rotating frame of reference.
To represent the precessing transverse vector, new axis of z’, x’ and y’ are used where x’ and y’ are rotating at the Larmor frequency. Since the vector is stationary in the rotating frame of reference, the field vector, B0, will dissapear.
Describe, using the rotating frame of reference, the RF pulse that induces transitions between energy states. Describe the RF pulse amplitude, frequency and duration and what effect this has on the magnetisation vector.
The RF pulse must have a magnetic field that rotates at the Larmor frequency (energy to move nuclei between states). This relates to a frequency in the radio range. The amplitude, B1, is in the mT range, smaller than B0. The duration is given by tRF.
In the rotating frame, the magnetisation vector will rotate perpendicular to the RF pulse. The pulse is applied perpendicular to the field so the vector will rotate in the plane of z and either x or y (depending on the RF pulse direction). The rotation will occur with the frequency ω1 = γB1.
When an RF pulse is applied to a vector, what determines the angle it is rotated to?
The angle, α = ω1tRF = γB1tRF.
Any angle from the z axis can be rotated to, it only depends on the time the RF pulse is applied for.
Describe the uses and effects of longitudinal (T1) relaxation.
It can be used as a information source about the structure and dynamics of the system, such as MRI.
The rate of change of the z magnetisation = -T1-1 [Mz(t) - M0]. The relaxation rate, R1, is the reciprocal of the relaxation time. T1 is a function of the physical characteristics of the sample, such as temperature and viscosity.
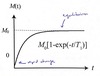
The main role of T1 is the time used to determine how long between RF pulses so that enough of the sample has relaxed. This is described by the equation Meff = M0 (1 - exp(-TR/T1) where TR is the time between RF pulses. If 2T1 is waited, 86% of the sample will have relaxed. Enough time must be left so that integrals are accurate, for full accuracy, 5T1 are left.
Describe the transverse (T2) relaxation rate dependancy and the effect this has on the NMR signal.
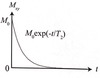
The rate of change of Mxy only depends on T2, a property of the sample. Therefore Mxy = M0exp(-t/T2). The Mxy moment causes the signal and T2 causes its decay.
In some cases Mxy will also decay due to reversible dephasing which along with local field differences and the differences in the sample will give rise to an effective relaxation time, T2*. This can then be compared with the fundamental T2 to find the field imhomogeneity.
A long T2* (close to T2) is optimal and gives rise to long signals/narrow peaks. Shimming is used to improve B0 homogeneity by applying small additional fields to remove variations.
Summarise the longitudinal and transverse magnetisation with graphs for when B0 is initially applied, when a 90º RF pulse is applied and when the signal is detected.
