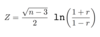Brainscape's Knowledge GenomeTM


Top Flashcards (Certified)
All Flashcards

Business Statistics Year 2 > Formulas and Definitions > Flashcards

Formulas and Definitions Flashcards

(56 cards)

Start Studying
1
Q

Q1=

A

0.25 (n+1)th value

OR

(n+1)/4

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

Q2=

A

it’s the median

(n+1)/2

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

Q3=

A

0.75 (n+1)th value

OR

3(n+1)/4

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

Ecart entre 2 quartiles =

A

Interquartile range

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

Median =

A

To find the Median, place the numbers in value order and find the middle.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

Variance =

A

𝞼2

Average of squared differences from the mean

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

Why using samples?

A

We rarely can collect data on ALL members of a population because of Time and Cost, but we still need to be able to make conclusions about the entire population.

So we use samples

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q

Samples guidelines and bias:

A
  • All elements in the sample must be part of the population as it’s defined
    • Bias: people under/over the age boundary
  • The sample should be representative of the population
    • Bias: collecting data on height and half of the sample plays in the NBA
  • Samples should be independent from each others
    • Bias: “Refer a friend” to the study as friends often have a lot of similarities
  • Samples are chosen randomly in many cases
    • Bias: Only choosing people from a particular background/ethnicity when the study is about a multicultural country

Sample results are ALWAYS an approximation

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

Measure of Skewness

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

Standard deviation =

A

Square root of variance

𝞼

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

When should we prefer the mean or the median ?

A

The mean is mostly preferred because it uses all the data values

However, in case of extreme values, the median might be more representative

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

Measures of spread VS measures of location

A
  • Sample mean and median are measures of location. They give you a ‘typical’ value of an observation.
  • Sample variance and inter-quartile range are measures of spread. They tell you how far observations tend to be from the ‘typical’ value.
  • The largest and smallest values give the range of the data, but this is not usually a robust measure of the range of values in the population (as it can vary alot among independent samples).
  • The set of five values (x(1), Q1, Q2, Q3, x(n)) is called the five point summary.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

Bar chart

VS

Histogram

VS

Box-and-whisker plot

A

Bar chart: For discrete data. Vertical bars are separate; height is proportional to frequency.

Histogram: For continuous data. Vertical bars are adjacent; if interval widths are different, the area of the rectangle is proportional to frequency.

Box-and-whisker plot: Produced with median, quartiles, max and min. The box extends from one quartile to the other, with the median marked in between.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

Symmetry:

A

Sometimes it is important to judge whether a dataset is symmetric. Look at :

  • Whether mean and median are close
  • Whether median is about midway between the quartiles
  • Whether the histogram is symmetric
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q

Different statistical models:

A
  • Yes/No survey (binomial)
  • Number of computer server crashes at City University per week (Poisson)
  • Returns on shares (normal)
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

Standard Normal curve

A

A commonly used distribution for continuous variables is the Normal distribution illustrated below. It is symmetric. Parameters are μ, the mean, and σ the standard deviation.

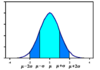
The curve in the image has a sdev of 1

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
17
Q

Normal tables:

A

Z is said to have a standard normal distribution.

To calculate probabilities associated with Normal variables, use tables or computers. Normal tables usually give Φ(z) = P(Z ≤ z) only for positive numbers z. Equivalent values for negative numbers z can be found by symmetry:

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
18
Q

Characteristics of a Binomial Experiment:

A
  1. The process consists of a sequence of n trials
  2. Only two exclusive outcomes: success or failure
  3. Probability of success = p
  4. Probability of failure = 1-p
  5. Trials and outcomes are independent
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
19
Q

Binomial notations

A

X∼Binom(n,p)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
20
Q

Binomial success probability formula

A

n=total population

j= success

p= probability

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
21
Q

Binomial coefficient calculation formula:

A

(x! on calculator)

Use nCr in calculator

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
22
Q

Normal approximation to Binomial:

A

When n is large, Binomial(n, p) gives roughly the same results as N (np, np(1 − p))

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
23
Q

Continuity correction: for X Binomial and Y Normal:

Study These Flashcards
A
  • P(X > 10) = P(X ≥ 11), but
  • P(Y > 10) ≠ P(Y ≥ 11),
so we use P (Y \> 10.5) as a suitable approximation.
Similarly P(X \< 10) = P(X ≤ 9) so use P(Y \< 9.5) as an approximation.
24
Q

Random variable, Distribution and Observations:

Study These Flashcards
A
  • A random variable is a numerical quantity whose value is to be determined by an experiment, but the experiment has not yet been performed.

Examples are: score on a die, height of a random student.

  • A distribution describes the values that might be observed and how likely they are. Many quantities can be assumed to have standard distributions, like Normal, Binomial.
  • After the experiment the value is known: this is an observation.

We use X, Y, Z to denote random variables, x, y, z to denote observations.

25
Confidence interval
95% confidence interval for μ
26
df=
Degree of freedom = sample size minus 1 = **n-1**
27
If If σ is unknown for a confidence interval...
We can use S as an estimate of σ. But the distribution now changes: it is not Normal but Student’s t: The shape of the t distribution depends on the *degrees of freedom*: this is *n − 1* in this case. It is symmetrical about the origin.
28
Confidence interval for proportions: Normal approximation for Binomial
Example: in a sample of 100 people, 55 said they were opposed to the Euro. Find a CI for the population proportion. If X is the number of people in a sample of size n who agree with a given statement, then for large n so that: X ∼Bin(n,p) ≈ N(np,np(1−p)) * **p is unknown so the best estimator is X/n** * **The df is "infinity"** then
29
Null Hypothesis =
**H0**= Null hypothesis = opposite of statement made **H1** = Alternative hypothesis = assumption being tested
30
The F Test is for... The t-test is for...
**F:** Testing whether two independent normal samples come from populations with the same **variance**. **t:** Testing whether two independent normal samples come from populations with the same **mean** The results found with the formulas should be compared to those found in the t or F tables. tcrit lower limit is found by adding "-" in front of the number in the table
31
Use of the F Test:
* The **2-sample** **t test** **can only be performed if σ12 = σ22**. The F test is often used to see whether it is permissible to use the 2-sample t test. (**Place the larger variance on top**) * It has many other uses as well: see **ANOVA**, **Linear Regression**.
32
When to use *z* or *t* distributions?
**t-distribution special characteristics:** * Sample size **n≤30** and/or * We don't know the variance/standard deviation
33
Poisson distribution definition
Poisson distribution focuses on the number of discrete events or occurences over a specified interval or continuum (time, length, distance...)
34
Poisson distribution formula (ne pas apprendre?)
35
Chi-square test formula:
Use the chi table to compare the results. **df**= Number of categories - Number of restrictions **Number of restrictions =** 1 + Number of estimated parameters **For Binomial, df=** number of observation in one group - 1
36
Why using ANOVA? ANOVA Null Hypothesis:
* To compare the means of more than 2 populations * To compare populations each containing several levels/subgroups H0: μ1 = μ2 = µ3
37
(One-way ANOVA) Treatment? Error? Sum of Squares?
**Treatment** = Between = Distance of each mean from overall mean **Error** = Within = Internal spread/standard deviation of each sample distribution **Sum of Squares** = Sum of all squared distances from the means (SSE) **/** overall mean (SSTr)
38
MSTr=
Mean Square Treatment SSTr/dftreatment
39
MSE=
Mean Square Error MSE = SSE/dferror
40
The p value:
**p value \< 0.05** : **reject** null hypothesis **p value \> 0.05** : **don’t reject** it, (but can say “There is some evidence against H0” if 0.05 \< p \< 0.10)
41
Assumptions for ANOVA:
* Each sample comes from a population that follows a normal distribution * Equal Variances * All sample are independent and randomly selected
42
Why two-way ANOVA?
The variations from the mean were attributed to the colums or the error with one-way ANOVA. With two-way ANOVA we want to know which proportion of the error's variations can be attributed to the row variations. We want SSE to be as small as possible as we compare it to the SSC for the F-ratio
43
fitted value=
**row mean + column mean - grand mean**
44
residuals=
**actual value - fitted value**
45
Two-way ANOVA SSE =
**sum** **of squared residuals**
46
R2 = Coefficient of determination =
* **SSR / SST** * **SSTr / SST** Interpretation: * **R2 = 0** ⇒ The dependent variable **cannot** be predicted using the independent one * **R2 = 1** ⇒The dependent variable **can** be predicted using the independent one * **0 \<** **R2 \< 1** ⇒ A coefficient of determination that falls within this range measures the extent that the dependent variable is predicted by the independent variable. An R-squared of 0.20, for example, means that 20% of the dependent variable is predicted by the independent variable A coefficient greater than 0.85 is a GOOD FIT
47
"Interactions two way ANOVA:
An interaction means that the main effects can not be relied upon to tell the full story. When there is an interaction effect, it means the main effects do not collectively explain all of the influence of the IndependentVariables on the DependantVariable. The IVs have an interactive effect on the DV, which means the cell means must be examined for each sub-group -- this is where the nature / direction of the interaction can be found.
48
H0 for linear regression
**H0= *y* does not depend on *x***
49
Residuals:
* Distance between "raw best-fit line" (mean of dependant variable) and the observed value. Also called **Error**. SSE= Sum of Squared Errors Raw SSE = SST * After conducting a regression, the SSE should be greatly diminished (becomes distance between the calculated best-fit line and the observed values). The difference SST - newSSE = SSR (regression)
50
Scatter plot=
Coordinate plan, un repère. The dependent variable is on the left
51
Slope intercept form of a line:
***y = α + ßx*** * x = random variable * ß = slope of the line (rise over run) * α = y-intercept (cross y-axis)
52
Correlation =
* r is always between -1 and 1 * Values close to **1** show a strong **positive linear relationship**; * Values close to **-1** show a strong **negative linear relationship**; * Values close to **0** indicate **no linear relationship**.
53
Fisher’s Z:
* Z is roughly N(0,1) if H0 is true. So **we reject H0 if the observed value of Z is \> 1.96 or \< −1.96.**
54
p-value
**(1 - p(z)) \* 2**
55
Adjusted R-squared:
Notice that the denominator, SST/(n−1), can alternatively be called MST.
56
Multicollinearity=
The Independent values are potentially related to each other. There is a relationship among them. Ideally, we don't' want IV to be correlated with each other. When they are, we don't want to use them both in the multiple regression, they are redundant. It can be tested using scatterplots and correlation

Business Statistics Year 2 (2 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2025 Bold Learning Solutions. Terms and Conditions