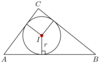Formulae Flashcards
Formulae and theorems important for AMC 10
Area of a triangle with sides a, b and included angle θ
1/2 · a · b · sin θ
a, b, c are the sides of the triangle with circumradius R.
abc/4R
Proof
Area of a kite
2.2 cm wide and 8 cm long
- d1</sub>d2
8. 8 cm2
Area of cyclic quadrilateral
- s = (a + b + c)/2
- sqrt( (s-a) * (s-b) * (s-c))
where s is the semiperimeter and a, b and c are the side lengths.
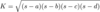
Area of triangle with sides a, b and c
- Let s= (a + b + c)/2
- Area = sqrt (s * (s-a) * (s-b) * (s-c))
Heron’s formula:
Area of regular polygon with perimeter p and apothem a.
- pa/2*
- p·cot 180/n* (where n is the number of sides)
- Inscribe the polygon a circle
- Draw a line from two adjacent vertices to the circumcenter.
- This creates a triangle that is 1/n of the total area.
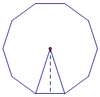
Apothem: length of
The apothem of a regular polygon is the line segment drawn from the center of the polygon perpendicular to one of its edges. It is also the radius of the inscribed circle of the polygon.
Given the number of sides n and side length s the length of the apothem is s /( 2·tan (π/n) ).
Area of a regular hexagon with side s
A = (3/2)* sqrt(3) * s2
area of a hexagon with perimeter 24 cm
24*sqrt(3) square cm
~ 41.569 cm sq
Volume/Surface Area of a Cone
- V =πr2h/3*
- SA=πr2+πrl*
Where V is the volume, SA is the surface area, r is the radius of the circular base, h is the height, and l is the slant height.
Volume/Surface Area of a Sphere*
- V = (4/3 ) · πr3*
- SA = 4πr2*
Where V is the volume, SA is the surface area, and r is the radius of the sphere (which is radius of the central cross section/the base of the semisphere).
Volume/Surface Area of a Pyramid
- V = (1/2)bh*
- SA = 2sl + b*
Where V is the volume, SA is the surface area, b is the area of the base, h is the height, l is the slant height, and s is the length of a side of the base. Note that a pyramid can have a base of any polygon, but if none is specified, assume a square base. A pyramid with a triangular base is known as a tetrahedron.
Volume/Surface Area of a Prism*
- V =lwh*
- SA=2(lw+lh+wh)*
Where V is the volume, SA is the surface area, l is the length, w is the width, and h is the height.
Common Pythagorean triples
3 4 5
5 12 13
7 24 25
8 15 17
Important:or these side lengths multiplied by some factor, it is a right triangle)
distance between the line ax+by+c=0 and point (x1,y1) is
- |ax1 + by1+c| /sqrt(a2+b2)*
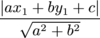
Distance between two points (x1,y1) and (x2, y2)
In the -dimensional case, the distance between (a1, a2 ..an) and (b1,b2, ..bn) is:
sqrt( Σ (ai-bi)2)
A convex quadrilateral is cyclic if and only if the four perpendicular bisectors to the sides are
Concurrent.
This common point is the circumcenter.
Angles of a cyclic quadrilateral ABCD with diagonals
∠A + ∠C = 180°
∠ABD = ∠ACD
∠BCA = ∠BDA
∠BAC = ∠BDC
∠CAD = ∠CBD
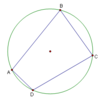
Ptolemy’s Theorem*
ab + cd = ef
Where ABCD is a cyclic quadrilateral with side lengths a, b, c, d and diagonals e, f (with a opposite b and c opposite d).
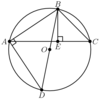
In ΔABC we have AB=7, AC=8, BC=9. Point D is on the circumscribed circle of the Δ so that AD bisects angle BAC.
What is the value of: AD/CD?
Set BD’s length as x.
CD’s length must also be x since ∠BAD and ∠ DAC intercept arcs of equal length(because ∠ BAD= ∠ DAC).
Using Ptolemy’s Theorem, 7x+8x=9.
The ratio is 5/3
◌
Brahmagupta’s Formula
K =sqrt ( (s-a)(s -b)(s-c)(s-d) )
Where K is the area and s is the semiperimeter of the quadrilateral with sides a, b, c, d. For this formula to work, the quadrilateral must be cyclic.
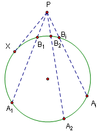
A hexagon is inscribed in a circle. Five of the sides have length 81 and the sixth, denoted by AB, has length 31.
Find the sum of the lengths of the three diagonals that can be drawn from A.
1991 AIME Problems/Problem 14
384
Let x=AC=BF, y=AD=BE, and z=AE=BD.
Ptolemy’s Theorem on ABCD gives 81y+31·81=xz and Ptolemy on ACDF gives x·z + 812 = y2.
Subtracting these equations give
y2-81y-112·81 = 0 ,
and from this y=144.
Ptolemy on ADEF gives 81y+ 812= z2 , and from this z=135.
Finally, plugging back into the first equation gives x=105,
so
x+y+z = 105 + 144 + 135 = 384.
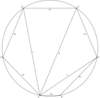
A quadrilateral is inscribed in a circle of radius 200*sqrt(2). Three of the sides of this quadrilateral have length 200. What is the length of the fourth side?
- Use Ptolemy’s
- Divide all side lengths by 200 to make computation easiers
- Construct quadrilateral ABCD on the circle with AD being the missing side (Notice that since the side length is less than the radius, it will be very small on the top of the circle). Now, draw the radii from center O to A, B, C and D. Let the intersection of BD and OC be point E. Notice that BD and OC are perpendicular because BCDO is a kite.
- set lengths BE=ED equal to x
- Solve for x using Pythagoras
- x=sqrt(14)/2
- By Ptolemy’s Theorem,
- AB*CD+BC*AD = AC*BD=BD*BD=(2*BE)2*
8. AD=5/2
9. Multiply by 200 ==> 500
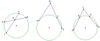
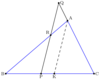
What are the 3 cases of the Power of a Point theorem?
The two lines are secants of the circle and intersect inside the circle (figure on the left). In this case, we have AE*CE=BE*DE
One of the lines is tangent to the circle while the other is a secant (middle figure). In this case, we have AB2=BC*BD
Both lines are secants of the circle and intersect outside of it (figure on the right). In this case, we have CB*CA=CD*CE
Power of Point Theorem: Compact formulation
Consider a circle O and a point P which is not on the circle.
Draw a line through P that intersects the circle in two places.
The product of the length from P to the first point of intersection and the length from P to the second point of intersection is constant for any choice of a line through P that intersects the circle.
This constant is called the power of point P.
For example, in the figure below
Chords AB and CD of a given circle are perpendicular to each other and intersect at a right angle. Given that BE=16, DE=4 and AD=5 find CE.
- ADE is a right triangle with hypotenuse 5 and leg 4.
- Therefore AE=3.
- Applying t Power of a Point Theorem gives AE*BE=CE*DE or 3*16=x*4
=> x = 12
Ceva’s theorem
Criterion for the concurrence of cevians in a triangle.
- Let ABC be a triangle
- Llet D, E, F be points on lines BC, CA, AB respectively. Lines AD, BE, CFare concurrent if and only if:
BD/DC · CE/EA · AF/FB = 1
where lengths are directed. This also works for the reciprocal of each of the ratios, as the reciprocal of 1 is 1.
Ceva’s theorem: idea behind proof
- Assume that the cevians are concurrent
- Show the Ceva property follows using ratios of areas of triangles.
- Concoct up a point F’ and show that F’ is the same as F.
Suppose AD, BE, CF meet at a point X.
Triangles ABD, ADC have the same altitude to line BC, but bases BD and DC.
It follows that BD/DC = [ABD]/[ADC] . The same is true for triangles XBD, XDC
Suppose D, E and F satisfy Ceva’s criterion, and suppose AD, BE intersect at X. Suppose the line CX intersects line AB at F’. We have proven that F’ must satisfy Ceva’s criterion.
=> AF’/F’B = AF/FB’ so
=> F’=F ,
=> CF concurs with AD and BE.
Menelaus’ Theorem
IFF P, Q, R on the respective sides BC, CA, AB (or their extensions) of a triangle ABC are collinear:
BP * CQ * AR = -PC * QA * RB
where all segments in the formula are directed segments.
Menelaus’ Theorem: idea behind proof
Draw a line parallel to QP through A to intersect BC at K:
An angle formed by three points on the circumference of the circle is equal to _ the measure of the subtended arc.
1/2
sin 2θ
2 sin θ cos θ
sin (α ± β)
sin α cos β ± sin β cos α
Sum of interior angles in a polygon
(n-2)<span><strong>·</strong></span>180°
Area of a polygon of inradius r and perimeter p
s*r
where s is the semi-perimeter
- Add incircle, drop altitudes from the incenter I.
- Draw the lines AI, BC and CI to make three sub-triangles AIB, AIC, BIC
- AB, AC and BC are the bases of these triangles with the same height r.
- => [ABC] = ar/2 + br/2 + cr/2 = sr where s is the semiperimeter
The sum of the exterior angles in a polygon:
360o
