First 8 Weeks Flashcards
Projection Formula of b onto a
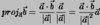
Component of V onto U
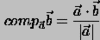
Dot Product

What is the Cross Product? in 2-space and 3-space?
- The cross product in 3D is the line that’s orthogonal to 2 vectors and can be calulated by a × b = |a| |b| sin(θ) n or in the determinant form below
- The absolute value of the cross product is the volume of a parallelepiped in 3D
- The absolute value of the determinant of 2 vectors in 2D is the area of a parallelogram it is equal to the cross product of 2 vectors, but the cross product isn’t defined in 2d.

Orthogonality - What’s point normal form?
The normal of the plane is the vector that’s orthogonal to the plane (a,b,c) and vector (a,b) for a line.

Distance between a point and a line or a plane
Distance can be found by computing the rejection if given in parametric form or by the formula if given by a point-normal form

The equation of a line that passes through x(0) and parallel to V
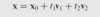
Equation of a plane that is parallel to V1 and V2
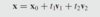
What’s the geometric representation of the cross product?
A = (base)(altitude) = |u||v| sin θ =
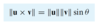
When 3 vectors are on one plane?
When they all have an mutual initial point and the formula below is true

The area of a parallelepiped
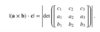
the area of the parallelogram spanned by a=a1i+a2ja=a1i+a2j and b=b1i+b2jb=b1i+b2j is
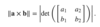
How to find the equation of the plane that passes through 3 points?
- Find the vectors between the points that sit on the plane. (a1-a0)…
- Find the cross product between 2 vectors
- The cross product will be the and pick any point for the (x-x1)(y-y1)…
What things do I need to describe a plane in a scalar equation?
- A vector that lies in the plane
- Normal vector to that vector from the plane
How to write a linear combination from V1 & V2 to fit A or B
- Take both vectors and ecuate to the new combination vecotor
- Solve in a matrix to see if there are any number C1 or C2 that will give us the solutions.
How to know if a linear combination spans {V1,V2}?
If it’s consistent and has solutions
- Find a vector equation and parametric equations of the line in R2 that passes through the origin and is parallel to the vector v = (−2, 3).
- Find a vector equation and parametric equations of the line in R3 that passes through the point P0(1, 2,−3) and is parallel to the vector v = (4,−5, 1).
In 2D: Vector form: (x,y)=(0,0)+t(-2,3)
Parametric form: x=-2t, y=3t
In 3D: Vector form: (x,y,z)=(1,2,-3)+t(4,-5,1)
Parametric form: x=1+4t, y=2-5t, z=-3+t
What 2 forms of vector equations we have to represent a 2-point vector line?
- x=x0+t(x1-x0)
- x=(1-t)x0+tx1


