First Flashcards
(15 cards)
Stochastic Process
Any variable whose value changes over time in an uncertain way.
Classification of stochastic process based on time
- Discrete time stochastic process
- Continueous time stochastic process
Classification of stochastic process based on variables
- Discrete variable stochastic process
- Continueous variable stochastic process
Markov Procss
A particular type of stochastic process where only the current value of a variable is relevant for predicting the future. The past history of the variable and the way that the present has emerged from the past are irrelevant.
Stock prices are usually assumed to follow a Markov process.
Markov Property
Implies that the probability distribution of the price at any particular future time is not dependent on the particular path followed by the price in the past.
Markov Property is consistent with ______ form of market efficiency because ___
Weak form of market efficiency
Competition in the marketplace that tends to ensure that weak-form market
efficiency holds.
If the weak form of market efficiency were not true, technical analysts could make above-average returns by interpreting charts of the past history of stock prices. There is very little evidence that they are in fact able to do this.
Consider a variable that follows a Markov stochastic process. Suppose that its current value is 10 and that the change in its value during a year is ø(0,1), where ø(m,v) denotes a probability distribution that is normally distributed with mean m and
variance v. What is the probability distribution of the change in the value of the
variable during 2 years?
The change in 2 years is the sum of two normal distributions, each of which has a mean of zero and variance of 1.0. Because the variable is Markov, the two probability distributions are independent. When we add two independent normal distributions, the result is a normal distribution where the mean is the sum of the means and the variance is the sum of the variances. The mean of the change during 2 years in the variable we are considering is, therefore, zero and the variance of this change is 2.0. Hence, the change in the variable over 2 years has the distribution ø(0,2). The standard deviation of the distribution is √ 2 .
trying an image
the formula is
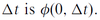
Weiner Process
Properties of Weiner Process
Generalzed Weiner Process
Ito Process
Process for a stock price?
Ito’s Lemma
Derivation of Ito’s Lemma



