FINAL EXAM, HRP 261, WINTER 2021 Flashcards
The following figure shows the results of a study that examined both elbows of 60 baseball players to look for nerve displacement. 32 players had no nerve displacement in either elbow; 3 had a displacement in the elbow of their non-dominant arm only; 14 had a displacement in the elbow of their dominant arm only; and 11 had displacements in both elbows.
Which of the following represents a correct analysis of the data pictured in the Figure?
- 14 of 60 (23.3%) participants experienced nerve displacement in the dominant elbow only whereas 3 of 60 (5%) participants experienced nerve displacement in the non-dominant elbow only (Fisher’s exact test: p=.0073).
- Hand dominance was a significant risk factor for nerve displacement, with an odds ratio of 8.38 (95% CI: 2.02 – 34.77; p=.0034).
- Displacement was significantly more common in dominant elbows (25/60, 41.7%) than in non-dominant elbows (14/60, 23.3%), (Chi-square test: p=.032).
- 14 participants experienced nerve displacement in their dominant arm only whereas 3 participants experience nerve displacement in their non-dominant arm only (Binomial p-value: p=.013).
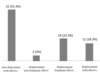
- 14 participants experienced nerve displacement in their dominant arm only whereas 3 participants experience nerve displacement in their non-dominant arm only (Binomial p-value: p=.013).
The following figure shows the results of a study that examined both elbows of 60 baseball players to look for nerve displacement. 32 players had no nerve displacement in either elbow; 3 had a displacement in the elbow of their non-dominant arm only; 14 had a displacement in the elbow of their dominant arm only; and 11 had displacements in both elbows.
The researchers want to use a regression model to simultaneously test the relationships of age, height, main playing position (pitcher or not), and dominant versus non-dominant elbow with the outcome of nerve displacement. Which model should they use?
- Conditional logistic
- Unconditional logistic
- Generalized estimating equation
- Multinomial logistic
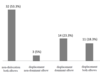
- Generalized estimating equation
The following data result from a study that looked at the effects of physical activity and screen time on the outcomes of anxiety, depression, psychopathological symptoms, and poor sleep. We will focus on the outcome of depression (“Depressive”).
The n (%) values shown give the n (%) of people who have the outcome in each subgroup. For example, 214 people in the low PA/high screen time group are depressive, and this represents 23.1% of the low PA/high screen time group, meaning that there are 214/.231=926 participants with low PA/high screen time.
The crude ORs come from logistic regression models that include as predictors: screen time (low vs. high), physical activity (high vs. low), and their interaction. For example, the logistic regression model that was used to calculate the crude OR values for depression was:
logit(depressive) = α + β screen time (1 if low screen time, 0 if high screen time) + + β physical activity(1 if high PA, 0 if low PA) +β screen time x PA (1 if low screen time AND high PA, 0 otherwise).
What is the intercept (α) of the logistic regression model for depression (depressive) that is given above?
a. -1.20
b. -1.43
c. -1.80
d. -1.47
a. -1.20
The following data result from a study that looked at the effects of physical activity and screen time on the outcomes of anxiety, depression, psychopathological symptoms, and poor sleep. We will focus on the outcome of depression (“Depressive”).
The n (%) values shown give the n (%) of people who have the outcome in each subgroup. For example, 214 people in the low PA/high screen time group are depressive, and this represents 23.1% of the low PA/high screen time group, meaning that there are 214/.231=926 participants with low PA/high screen time.
The crude ORs come from logistic regression models that include as predictors: screen time (low vs. high), physical activity (high vs. low), and their interaction. For example, the logistic regression model that was used to calculate the crude OR values for depression was:
logit(depressive) = α + β screen time (1 if low screen time, 0 if high screen time) + + β physical activity(1 if high PA, 0 if low PA) +β screen time x PA (1 if low screen time AND high PA, 0 otherwise)
What is the beta coefficient for the interaction term of the logistic regression model for depression that is given above?
a. - 0.71
b. - 0.62
c. - 0.62
d. - 0.71
c. - 0.62
The following data result from a study that looked at the effects of physical activity and screen time on the outcomes of anxiety, depression, psychopathological symptoms, and poor sleep. We will focus on the outcome of depression (“Depressive”).
The n (%) values shown give the n (%) of people who have the outcome in each subgroup. For example, 214 people in the low PA/high screen time group are depressive, and this represents 23.1% of the low PA/high screen time group, meaning that there are 214/.231=926 participants with low PA/high screen time.
The crude ORs come from logistic regression models that include as predictors: screen time (low vs. high), physical activity (high vs. low), and their interaction. For example, the logistic regression model that was used to calculate the crude OR values for depression was:
logit(depressive) = α + β screen time (1 if low screen time, 0 if high screen time) + + β physical activity(1 if high PA, 0 if low PA) +β screen time x PA (1 if low screen time AND high PA, 0 otherwise)
Which of the following is a term that appears in the likelihood function that would be used to fit the logistic regression model for depression that is given above? (ST=screen time; PA=physical activity; and int=interaction):
Multiple choice options on attached image
d.
The following data result from a study that looked at the effects of physical activity and screen time on the outcomes of anxiety, depression, psychopathological symptoms, and poor sleep. We will focus on the outcome of depression (“Depressive”).
The n (%) values shown give the n (%) of people who have the outcome in each subgroup. For example, 214 people in the low PA/high screen time group are depressive, and this represents 23.1% of the low PA/high screen time group, meaning that there are 214/.231=926 participants with low PA/high screen time.
The crude ORs come from logistic regression models that include as predictors: screen time (low vs. high), physical activity (high vs. low), and their interaction. For example, the logistic regression model that was used to calculate the crude OR values for depression was:
logit(depressive) = α + β screen time (1 if low screen time, 0 if high screen time) + + β physical activity(1 if high PA, 0 if low PA) +β screen time x PA (1 if low screen time AND high PA, 0 otherwise)
Does it appear that there is any meaningful interaction between physical activity and screen time for the outcome of depression (pay attention only to the pattern of effect sizes; don’t worry about statistical significance).
a. No, because the effect of low screen time on depression is the same regardless of physical activity.
b. No, because the effect of high physical activity on depression is the same regardless of screen time.
c. Yes, because the effect of the combination of high physical activity and low screen time on depression is less than would be expected based on the individual effects of these variables.
d. Yes, because high physical activity and low screen time appear to be synergistic in protecting against depression.
c. Yes, because the effect of the combination of high physical activity and low screen time on depression is less than would be expected based on the individual effects of these variables.
The following table appeared in a paper on predictors of myocardial infarction (heart attack). How would you advise the authors?
a. No changes are needed—the model looks great since it yields highly significant p-values.
b. The authors should collapse the age groups into age<=17 years versus age>=17 years to increase the precision of the odds ratio confidence intervals for age, since the confidence intervals for age are too wide.
c. The authors should run a larger study because it is apparent from the values listed in the table that the sample size and/or event number must have been extremely small.
d. The authors should exclude 0-17 year-olds, because the number of events in this age group is extremely sparse.
d. The authors should exclude 0-17 year-olds, because the number of events in this age group is extremely sparse.
Researchers conducted a randomized controlled trial to evaluate the impact of an intensive injury prevention program on n=840 athletes. Of those assigned to the intensive intervention program, only 10% complied with the intervention. All athletes randomized to the control continued with their normal exercise routines. The following table shows the trial results analyzed according to an intention-to-treat analysis versus an instrumental variable analysis (in which randomization in the RCT is considered the instrument).
There is a problem with the instrumental variable analysis. What is it?
a. Observed compliers may not be “compliers” in the instrumental variable sense; therefore, the IV effect should not be calculated by subtracting the injury risks in observed compliers versus observed non-compliers.
b. A cumulative risk difference cannot be negative.
c. There must be a math error, because the p-value for an instrumental variable analysis will always be smaller than the p-value from the corresponding intention-to-treat analysis.
d. The authors have calculated the observed risks in the complier and non-complier groups, but this is insufficient—we need to know the observed risks in the complier, defier, always taker, and never taker groups.
a. Observed compliers may not be “compliers” in the instrumental variable sense; therefore, the IV effect should not be calculated by subtracting the injury risks in observed compliers versus observed non-compliers.
The authors report the estimated effect from their instrumental variable analysis as -52.5%, but this estimate is incorrect. What is the correct IV estimate?
a. +52.5%
b. -31.0%
c. -44.9%
d. -62.0%
b. -31.0%
Researchers built a propensity score model to predict treatment with drug A (treatment=1) versus drug B (treatment=0). The propensity score model had a C-statistic (area under the ROC curve) of 65%. The researchers plotted the distribution of the propensity groups in the two groups. Which of the following plots is most likely the actual plot of their data?
d.
Which of the following is a bootstrap sample of the following set:
{A, A, B, C, D, E, E, F}?
a. A, A, A, B, C, D, E, E, F
b. A, B, B, D, D, E, E
c. B, B, C, D, E, E, E, F
d. A, A, A, C, D, E, F, G
c. B, B, C, D, E, E, E, F
Examine the following small dataset (attached). 4 subjects had the outcome and 4 did not. The variable “Predicted” represents their predicted probability of having the outcome, based on a logistic regression model.
These data would translate to which of the following ROC curves?
a.
I have data on collegiate cross country runners. The runners were followed prospectively for up to 4 years. Each year, researchers counted the number of times an athlete incurred a stress fracture within that year. Many athletes had multiple fracture per year, some up to 4 fractures in a single year. The goal of the study was to determine predictors of stress fractures. The data are entered as one row of data per athlete per year.
The distribution of the outcome variable is best described as:
a. Poisson
b. Binomial
c. Multinomial
d. Uniform
a. Poisson
I have data on collegiate cross country runners. The runners were followed prospectively for up to 4 years. Each year, researchers counted the number of times an athlete incurred a stress fracture within that year. Many athletes had multiple fracture per year, some up to 4 fractures in a single year. The goal of the study was to determine predictors of stress fractures. The data are entered as one row of data per athlete per year.
Many athletes contributed multiple years of data to the dataset, so the observations are correlated. I ran two regression models with yearly fracture count as the outcome and sex (male vs. female) as the predictor. In one case, I correctly accounted for correlation within athlete; and in one case I neglected to account for correlation within athlete.
Here are the two sets of results (attached).
Which model, A or B, correctly accounts for the correlation?
a. A
b. B
c. The effect of accounting for correlation cannot be predicted.
a. A
You randomly assign 100 husband-wife pairs experiencing marital difficulties to a couples intervention (n=50 pairs) or a control condition (n=50 pairs). The outcome of interest is the development of depression within 6 months (a binary outcome). If you want to analyze these data with a regression model, you should choose:
a. Ordinary logistic regression
b. A GEE model with a binomial distribution and a logit link
c. A GEE model with a Poisson distribution and a log link
d. Conditional logistic regression
b. A GEE model with a binomial distribution and a logit link
The following figure shows a cumulative logit plot. The predictor is a Risk Score (the Triad Risk Score) that ranges from 0 to 2. The outcome is a depression score modeled as an ordinal variable: 0=no depression (reference); 1=mild depression; 2=moderate depression; and 3=severe depression.
The researchers fit an ordinal logistic regression with depression as the ordinal outcome and triad risk score as the ordinal predictor (and no other variables in the model). This model will yield a single odds ratio for triad risk score. Approximately what will the value of this odds ratio be?
a. 2.1
b. 3.4
c. 1.3
d. 4.8
a. 2.1
The following figure shows a cumulative logit plot. The predictor is a Risk Score (the Triad Risk Score) that ranges from 0 to 2. The outcome is a depression score modeled as an ordinal variable: 0=no depression (reference); 1=mild depression; 2=moderate depression; and 3=severe depression.
The researchers fit an ordinal logistic regression with depression as the ordinal outcome and triad risk score as the ordinal predictor (and no other variables in the model). How many parameters does the model have?
a. 1 intercept and 2 beta coefficients
b. 2 intercepts and 1 beta coefficients
c. 3 intercepts and 2 beta coefficients
d. 3 intercepts and 1 beta coefficient
d. 3 intercepts and 1 beta coefficient
The following figure shows a cumulative logit plot. The predictor is a Risk Score (the Triad Risk Score) that ranges from 0 to 2. The outcome is a depression score modeled as an ordinal variable: 0=no depression (reference); 1=mild depression; 2=moderate depression; and 3=severe depression.
The researchers then fit a multinomial logistic regression with depression treated as a categorical outcome and triad risk score as the ordinal predictor (and no other variables in the model). How many parameters does the model have?
a. 3 intercepts and 3 beta coefficients
b. 2 intercepts and 1 beta coefficients
c. 3 intercepts and 2 beta coefficients
d. 3 intercepts and 6 beta coefficients
a. 3 intercepts and 3 beta coefficients
The following figure shows a cumulative logit plot. The predictor is a Risk Score (the Triad Risk Score) that ranges from 0 to 2. The outcome is a depression score modeled as an ordinal variable: 0=no depression (reference); 1=mild depression; 2=moderate depression; and 3=severe depression.
Among those participants that have a cumulative risk score of 2, approximately how many have a depression score of 0?
a. 45%
b. 35%
c. 20%
d. 5%
c. 20%
