Exchange Economies

Question 1

What is a monotone preference?

Answer 1

This is when the consumer’s utility rises as any one of the quantity of consumption bundles increases. It is an ever-increasing preference.

Question 2

What is a convex preference?

What is defined as a convex set?

Answer 2

This is a preference in which the average consumption between two bundles is preferred, rather than the extreme (which would be equivalent to picking all of either good). This preference exists due to diminishing marginal utility and usually only exists within populations, rather than individuals.

A convex set is one where if you a draw a line between two points, the line drawn would stay in the set. A non-convex set would have some of the line drawn outside of the set (think of the ‘set’ as a badly drawn circle).

Question 3

What utilities are strictly convex?

Answer 3

Cobb-Douglas utilities (normal indifference curve - curved) are strictly convex.

For a line to be strictly convex, the average bundle has to be preferred to the extreme bundles. That is to say that, for two consumers, they would rather pick the weighted average because picking an extreme would make either one of them have less utility for one good. This is because of diminishing marginal utility.

But, for linear utilities (diagonal downward slope), we can say that the preferences are not strictly convex because the MRS is constant. Regardless of what either consumer picks, they would be indifferent to the weighted average.

Question 4

What does a Cobb-Douglas utility function look like?

Answer 4

See image.

Question 5

What is a monotonic transformation?

Answer 5

This is when the utilities derived from each bundle may change but the order of preferences still stay the same. We can do this by :

• Multiplying by a constant (although not a negative or a 1/ fraction)
• Raising by a power
• Taking the natural log.

To understand if a monotonic transformation has taken place, first work out what the change has been (has the utility function been divided by 2). Then write this down as g(u) = 1/2 u. Then differentiate that function with respect to u and you will see that 1/2 > 0, and thus the function is rising and so a monotonic transformation.

Question 6

What is the MRS of good 1?

How do we calculate it?

Answer 6

This is the amount of good 2 that the consumer is willing to give up in order to get more of good 1 (depending on whichever good is on bottom of the MRS equation). The equation is given below :

Question 7

What is the Edgeworth box?

Answer 7

The Edgeworth box allows us to graphically represent a market of two commodities between two consumers. Therefore, it also shows us their indifference curves too in which we can analyse their preferences.

Every allocation within and on the Edgeworth box is deemed to be initially feasible (we will use feasible in this course as there is no waste, the total of what was allocated initially will remain the same after looking at preferences).

Think of Agent A starting in the bottom left and agent B starting at the top right. Thus, their consumption also follows the same pattern - i.e agent B consumption is the distance to the endowment from the top right.

Question 8

What is the endowment allocation in an Edgeworth box?

Answer 8

This is where no trade occurs (initial bundle).

Note: The total quantity of good 1 used is along the bottom and the total quantity of good 2 is shown vertically (remember there are 2 consumers consuming 2 goods).

Question 9

Are boundary points within the Edgeworth box feasible?

Answer 9

Yes.

• Any point on the bottom would mean that Agent A has none of good 2.
• Any point on the left boundary would mean that Agent A has all of good 2.
• Any point on the top would mean that Agent B has none of good 2.

Question 10

How can we graphically represent the preferences of both agents in the Edgeworth box?

Answer 10

• Remember that Agent B preferences are shown from the top right-hand side. Thus, Agent B indifference curve is ‘flipped’ in a sense. But, the notion holds true that agent B’s utility would increase the more consumption he has.

Question 11

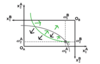
What is a pareto-improvement?

Answer 11

This is when the utility of neither consumer decreases but simultaneously the utility of either consumer (or both) will increase from the initial endowment.

Note that the term ‘Pareto improvement’ is with respect to the initial endowment.

Image: In the black area, they are strictly better off.

On the green line, Agent A is indifferent with regards to the initial endowment but agent B is strictly better off.

The reverse is true for any point on the grey line in the set that the indifference curves meet.

Question 12

Graphically, what would an improvement in trade look like given that we have a coming together of two indifference curves in the Edgeworth box?

Answer 12

Question 13

When should both agents stop trying to ‘improve their trade’?

Answer 13

When it makes either one of them worse off. There will come a point where the edges of the indifference curve are touching each other - do not mistake this as being tangent. This is when any further movement will make one agent worse off and the other better off (which is not a pareto-improvement).

When no further pareto-improvements can be made, we call it ‘Pareto-optimal’.

Question 14

What is the ‘contract curve’?

Answer 14

This is the line that joins all the ‘Pareto-optimal’ points.

It is called the contract curve because the agents should come to an agreement on trade at a point that lies on this contract curve.

Note: even though we class all the points on the contract curve as ‘Pareto-optimal’, it does not mean that it is fair. For example, picking a point on the contract curve that lies to the bottom left will result in a greater utility for Agent B as he consumes more of each good.

Question 15

What are the three conditions required to suggest that ‘Pareto-optimal points occur where the indifference curves are tangent’?

Answer 15

1. The preferences need to be convex. (as this is all about trade and so weighted averages are needed). (non-convex also indicates that there is more than one tangency point).
2. The preferences need to be smooth. (this is not the case for things like perfect complements - again, cannot determine optimal trade where a consumer is indifferent to consuming one more of a good).
3. Tangency points need to occur internally (any point on the boundary is feasible, but not optimal).

Question 16

Assuming we have smooth and convex preferences that lie inside the Edgeworth box, how can we confirm that a point is Pareto-optimal?

Answer 16

By calculating the MRS of both agents and setting them equal to each other. The point where they are equal is a Pareto-optimal point.

Question 17

What can be said about Cobb-Douglas utility functions and efficiency (think boundary points)?

Answer 17

Remember that any point on the Edgeworth box boundary is feasible, but not always efficient.

The only points where we can say that it is efficient (i.e. no one is made worse off is the origin of both Agent A and B).

As moving along the indifference curves at any other boundary point could make either agent better off.

Question 18

How do we find the equation for the contract curve given the following allocations?

Answer 18

• Find MRS of both agents and equate them to each other. (efficient points)
• Total both quantities of goods to determine feasibility.
• Sub these feasible quantities into the efficient points equations to give contract curve equation.

The answer for this one should give us precisely the diagonal for the square of the Edgeworth box - as we have shown that xa2=xa1

Question 19

What is the core?

Answer 19

With respect to the endowment, it is the set of all Pareto-optimal points (on contract curve) that are Pareto improvements (wrt initial allocation). Thus, in the core, both agents have to be at least as well off as they were wrt initial allocation.

Highlighted in bold to remember.

Note: Even if it is Pareto-optimal, trades can still be blocked by either agent depending on which way go along the contract curve.

This is all the points in the contract curve within an indifference set (where both indifference curves meet) which will not be blocked by either agent.

Question 20

How do we find the core, given the following worked out contract curve?

Answer 20

Remember, the core is the set of all Pareto optimal points (and thus on contract curve) that are Pareto improvements with respect to the endowment allocation (has to be at least as good as).

Question 21

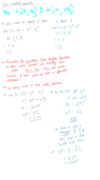
Find the contract curve and core of this non-symmetric CD function below :

Answer 21

Question 22

Why are we not able to find the MRS for perfect complement preferences?

Thus, what do we do?

Answer 22

This is because the preferences are not smooth. They have a kink point at which increasing the quantity of either good by 1 would not increase the utility for the consumer.

But, we can say that an efficient allocation for any consumer with goods that complement is where he has the same amount of each good (x1=x2) - as increasing the quantity of either good by 1 will not increase his utility (but will increase agent B).

Note: this can only be true when the utility of agent B is increasing with more consumption (e.g. in the case where agent B has perfect substitutes).

Also, if agent B has 0 of either good, it is also not an efficient allocation.

Question 23

What are quasi-linear preferences?

Answer 23

These are preferences in which one function can be anything (usually non-linear) and the other function is linear.

Another thing to note is that indifference curves are always vertical/horizontal translates, depending on the arbitrary non-linear function.

Since it is only the non-linear part of the function that can be differentiated (as it is a multiple), we can also say that the MRS is independent of the second variable.

If you are reasonably wealthy, you won’t usually check your preference between buying an extra loaf of bread and saving that money (bread and money being the two goods). Thus, a quasi-linear preference is shown here. Obviously will not be the same preferences if you live in poverty.

Question 24

What are the key things to note when dealing with quasi-linear preferences (wrt trying to derive a contract curve)?

Answer 24

• Feasibility can only be calculated for good 1 (as it does not matter how much of good 2 you have, it has no effect). Do this after equality of MRS’.
• Thus, when setting the MRS’ equal to each other, you find out the quantity of good 1 that would be pareto-optimal.

Then, depending on what you were given at the start, you can start to calculate how much of good 1 would be pareto optimal for agent B to hold.

Forget about good 2 for quasi-linear preferences.

Question 25

What can we say about the contract curve of linear utilities? Proceed to explain how we find the core.

Answer 25

The contract curves are always on two edges of the Edgeworth box. Work out the MRS of both agents and determine which agent has the higher MRS. If MRSA \> MRSB, that means that agent A is more of a good 1 lover and agent B is more of a good 2 lover. Also, since the MRS is constant, they should continue to trade until Agent A consumes all of good 1 and agent B consumes all of good 2 - **leaving a contract curve that is all of the bottom and right of the Edgeworth box.** Now, to explicitly find the core, we need to find the feasible points and ensure that the utilities of the allocation is at least as good as the initial bundle. In the lecture example, the endowment utility is given as 6 for agent A. To reach this again with the current utility (just for good 1) , agent A needs to consume at least 3 of good 1 and of course 0 of good 2 (hence the core position). We do the same for Agent B and good 2. We have xa1 and xa2, we also have xb1, we need xb2. To get this, we use the same process to get xb2 = 24/9. **BUT** remember that agent B holds all of good 2 and so the pareto optimal points that are also considered improvements will lie where it is 4 (how much B holds) minus 24/9. This gives xb2 as 4/3.

Question 26

What is a good definition for the budget set in terms of consumption and endowment?

Answer 26

That is to say that the set of bundles that are non-negative in consumption and never greater than the initial endowment. i.e. the value of the bundle he ends up ( price x quantity) with cannot exceed the value of the bundle that he was initially allocated. In practice, we will assume that the consumer achieves equality in terms of utility derived from initial bundle and stated bundle.

Question 27

When is utility maximisation for a consumer achieved?

Answer 27

When his indifference curve is tangent to the budget set.

Question 28

What is the relative price?

Answer 28

This is the price of one good in direct comparison with another - it is the ratio of prices (p1/p2).

Question 29

What is a price- taker?

Answer 29

A price-taker is anyone who cannot affect the prices in a market due to his/her consumption or production. This is because there may be many competitors in the market and so their demand or supply decisions will not have a huge effect on the market.

Question 30

When can we say that a 'general equilibrium' has been reached in the market?

Answer 30

This occurs when - the market has cleared - i.e the allocation is feasible (endowment quantity has been used) - both consumers are maximising their utility, with prices taken into consideration. Thus, we can say that it is important for us to look at both (relative) prices and the quantity allocation in order for us to receive a general equilibrium.

Question 31

When does utility maximisation for both consumers occur?

Answer 31

When MRSa = MRSb = p1/p2 Remember, the negative ratio of prices is the slope of the budget set. The MRS' of both consumers' is their indifference curves. Utility maximisation is achieved when the indifference curve is tangent to the budget set, given that preferences are smooth, convex and internal.

Question 32

What are the steps to solve for symmetric CD preferences to get general equilibrium?

Answer 32

- Find where utility is maximised for both consumers. This is where MRSA = MRS B = p1/p2. (Just find a solution for xa2) - Now, we need to determine when this is feasible, i.e. used all his wealth. This is where p1x1+p2x2= p1w1 +p2w2, budget set is maximised. Sub xa2 in here. - From this, we can use the endowment allocation numbers and sub in to get a price ration/ - Again, sub this price ratio back in and you should get 4 equal numbers as this is symmetric CD preferences.

Question 33

What is Walras' law?

Answer 33

This states that for in any market where a good is in excess demand, the other good will be in excess supply, thus always creating an equilibrium, taking into account market prices. Thus, the 'invisible hand' will raise prices when there is excess demand and will also lower prices when there is excess supply.

Question 34

What is the first fundamental welfare theorem?

Answer 34

In any competitive market economy, there will always be a general equilibrium that is Pareto efficient. - holds true even in cases where there is not a need for convex, smooth preferences (see image), different derivation in this case.

Question 35

What is the second welfare theorem?

Answer 35

This states that we can gain an equilibrium point (Pareto-optimal) by allocating/re-distributing wealth and then letting the 'invisible hand' do its work. Redistributing wealth/ allocation after transfers can be performed by regulators through the use of taxes, subsidies etc. Note: Here, preferences HAVE to be convex as we will be unable to gain a Pareto-optimal point once we consider the distribution of wealth (see the difference between slide 82 and slide 89).

Question 36

What does linear utilities mean for MRS?

Answer 36

This means that the MRS remains constant. For example, the MRS for purchasing milk would remain constant as the prices would not change in a store. The rate at which you are willing to trade does not depend upon how much of the good you currently own (no diminishing returns to utility).

Question 37

Will a consumer want to increase or decrease his consumption of good 1 if p1/p2 \< MRS?

Answer 37

Increase. He is willing to trade 2 units of good 2 to get good 1 but now, he can get good 1 for giving up only one unit of good 2 and so thus his consumption of good 1 would increase.

Question 38

When do markets clear for linear utility preferences?

Answer 38

When the price ratio is in between the MRS' of both agents. It cannot be lower than both agents MRS' as this would mean that both agents would just want as much good 1 as possible (vice versa for MRS greater than and good 2).

Question 39

Relating exchange economies to borrowing and lending, what do we call good 1 and good 2?

Answer 39

Good 1 (xa1) is current consumption (i.e. income today) and Good 2 (xa2) is future consumption (income tomorrow). Wa1 is income today and wa2 is income tomorrow. Thus, the budget equation would be something like xa1 + ((1/1+r) \* xa2) = wa1 + ((1/1/+r)\*wa2). Consumption = Income

Question 40

Why do we multiply the good 2's (future consumption and future income) by the interest rate?

Answer 40

If I am willing to give up a unit of income tomorrow, it is worth today to me what it will be tomorrow multiplied by the interest rate. Why? As today, I could have invested that money and with the interest rate, received tomorrow's income. If struggling, relate it to price ratio in normal budget equation.

Question 41

If wa1 - xa1 is negative, what does this mean in the 'borrowing and lending' economy?

Answer 41

This means that the consumer is a borrower as the consumption exceeds the income. The reverse would be true (i.e. would be a lender) if the consumption did not exceed the income - wa1-xa1 = +ve

Question 42

Work out the following

Answer 42

- Make sure it is in CD form. Apply monotonic transformation if necessary. - Using demand functions to get xa1 and xa2 (efficient) - Equate these two to the total income (wa1+wb2). - You can work out real interest rate from here. Remember that the price ratio is the same as 1+r. (p1/p2=1+r) - Also write p2/p1 as p for simplicity in calculating feasible demands. - Sub in p2/p1 into demand functions. If value is less than income (wa1 or wa2), then consumer is lender

Question 43

With regards to insurance (or security exchanges), what does good 1 and good 2 represent?

Answer 43

Good 1 represents State 1 - this is the 'norm' state of consumption where everything is fine. For example, your health is fine regarding health insurance. (pi) Good 2 represents State 2 - this is the state of consumption where things are not so certain. So your health is decreasing in this state. (1-pi) The utility that each consumer gets is from their money, which of course is subject to a budget constraint.

Question 44

What does p1/p2 (relative price mean)?

Answer 44

This is how many units of good 1 would be given up in order to get good 2. In the case of securities, it would be how much I willing to give up my current consumption to get future consumption. Note: this is just one division. The MRS is differentiation (so two divisions) hence why MRS is how many units of good 2 would be given up in order to get good 1.

Question 45

What does 'no aggregate risk' mean? What does this mean for the Edgeworth box?

Answer 45

This means that when entering a deal for securities, the initial state for both consumers provides the same income as the final state. (wa1+wb1=wa2+wb2) Hence, there will be no risk for any agent to lose money. It means that the Edgeworth box will be a square and that the certainty line will be a diagonal for both agents from their respective origins.

Question 46

What is the 'certainty line'?

Answer 46

This is the bundle of goods for each agent that he is absolutely sure that he will consume. This holds true because the certainty line signifies where the agent consumption is equal in both states. Where there is no aggregate risk, the certainty lines of both A and B are diagonals across the Edgeworth box.

Question 47

What does it mean for a deal to be 'actuarily' fair?

Answer 47

This means that both agents are not expected to make any gains from the deal. On some bundles, there will be winners and losers but across an average, there should be no gains made. This occurs when the MRSA=MRSB=p1/p2 The price ratio in the case of the lecture examples has been worked out as pi/1-pi. This happens in cases where the income is not affected by external factors and so thus a fair deal can be made (say a deal of insurance between me and a friend).

Question 48

When will aggregate uncertainty occur?

Answer 48

This occurs when one of the agents has either a greater or lower income in either of the two states. Thus, the total endowment is not equal to the total allocation in another period. For example, if i was to enter into an insurance deal with a health insurance company : - A consumer in state 1 may be healthy initially but very unhealthy later on. Thus his income wa1\> wa2 as in the future he is not able to work as much and so less income. - The insurance company still has the same income. regardless of health as it is not a physical being. Thus, wb1=wb2. BUT, wa1+wb1 does not equal wa2+wb2.

Question 49

What does it mean to be 'risk neutral'?

Answer 49

This usually occurs for large firms entering a deal with a small number of individuals. Even though the risk individually might be high, because they have so many individuals in deals, the risk will average out. e.g. insurance companies. So risk-neutral agents will take on all the risk whilst the risk-averse individual is fully insured to reach a point where it is optimal for both agents. Note: This will not happen under asymmetric information (where an agent will know details about the future state, like health, of themselves).

Question 50

Will the certainty lines of both agents meet when there is aggregate uncertainty?

Answer 50

No, because now the Edgeworth box will not be a square as income from both states will not be the same, hence the added risk. We expect that one agent will take on all the risk (because they can due to size and averaging out) and the smaller agent will be fully insured at the optimal point. The optimal point is where indifference curves and the certainty line (s) meet. Again, this will be actuarily fair as both agents expected loss = expected gains (as an aggregate).