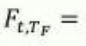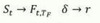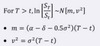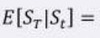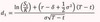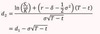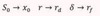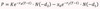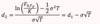Exam MFE Flashcards
(156 cards)
PCP for Stock

PCP for Exchange Options

Exchange Option Duality
C(A,B) = P(B,A)
PCP for Currency Exchange
Substitutions:
S ⇒ ?
r ⇒ ?
δ ⇒ ?
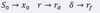
Bounds for Put Price
Rank the following:
- PEur 2. PAmer3. Max(0, Ke^(-rt) - FP(S) ) 4. K
K ≥ PAmer≥ PEur ≥ Max(0, Ke^(-rt) - FP(S) )
Bounds for Call Price
Rank the following:
- CEur 2. CAmer3. Max(0, FP(S) - Ke^(-rt)) 4. S
S ≥ CAmer≥ CEur ≥ Max(0, FP(S) - Ke^(-rt))
Rules for Early Exercise - American Call
Nondividend Stock = ?
Dividend Stock = ?
Nondividend Stock
Never Optimal
Dividend Stock
Optimal if PV(Divs) > PV(Int on Strike) + Implicit Put
Rules for Early Exercise - American Put
Nondividend Stock =
Dividend Stock =
Early Exercise is optimal if:
PV(Interest on Strike) > PV(Divs) + Implicit Call
Call Options Prices
Given K1 < K2 < K3, what 3 things do you know about call prices?
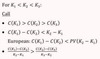
Put Option Prices
Given K1 < K2 < K3, what 3 things do you know about put prices?
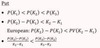
An option can be replicated by buying ___ shares of the underlying stock and lending ___ at the risk free rate.
An option can be replicated by buying Δ shares of the underlying stock and lending B at the risk free rate.
Replicating Portfolio
Δ = ?
V = payoff of the option

Replicating Portfolio
B = ?
V = payoff of the option

Currency Exchange Duality

Replicating Portfolio
For Calls, Δ is (+/-) and **B **is (+/-)?
For Puts, Δ is (+/-) and B is (+/-)?
For Calls, Δ is (+) and B ** is (–**)?
For Puts, Δ is (–) and B ** is (+**)?
Risk Neutral Probability Pricing
p* = ?

Risk Neutral Probability Pricing - Option Price Formula
Option Price (V) = ?

Realistic Probability Pricing
p = ?
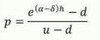
Realistic Probability Pricing
Option Price (V) = ?
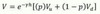
Realistic Probability Pricing
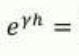
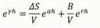
Forward Tree
If u and d are not given,
u = ?
d = ?
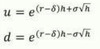
Cox-Ross-Rubinstein Tree
u = ?
d = ?
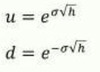
Lognormal Tree (Jarrow-Rudd Tree)
u = ?
d = ?

In the Binomial model, how can you tell if arbitrage is available?
Arbitrage is available if the following inequality is not satisfied: