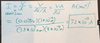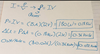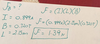Exam 1 Chapters 19-22 Flashcards
(47 cards)
What is the difference between a conductor and an insulator?
Conductor- Usually metal, has 0 electric field, has free charges
Insulator- Usually non metal, has an electric field, has NO free charges
What does Coulomb’s law state?
Where
F= ma (mass x acceleration)
Q and q= Charges
r= Distance between the two charges
k= 8.99 x 10^9 (N x m^2/C^2)

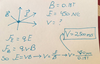
The attractive force between the point charges 8.44E-6C and Q has a magnitude of 0.975N when the separation between the charges is 1.31m Find the sign and magnitude of the charge Q.
Q= 2.2E-5

Given that Q1= +12uC and d= 0.16m, find the direction and magnitude of the net electrostatic force exerted on the point charge q1

F1= F(1,2) + F(1,3)
F1= [k(+q)(2q) / (d^2)] + [k(+q)(3q) / 2(d^2)]
F1= [8.99E9(1 x 12E-6)(-2 x 12E-6) / (0.16^2)] + [8.99E9(1x 12E-6)(3x 12E-6) / (2 x0.16^2)]
F1= -101.13 + 37.89
F1= 63.24 (Would be negative to specify direction)
Suppose that a charge q2 can be moved left or right along the line connecting the charges q1 and q3. Given that q= +12uC, find the distance from q1 where q2 experiences a net electrostatic force of 0. The charges q1 and q3 are separated by a fixed distance of 0.32m.

Distance between 1 and 2= ? (X)
Distance between 1 and 3= (.32m-X)
F2= F(2,1) + F(2,3) BUT where F2=0
0= [k(-2q)(1q) / x^2] + [k(-2q)(3q) / (0.32m-x)^2]
- [k(-2q)(1q) / x^2] = [k(-2q)(3q) / (0.32m-x)^2]
(k’s and -2q’s cancel eachother out)
- [(1q)(0.32m-x)^2] = [(3q)(x^2)] > Do 3q/q= 3 and take square root
- (0.32m-x) = sqrt3(x)
x= (0.32m)/ 1 +- sqrt 3
x= 0.12 and -0.45
Find the orbital radius for which the kinetic energy of the electron in example 19-1 is 1.51 ev.
*1ev = 1 electron volt = 1.6E-19
* F electrical = F centripetal

[k(q1)(q2)/r^2] = ma (centripetal) is equivalent to…
[k(e)^2/r^2] = m (v^2/r) > e is for electron
V^2 = k(e^2)/ (r)(m)
Kinetic energy= (1/2)(m)(v^2)
V^2= (K)(2)/(m) > Set v^2’s equal to each other
k(e^2)/ (r)(m) = (K)(2)/(m)
Where r= k(e^2)/ 2K
r= (8.99E9)(1.6E-19C^2)/ 2(1.51ev)(1.60E-19)
r= 4.76E-10
Four point charges are located at the corners of a square with sides of length a. Two of the charges are +q and two are -q. Find the magnitude and direction of the net electric force exerted on a charge +Q, located t the center of the square, for each of the following 2 arrangements of charge; the charges alternate in sign +q,-q,+q,-q as you go around the square; the two positive charges are on the top corners, and the two negative charges are on the bottom corners.
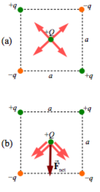
- The first box has a F(net) of zero because the charges cancel out
- F(net)= 2F(x) + 2F(y) where a= Length
F(net)= 2[KqQ/ (a/sqrt2)^2] x sin(45) + 2[KqQ/ (a/sqrt2)^2] x sin(45)
F(net)= [-4(sqrt2)kqQ/ a^2]
What is the equation when charge Q is distributed over a sphere?

What is the magnitude of the electric field produced by a charge of magnitude 7.5uC at a distance of 1m and 2m?
Equation for electric field: E= kq/r^2
- E= [(8.99E9)(7.5)/(1)^2]= 6.74E10
- E= [(8.99E9)(7.5)/(2)^2]= 1.68E10
What is the equation for electric field?
E= k(q)/(r)^2
For point charges, each of magnitude q are located at the corners of a square with sides of length a. Two of the chargess are +q and two are -q. The charges are alternate in sign as you go around the square. The top 2 corners of the square have positive charges (-q,+q). In which case will the electric field at the center of the square have the greatest magnitude? Calculate the electric field at the center of the square for each of these 2 cases.
E= [kq/(1/2)(a^2)]
E1x + E2x + E3x + E4x= [kq/(1/2r^2) 1/sqrt2 +-1/sqrt2 + 1/sqrt2 +-1/sqrt2 = 0
E1y + E2y + E3xy+ E4y= -1/sqrt2 - 1/sqrt2 - 1/sqrt2 - 1/sqrt2 = [-4sqrt2(k)(q)/(r)^2]
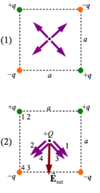
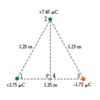
The electric field lines surrounding 3 choices are shown. The center charge is q2= -10uC. What are the signs of q1 and q3? Find q3.

- Charges q1 and q3 must be positive
- The charge q1 has 8 lines leaving it, but q2 has 16 lines entering it. Because 8 is half of 16, and since the number of lines entering or leaving a charge is proportional to the magnitude of the charge, the magnitude of q1, is one-half of q2, or 5uC.
- By the reasoning of part b, the magnitude of q3 is 5uC
A surface encloses the charges q1= 3.2uC, q2= 6.9uC, and q3= -4.1uC. Find the electric flux through this surface.
6.8E-12 Nm^2/C

What is the equation for electric flux?

What is the eqaution of electric field?
E= kq/r^2
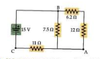
The cell membrane of a typical nerve cell consists of an inner and an outter wall separated by a distance of 0.10um. The electric fields within the cell membrane is 7.5E5. Approximating the cell membrane as a parallel-plate capacitator, determine the magnitude of the charge density on an inner and outer cell walls

A uniform electric field of magnitude 4.1E5 N/C points in the positive x-direction. Find the change in electric potential energy of a 4.5uC charge as it moves from the origin to the points (0,6m) (6m,0) (6m,6m)

What is the difference between electrical potential energy and electrical potential

An electrical plate capacitor has plates separated by 0.00075m. If the electric field between the plates has a magnitude of a.) 1.2E5 V/m or b.) 2.4E4 N/c, what is the potential difference between the plates?

A typical 12V car battery can deliver 7.5E5C of charge. If the energy supplied by the battery could be converted entirely to KE, what speed would give to a 1400kg car initially at rest?

The electrons in a TV picture tube are accelerated from rest through a potential difference of 25,000V. What is the speed of the electrons after they have been accelerated by this potential difference?

A proton has an initial speed of 4E5 m/s. a.) What potential difference is required to bring the proton to rest? b.) What potential difference is required to reduce the initial speed of the proton by a factor of 2? c.) What potential difference is required to reduce the initial kinetic energy of the proton by a factor of 2?

The hydrogen atom consists of one electron and one proton. In the Bohr model of the hydrogen atom, the electron orbits the proton in a circular orbit of radius 0.529E10 m. What is the electric potential due to the proton at the electrons orbit?