Exam 1 Flashcards
Y
Data
Yi
An observation of the data
Y bar
Mean of the data
s2
Variance of the data
s
Standard deviation of the data
µ
Mean
σ2
Variance
σ
Standard deviation
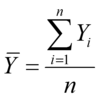
Arithmetic Mean
The average
Most common
Unbiased estimate of µ if assumptions on the earlier slide are met
Geometric Mean
Used when the values are multiplied
Used in population ecology
Harmonic Mean
- Greater weight to extreme small values
Used for rates, and in population genetics to estimate effective population size
Symmetrical Distributions
If the distributions are perfectly symmetrical then the arithmetic mean, median, and mode are equal.
Variance
The variance of the population (σ2) can be estimated from data
Remember that variance is in units2
Standard Deviation
The square root of the variance
On average, s does not change when you increase sample size
Standard Error of the Mean
The standard deviation of the estimated population mean
Decreases when you increase sample size
Coefficient of Variation
- The sample standard deviation divided by the sample mean
Often multiplied by 100 to represent a percent
Classical definition
P=0, outcome will never happen
P=1, event will always happen
Note: typically cannot measure
Frequentist definition
P=0, outcome didn’t occur in any trial
P=1, outcome occurred in every trial
Note: can measure
Experiment
¡A set of trials
¡E.g. all the crocodiles in a nest
Trial
¡Each replicate event
¡E.g. a particular crocodile
Sample space { }
¡The set of all possible outcomes
¡E.g. hatched and didn’t hatch
Outcome ( )
¡A possible result of a event
¡E.g. hatched
Event
¡A process with a beginning and end
¡E.g. hatching of an crocodile
Defining Sample Space
nOutcomes are mutually exclusive
nOutcomes are exhaustive
Axiom 1
The sum of all the probabilities of outcomes within a single sample space = 1.
nComplex events
¡Composites of simple events in the sample space
¡
¡Rolling 3 OR rolling 4
¡First crocodile hatching OR the second crocodile hatching
nShared events
¡Multiple simultaneous occurrences of simple events in the sample space
¡Rolling 1 on the first roll AND 1 on the second roll
¡First AND second crocodile hatch
Axiom 2
The probability of a complex event equals the sum of the probabilities of the outcomes that make up that subset.
Conditional Probabilities
Used to calculate probabilities when you know that an outcome has occurred or will occur
Probability of a given b
Bayes’ Theorem
The conditional probability rewritten in terms of the inverse conditional probability.
Frequency Distribution
nBased on number of observations within a given range
¡Non-negative integers
Probability Distributions
nBased on probabilities and often represented by the density
¡Density is calculated using the area of each bar
¡Thus, densities can be greater than 1
Discrete
nTake on finite numbers
nE.g., integers
Continuous
nTake on any value within a range
nE.g., diameter of your head
Discrete Distributions
nBernoulli
¡Uncommon because of simplicity
nBinomial
¡Common in biological data
nPoisson
¡More appropriate when a successful outcome is rare
Bernoulli Distribution
nA single event
nOnly two outcomes
¡E.g., 0 and 1
nP(1)=p and P(0)=1-p
Binomial Distribution
nMultiple Bernoulli trials
nProbability of successful outcomes
¡E.g. 5 of 10 eggs hatch
nNeed to know
¡Probability of success (p)
¡Number of trials (n)
¡Number of successful trials (X)
Poisson Distributions
nUsed when
¡Number of trials is unclear
¡p is very small
¡Sampling fixed area of space or time interval
nNeed to know
¡Number of observed occurrences (x)
¡Rate parameter (λ)
Rate Parameter
Estimated from experiments or prior data
Represents the average of the Poisson Distribution, and also the variance
Expected Value of the Distribution
Is the mean or average
Variance of the Distribution
The spread of the data
Calculated as the squared deviations from the mean
Continuous Distributions
Uniform Distributions
Used to represent truly random events
Normal Distributions
Extremely common and important in biology (as well as many other fields)
There are lots of other continuous distributions
F, t, Beta, Gamma, Log-normal, exponential, chi-squared, etc.
Problem with Continuous Distributions
Probability for any given value is zero
There are an infinite number of different possibilities
Solution
Calculus and axioms
Axiom 1 state the sum of all probabilities must equal 1.0
So, using integral calculus, we can find the function that satisfies axiom 1
Parameters
Min (a) and max (b)
Uniform Distribution
Probability Density Function (PDF)
Is the function that gives the probability for x
Cumulative Density Function (CDF)
Is a function that gives the area under the curve (i.e. the cumulative probability)
Parameters
Mean (µ) and Standard deviation (σ)
Normal Distribution
Works for any type of distribution
Sum or average random samples from a distribution
Result is a distribution that is normal!
Central Limit Theorem
Lambda and Max of x axis
Poisson Dist.
of trials and probability of success
Binomial Dist
Min and Max
Uniform Dist.
