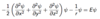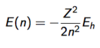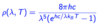Equations

Question 1

State the Rayleigh-Jeans law for energy density.

Answer 1

Question 2

State the equation for energy density.

Answer 2

Question 3

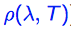
State the equation for heat capacity at lower temperatures according to classical physics.

Answer 3

Question 4

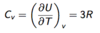
Give the equation for the kinetic energy of electrons in the photoelectric effect.

Answer 4

E_K = 1/2 m_ev² = hv - Ø

m_e: mass of electron

v²: velocity (v = c ÷ wavelength)

Ø = hv = hc/i\

h: energy of photon

c = i\v

Question 5

Give the general form for an eigenvalue equation.

Answer 5

(operator)(eigenfunction) = (eigenvalue)(eigenfunction)

Question 6

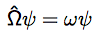
Give the equation for the probability of finding a particle between x₁ and x₂.

Answer 6

Question 7

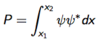
Give the equation for a normalised wavefunction.

Answer 7

Question 8

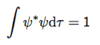
Give the equation for two orthogonal wavefunctions.

Answer 8

Question 9

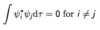
Give the expectation value of an operator (sigma).

Answer 9

Question 10

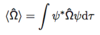
Give the equation for the Heisenberg uncertainty principle.

Answer 10

Question 11

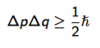
State the Schrödinger equation for a 1-dimensional system.

Answer 11

Answer 12

Question 13

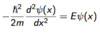
What is h(bar)² equal to?

Answer 13

h(bar)² = h² / 4π²

Question 14

Sketch the wavefunction and probabilty density fot the n=1 and n=2 states of a particle in a infinite well.

Answer 14

Question 15

Sketch and annotate the diagram for a partcile at a finite barrier.

Answer 15

Question 16

Sketch the graph showing the quantum mechanical path of tunneling.

Answer 16

Question 17

Sketch the ground state wavefunction of a harmonic oscillator.

Answer 17

Question 18

Sketch the first excited state wavefunction of a harmonic oscillator.

Answer 18

Question 19

Give the equation for the harmonic oscillator.

Answer 19

V(x) = 1/2 k_fx²

Question 20

Inserting V(x) into the Schrodinger equation gives which allowed energy levels? (2)

Answer 20

E_v = (v + 1/2) h(bar)w

w = (k_f/m)^1/2

v = 0, 1, 2…

m: mass of particule, for diatomics use mu
w: frequency

E_v: vibrational energy

Question 21

Sketch a diagram showing that the particle is more likely to go from ground-ground state to excited-excited state.

Answer 21

Question 22

State Couloumb’s Law.

Answer 22

V = - (Ze²) ÷ (4πe_or)

e_o: permitivity of free space

Z: nuclear charge

Question 23

Give all the quantities that are equal to 1 in atomic units.

Answer 23

• mass of electron m_e
• charge of electron e
• reduced Plank’s constant h(bar) (h/2π)
• Coulomb’s constant 1/4πe_o

Question 24

Write the Schrodinger equation for hydrogen.

Answer 24

Question 25

Give the equation for the energy levels for a one-electron atom or ion with nuclear charge Z_e.

Answer 25

Question 26

State the electronic wavefunctions for H.

Answer 26

where alpha = spin up (1/2)

where beta = spin down (-1/2)

Can also be written as:

• 1s(1)alpha(1) ⇒ 1s_alpha(1)
• 1s(1)beta(1) ⇒ 1s_beta(1)

Question 28

When does a wavefunction for electrons obey the Pauli principle?

Answer 28

wavefunction(1,2) = -ve wavefunction(2,1)

Question 29

Give the quantized equation for electronmagnetic radiation energy.

Answer 29