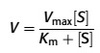Equations

Question 1

Fick’s Law

Answer 1

The net rate of diffusion is proportional to the diffusion co-efficient (1/ square root of MW) , surface area, concentration gradient and inversely dependant on thickness of the boundary

Question 2

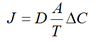
Nernst Equation

Answer 2

Equlilibrium potential – the membrane potential at which electrical and chemical gradient of individual ions are equal. For cations, o/i. For anions i/o.

Question 3

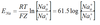
Goodman equation

Answer 3

The membrane potential depends on the distribution of and the membrane permeability to Na, K, Cl.

Question 4

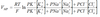
Pouseuille’s law

Answer 4

n = viscosity

Question 5

Reynolds number

Answer 5

Re >2000 is turbulent

Question 6

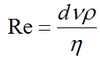
Henderson

Answer 6

At 37°, Ka x 0.03 = 24

Question 7

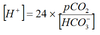
Henderson Hasselbalch

Answer 7

pKa=6.1 at 37°

Question 8

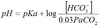
Standard deviation

Answer 8

SD = √variance.

Measure of dispersion or spread of a normal distribution.

95% of data points lie within 1.96 SD of the mean.

Question 9

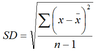
Chi square

Answer 9

Difference in observed from expected in nominal data, based

on contingency table. Compares rates or proportions.

Question 10

Shunt equation

Answer 10

Calculated to give estimate of venous admixture – gives ‘virtual shunt’, the amount of shunt which would be present if the shunt was entirely of mixed venous blood.

Question 11

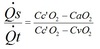
Laplace’s law

Answer 11

T=surface tension

Question 12

Force

Answer 12

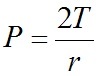
Force = Pressure X Area

Pressure = F/A

Question 13

Work

Answer 13

Work = force x distance

Question 14

Work of breathing

Answer 14

The pressure volume characteristics also determine

work of breathing.

Question 15

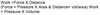
Bohr equation

Answer 15

Physiological dead space.

P_ECO₂ = mixed expired CO₂. Use P_aCO₂ for P_ACO_2.

Normally

Question 16

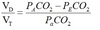
Alveolar gas equation

Answer 16

F = 2 for RA, 10 for 100%O₂

R = Resp exchange ratio

Question 17

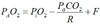
PaO2 change with age

Answer 17

Question 18

Oxygen flux

Answer 18

In dL/min

Question 19

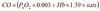
Respiratory quotient

Answer 19

Normal R= 0.8

CHO total substrate R= 1

Fat total substrate R=0.7

Question 20

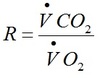
Drug concenration effect relationship

Answer 20

Question 21

The Michaelis–Menten equation

Answer 21

Michaelis–Menten equation predicts the rate of a biological reaction according
to the concentration of substrate and the specific enzyme characteristics:
See equation

where V is the velocity of reaction, Vmax is the maximum velocity of reaction, Km
is the Michaelis constant and [S] is the concentration of substrate.
The value of K
m is the substrate concentration at which V ¼ ½Vmax and is specific
to the particular reaction in question. It is the equivalent of the ED50 seen in
dose–response curves. This equation has a number of important features.
If [S] is very low, the equation approximates to

as the þ [S] term becomes negligible. This means that V is proportional to [S] by
a constant of V
max/Km. In other words the reaction is first order.
If [S] is very high the equation approximates to

and the reaction becomes zero order, as V is now independent of [S].