EM wave Flashcards
(24 cards)
Hertz discovery of radio waves (5) E + M components
- Showed waves produced when high voltage sparks jump across air gap - Showed they could be detected using a wire loop with a gap in it - EM waves spreading from the sparks created by the transmitter pass through loop and induce an emf, and a current created sparks which jumped across the detector gap - Induced alternating emf showed changing magnetic flux which is caused by wave passing through loop so wave has magnetic nature - Replacing wire loop with second dipole allows alternating electric field to be detected

How did Hertz show radio waves were transverse
- Rotating detector dipole to be perpendicular to transmitter rods caused no emf to be induced as no magnetic flux passed through it - Whereas maximum signal was obtained when parallel to dipole - Showing M+E field components of wave confined to a specific direction so EM waves were polarised and therefore transverse

Hertz stationary waves - equipment, method and how was speed determined
- Radio waves sent from transmitter to a reflector (at a distance of (n+0.5)lambda) which causes stationary waves to form - Reflector and transmitter are nodes - Detector moved between reflector and transmitter to locate two adjacent nodes - Node-to-node distance measured and then doubled to find the wavelength - Wavelength multiplied by fixed frequency to give speed of radio waves
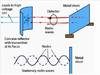
Composition of an EM wave
2 waves in phase in planes perpendicular to each other and direction of propagation/travel
The detection of the wave by the metal loop in Hertz’s experiment demonstrated the magnetic nature of the radio waves because
induced emf in the loop must be caused by changing magnetic flux through the loop. Magnetic flux change must be caused by the wave passing through the loop so the wave had a magnetic nature
Explain how the electric nature of the waves emitted by the dipole could be demonstrated
use another dipole aligned with the transmitter detects an electric field which changes
How did Hertz measure the speed of the radio wave
• diagram showing or clear description of transmitter, reflector and receiver between them. • stationary waves set up between the transmitter and reflector • interference between incident and reflected waves. • determine wavelength by measuring distance between nodes / antinodes • measured / known frequency of the radio wave • Calculate speed using v = fλ
How did Hertz’ experiments support Maxwell’s predictions
• Maxwell result developed from a prediction of e-m waves • Evidence of a substitution of data from the data booklet into the formula to give result for speed • The speed of radio waves is the same as the speed of electromagnetic waves predicted by Maxwell
Experimental evidence that suggests light is an em wave
• Fizeau determined speed of light waves • outline detail of experiment • agreement with value predicted by Maxwell suggests light waves are also electromagnetic waves
Explain why the strength of the detector signal varied repeatedly between a minimum and a maximum as the detector was moved slowly away from the transmitter along the dotted line
Reflected waves and incident waves form a stationary/standing wave pattern or interfere/reinforce/cancel (1) nodes formed where signal is a minimum
When an alternating potential difference of a suitably high frequency is applied to a transmitter, an alternating emf of the same frequency is induced in a detector loop as shown. The loop and transmitter aerial are in the same vertical plane. Explain, in terms of electromagnetic waves, why an emf is induced in the loop when in this position
magnetic wave causes alternating magnetic field (or flux) through loop (1) induced emf in loop due to changing magnetic flux (in loop) (1)
The alternating emf decreases to zero when the loop is rotated about the axis through 90° until it is horizontal. Explain why the emf is zero when the loop is horizontal
radio wave is polarised (1) no magnetic flux passes through the loop in new position
Describe, with the aid of a diagram, an electromagnetic wave propagating through free space
two waves in phase perpendicular to each other and direction of wave propagation.
Fizeau’s experiment Frequency Calculations
- Speed of light measured by passing beam of light through the gap between two cog teeth to a reflector - Cog rotated at exactly the right speed so that the reflected beam was blocked by the next cog tooth - Tooth blocked at frequency’s of f, 3f, 5f, 7f etc… as must pass the following gaps - Using the frequency of rotation and the number of gaps he could calculate the time taken for the light to travel to the reflector and back to the cog and divide the distance travelled by this to give the speed of light - Time t for wheel to turn through a distance equal to the width of one tooth, t = T/2N where N is number of teeth/gaps and T is the time of one rotation - F = 1/T so t = 1/2Nf - Light travels a distance of 2D in time t so c = 2D/t where D is the distance from the wheel to the mirror so c = 4DNf - The value obtained supported Maxwell’s claim that light was an EM wave
Maxwell’s predictions, equation explanation etc
- A disturbance in M+E fields causes a plane polarised EM wave to radiate out with vibrations of electric field and magnetic field oscillating perpendicular to each other and in the direction of propagation, in phase with each other – diagram. - That there would be a spectrum of EM waves travelling with different frequencies at the same speed in a vacuum, c (mu0e0)^-0.5 where mu0 is the permeability of free space (relates magnetic flux density to current) and e0 is the permittivity of free space (relates electric field strength to charge on object).
Show that epsilon0 has unit F/m
E=V/d = Q/ke0r^2 In units: V/m = C/e0m^2 = c/Fm So e0m^2 = Fm So e0m = F So e0 = F/m
Mu0 =
magnetic flux density per unit current per unit length
How did Maxwell’s equation prove light was an EM wave
- The constants could be measured experimentally, substituted into the equation to give 3x10^8m/s which is the speed of light so light was an EM wave.
Nth harmonic, lambda =
n/2 lambda as n antinodes e.g. 1st harmonic, stationary wave, 1/2 lambda
lambda = 2L/n
Explain the significance of Maxwell’s equation: c=(μ0ε0)-0.5 in free space
Constants μ0 and ε0 can be determined experimentally and so c can be calculated.
The value for c was 3x108m/s which equals the speed of light and so light was determined to be an electromagnetic wave
This was evidence for Huygen’s wave theory over Newton’s particle theory of light
Describe how Hertz set up a stationary wave pattern of radio waves and explain how he measured the wavelength of the radio waves from the stationary wave pattern.
Positioned a flat metal sheet several metres from the transmitter
Hertz was able to create a stationary radio wave from the superposition of the incident and reflected waves
He was then able to determine the wavelength by measuring the distance over n nodes and dividing by n-1 to give the node-to-node distance = 0.5*lambda
Hertz discovered that the strength of the radio signal from the transmitter varies according to the orientation of the detector. Explain this effect and state the conclusion.
- demonstrated polarisation
- no emf was induced upon rotating the detector dipole 90 degrees to be perpendicular to the transmitter rods
- when parallel, maximum signal was obtained
- this shows that the magnetic and electric field component of the wave is confined to a specific direction and so the radio wave is polarised
- this confirmed they were transverse because longitudinal waves cannot be polarised
In Fizeau’s experiment, the reflected light could not be observed when the cog wheel with N teeth was rotating at f Hz. Calculate the time taken for a light pulse to travel from the cog wheel to the reflector and back at this frequency
t = T/2N = 1/2Nf
Explain why light blocked at f and 3f
At frequency f, light passes through first gap is blocked upon returning by the first cog then the next occasion this would happen is when light passes through the first gap is getting blocked by the seconf cog, which means it must not reach the second gap. The light reaches the next gap/cog at 2f, 3f, 4f etc and so the light would be blocked by a cog at f, 3f, 5f, 7f and pass through a gap at 2f, 4f, 6f, etic
Therefore light blocked at f, 3f, 5f, 7f, (2n+1)f for all positive integers n



