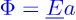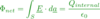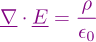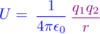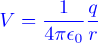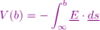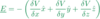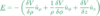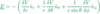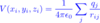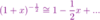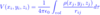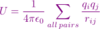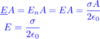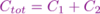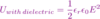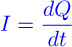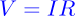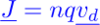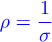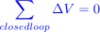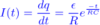Electricity Flashcards
Basic info about the electron
Charge: -1.602x10-19. Smallest possible chunk of charge. Cannot be split.
Basic info about charge
Net charge is conserved. Units: coulombs (C)
Coulomb’s law
Understand how polarisation can be induced
Electron clouds are shifted slightly by an external charge. Or free electrons are shifted (in a conductor)
An understanding of electron orbitals including a)size of Hydrogen, b)relative size of shell, c)orbital shape d)why electrons are in set orbitals
a) Hydrogen is approx 100 pm diameter, b)if the nucleus is enlarged to a golf ball the first shell is approx 1km away, c) shape depends on orbital and orbitals don’t have edges d) electrons form standing waves around the nucleus
An understanding of comparative strengths of electrostatic force and gravity
It takes a balloon (with a few billion electrons) to induce a charge on a small piece of paper and counteract the pull of the whole earth
Electric field equation
Electric field units
NC-1
How to convert between F and E
F12=q1E
Electric field in words
Electric force per positive unit charge at a point (or the force a charge WOULD feel if it were there)
Three rules for electric field lines
1) They point in the direction a positive charge would go, 2) in systems with a net charge of 0 all field lines begin on a positive charge and end on a negative charge, 3) the number of field lines per unit area through a surface perpendicular to the field lines is proportional to the magnitude of the field in that region
What is permittivity in words?
How easy it is for the electron clouds in a material to absorb energy (or ‘resistance to forming an electric field’)
How do you get the total permittivity?
What is the difference bewteen relative susceptibility and permittivity?
They are almost the same: relative susceptibility + 1 = permittivity
What effect does high permittivity have on the force or electric field?
High permittivity (means a lot of energy will be used shifting electrons) results in a smaller force or electric field
To understand how to find electric field at a point from multiple charges
Simply add the electric field from each charge together
To understand how to find the electric field from a continuous charge
Split volume into tiny sections dV. Add up the total charge from all of these in an integration
Charge from a volume dV
dq=ρ dV (where ρ is the charge density in the volume)
To understand the difference between summation and integration
When we split a volume, area or line into smaller sections then integration must be used to make sure we add up all the dVs. When finding the total charge it is not necessary to split into dVs when the charge density is constant throughout - then we can just multiply ρ and V. But if finding the electric field y(with constant density) you would still have to integrate as each section dq is a different distance from the point.
Give equation for dot product and explain where this comes from
|a||b|cosθ Put the two vectors base to base so one is along the x axis and find the lengths of the x and y components of each. Then multiply the two x components and add that to the multiple of the two y components.
What does ‘flux’ mean in general?
The total amount of SOMETHING passing through an area
What is electric flux in words?
It corresponds to the total number of field lines penetrating a surface
In terms of field lines, what is the difference btween electric field and flux?
Electric field is proportional to the number of field lines per unit area, whereas flux is proportional to the total number of field lines
Give an equation relating flux and electric field (for a surface perpendicular to E)
Understand why the flux/electric field equation needs to be modified when the area is not perpendicular
If the area is not perpendicular to E then it will give a smaller reading for Φ than it should
Give an equation relating flux and electric field (for a surface NOT perpendicular to E)
Be able to derive Gauss’s law from Cloumb’s law for a point charge
Be able to derive Gauss’s law from Coulomb’s law for a point charge contained within a non-symmetrical surface
The same as for a point charge, since the non-symmetrical surface can be replaced with a sphere for the purposes of calculating the net flux - as the net flux through both is the same (the area from the ‘E’ and from the ‘da’ cancel)
To understand why Gauss’s law has ‘Q_internal’ (sometimes written ‘Q_total’) rather than just Q
When multiple charges are contained within the surface the principle of superposition can be used to show that ‘Q’ becomes ‘Q_internal’. This is then used as the more generalised formula.
To remember Gauss’s law
To explain why Gauss’s law is valid for all surfaces and charge distributions
Because the NET flux is not affected by where the charges are or what shape surface you use.
To explain why Gauss’s law is independent of the distance from the charge we draw the Gaussian surface
The NET flux through the surface is not affected by the distance from the surface.
To understand why there is no electric field in a hollow space inside a conductor
There is no charge in a hollow space - hence (due to Gauss’s law) no net field inside
To be able to use Gauss’s law to find the electric field inside and outside a charged solid sphere
For outside the sphere, same as a point charge. Same derivation as Gauss’ law from coulomb but dont sub in E.
For inside the sphere, set RHS of Gauss’ eq. to charge density x volume. LHS is E x surface area. Equate and solve for E.
To be able to use Gauss’s law to find the electric field inside and outside a charged hollow sphere
Inside is just zero as RHS of Gauss’ is zero.
Outside is just a point charge
To be able to use Gauss’s law to find the electric field a distance from a charged line
Using cylinder as charge radiating radially.
Top and bottom are zero as parallel to E.
LHS of Gauss’ becomes Eda=E 2Pi r l.
RHS=Q/epsilon=lambda x length/…
To be able to use Gauss’s law to find the electric field a distance from a charged plane
Cylinder byt opposite of line charge
To understand when we need the differential form of Gauss’s law
When the electric field is not constant at all points on the Gaussian surface and it is not possible to take the ‘E’ to the front of the integral in Gauss’s law
To be able to follow the derivation of the differential form of Gauss’s law
See lecture notes
To remember the differential form of Gauss’s law
To be able to describe divergence in words
If there is more stuff (could be particles, electric field lines etc.) leaving an area than is going in, the that area is acting as a source and the divergence is positive. If there is more stuff going in than leaving then the area is acting as a sink and there is convergence (or negative divergence).
To be able to take the divergence of a function eg.
To know the equation for electric potential energy
To know the equation for electric potential
To know how to go about finding the equation for potential energy in words
To find the work done (energy) in bringing a charge close to another charge
To be able to show how potential relates to electric field ie.
Start by finding the work done to bring two charges together - see lecture notes.
To know an equation for electric force using Grad
To know an equation for electric field using Grad
To know the Grad equation for E in cartesian co-ordinates
To know the Grad equation for E in cylindrical co-ordinates
To know the Grad equation for E in speherical co-ordinates
To be able to find the potential of several point charges
To understand what an electric dipole is in words
Equal but opposite separated charges. Overall charge on a molecule is zero, but the more electronegative atom pulls electrons towards itself more than the others resulting in a slight net movement of electrons to this side of the molecule.
To know what electric dipole moment is and an equation for it
A measure of how much the electrons have shifted over in a dipole. p=2qd (where 2d is the separation of the charges)
To know which direction the dipole moment points
In the direction the POSITIVE charges go
To understand the difference between permanent and induced electric dipole
If a moelcule has an electric dipole in the absence of external electric field, it has a permanent electric dipole. Dipoles can also in some molecules be induced by an external electric field (or this can increase a dipole that was already there)
To understand how induced dipoles relate to polarisability and suceptibility
Polarisability (or susceptibility) describes how easy it is to push electrons to one side in a molecule and create a dipole.
To be able to derive the electric potential for a dipole
To know the binomial expansion equation and how to use it
To know how to find the electric potential for a continuous charge distribution
To know how to find the electric potential energy for a group of discrete charges
Find the energy to bring each new charge towards EACH of the others and sum:
Know how to go about finding the potential energy of a continuous charge distribution
- Consider sphere of radius a, imagine building up sphere layer by layer.
- Get potential for partial built sphere.
- dU=dq Qr. Calculate dq and Qr. Sub in.
- Integrate dU w/ respect to r, between a and 0.
- Sub back in Q
To be able to explain why there is no NET electric field inside a conductor in equilibrium
In a conductor at equilibrium the charges are stationary, therefore there is no net force acting on them, therefore there is no electric field
To be able to explain why in a conductor at equilibrium all charge must be on the surface
Gauss’s law tells us that if there is no net electric field inside, then there is no net charge inside. Therefore all charge must be on the surface.
To know which direction the electric field points at the surface of a conductor (and be able to explain why)
It points directly outwards ie. Is perfectly perpendicular to the surface (if there was a sideways component the charges would move until this disappeared)
Know how to figure out the electric field from an infinite plane using Gauss’s law
To know what happens when you bring two oppositely charged conducting plates together
The charges gradually move to the inside surfaces and as they do so the electric field on the outside goes to zero, while the field between the plates doubles.
Understand the concept of ‘method of images’ and why it is used
Some parts of the system eg. Infinite charged plates are replaced with single imaginary charges (making sure the result has the same boundary conditions). It is used to find the electric fields in some conplicated situations such as outside conductors
To know what a capacitor is in words
Two conductors with equal charges which have opposite signs
To know the electric field between capacitor plates
(ignoring edge effects)
To be able to explain what the potential difference between capacitor plates really means
It is the difference in energy (per charge) that a charge WOULD have if it were on one plate rather than the other plate
To be able to work out the potential energy to move a charge (q2) from one plate to the other
Know how to find an equations for the charge stored by a capacitor
Divide potential energy by charge to get potential, then rearrange that to get q
Know an equation for capacitance involving Area and separation of the plates
C=ε_0 A /d
Know the units of capacitance
farads, F
To know what makes for larger capacitance in a capacitor
Larger area, smaller separation
Know an equation frelating capacitance to potential difference
Know the difference between a battery and a capacitor
Batteries produce electrons at one terminal by and remove at the other via chemical reactions. Capacitors don’t make electrons only store them.
Know how to find the capacitance of a spherical capacitor
- Imagine two concentric shells, inner with radius a and outer with radius b.
- Outside of b, v=0. At r=b, v=(point charge). At r=a, v=(point chrage).
- Change in potential = va-vb.
- Q=cv, rearrange, sub-in.
Know how to find the capacitance of single sphere
b tends towards infinite
Know how to find the capacitance of a cylindrical capacitor
- If L is much larger than b, we neglect end effects are use E for infinite line.
- Outside cylinder, field is that due to to a line of charge.
- Sub lambda=Q/L into E for infinte line.
- Integrate between outer and inner cylinders (bewteen b and a) to get change in V
- Sub into Q=VC
Know the equation for adding capacitors in series (and how to derive that equation)
Know the equation for adding capacitors in parallel (and how to derive that equation)
Know the energy stored in a capacitor, and why there is a 1/2 in the equation
or
Know how to go about finding the energy density of a capacitor
energy density is the total energy stored divided by the volume between the plates
To be able to say what a polar molecule is in words
They are molecules with a permanent dipole moment even without an external field
Be able to give an example of a polar and non-polar moelcule
eg. HF is polar, H_2 is non-polar (ie. Symmetrical)
Know the meaning of ‘electronegative’
the more electronegative side of a molecule is more ‘electron-grabbing’
Know how ‘polarisation’ is defined (in equation form)
Know an equation relating polarisation to external electric field (for molecules with no permanent electric dipole moment)
To know three examples of relative permittivity values
eg. Vacuum:1, paper: ~4, acid: ~80
Know what a ‘dielectric’ is
an insulator
To know what happens to the molecules in a dielectric when you apply an external field when a) it had no permanent dipole moment and b) it had a permanent dipole moment
a) dipole moments are induced by the external field, b) molecules will spin (if they can) to align with the external field. The external field may alos induce more of a dipole than they had originally
Know what happens to capacitance of a capacitor when you insert a dielectric and why
potential difference is decreased as it is partly cancelled out by molecules in the dielectric, resulting in INCREASED capacitance
To be able to explain what exactly happens when you charge up a capacitor, then disconnect the battery, then insert a dielectric
inserting the dielectric reduces the potential difference, which increases capacitance:
To be able to explain what exactly happens when you charge up a capacitor, then insert a dielectric (leaving battery connected)
Inserting the dielectric reduces the potential difference, which the battery then increases back to the value on the battery by increasing the charge held on each plate. Then as V is the same but Q is increased, C is increased:
To know how capacitance with dielectric relates to capacitance without dielectric
To understand what type of dielectric will increase the capacitance more
The more ‘susceptible’ the molecules are to polarisation, the stronger the ‘cancelling’ effect of the dielectric will be
To know how the energy of a capacitor differs with insertion of a dielectric
relative permittivity is included:
Know how to derive an equation for the torque on an electric dipole in an external field
Know how to derive the potential energy of a dipole in an external field
Know which way electrons and current flow in a circuit
electrons flow -ve to +ve battery terminals, ‘current’ flows in the opposite direction
Know what happens when you add a resistor to a circuit
The resistor contains a material that the electrons ‘bump into’ a lot, slowing them down. All electrons in the circuit travel at this new lower speed.
To be able to define ‘current’ in words
The amount of charge that is flowing through a cross section of the circuit per second
To know the equation for current
To know ohm’s law
(the current that flows is proportional to the potential difference)
To know the difference between conductors and insulators
conductors have an electron that will move with very little electric force from the battery so can dissociate itself from its atom and move on to the next one – it is basically free. Insulators hold on tight to their outer electrons, but if you turn up the potential difference of the battery enough you can get insulators to conduct also (eg. lightning). Semiconductors usually act like insulators but we can make them act like conductors under certain conditions.
To know an equation for current density in terms of number of charge carriers and drift velocity
To know how to get the current from the current density
To know how resistances add in series
To know how to derive how resistances add in series
To know how resistances add in parallel
To know how to derive how resistances add in parallel
To be able to figure out the equivalent resistance or capacitance of a complex circuit
Work in steps, finding the equivalent resistance/capacitance of 2 or more resistors and simplifying
To understand why resistance is constant in an OHMIC material
As resistance =V/I and we want to increase the resistance can we increase V and keep current the same? No – if we increase V the current will increase. In order to change R we need to change the resistor itself
Know the equation describing how physical factors affect resistance
Know how resistivity relates to conductivity
Know an equation relating current density to electric field
Know how to derive an equation for the power lost over a reduction in voltage
Know units for power
watt (W) or Js-1
Know where the energy goes when a charge drops through a change in voltage in a resistor
As the charge bumps into molecules in the resistor, it transfers energy and the resistor heats up
To be able to describe what ‘EMF’ is in words
The work done to move charges from one side to the other in a battery against the potential gradient
know the equation for EMF
Know Kirchoff’s loop rule in words and equation form
Including the battery there is no net voltage change in a closed loop
Know Kirchoff’s junction rule in words and equation form
The sum of current entering any junction must equal the sum of current leaving it
To be able to derive an equation for how current in a capacitor varies with time as the capacitor is charged up
See lecture notes for derivation
