EIT/FE Math 1

Question 1

Exponeant Manipulations:

x^-a

x^ax^b

(xy)^a

x^ab

Answer 1

Exponeant Manipulations:

1/x^a

x^a+b

x^ay^a

(x^a)^b

Question 2

ln x^a

ln(xy)

ln(x/y)

lnx

log_bb

ln(1)

ln(e^a)

ln_ay

Answer 2

a*ln(x)

ln(x) + ln(y)

ln(x) - ln(y)

e*log(x)

1

0

a

implies a^x = y

Question 3

Right Triangles only

sin²θ + cos²θ = 1

sin2θ

cos2θ

sin(a+/-b)

cos(a+/-b)

Answer 3

1

2sinθ cosθ

2cos²θ - sin²θ

sin(a)*cos(b)+/-sin(b)cos(a)

cos(a)*cos(b)+/-sin(a)sin(b)

Question 4

Law of Sines

Use to calculate unknown angles/lines using 3 knowns

Answer 4

a sin A = b sin B = c sin C

Question 5

Law of Cosines

Answer 5

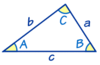
c2 = a2 + b2 − 2ab cos(C)

Question 6

Equation of a straight line: Ax=By+C=0

point-slope

slope intercept

two intercept

Answer 6

point-slope; y-y1 = m (x-x1)

slope intercept; y = m(x-x1)

two intercept; x/a + y/b =1

Question 7

Areas of common shapes

Question 8

Volum of Common Solids

Question 9

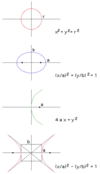
Conic Sections

General Equation Ax² + 2Bxy + Cy² + 2 Dx +Ey +F=0

Ellipse;

Parabola;

Hyperbola;

Answer 9

Ellipse; B²- AC < 0 (circle if B=0 , A=C)

Parabola; B2- AC = 0

Hyperbola; B2- AC > 0

Question 10

Conic Section Equations

Question 11

Polar Coordinate equations

Answer 11

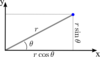
x = r cos(θ),
y = r sin(θ)

Question 12

Cylindrical Coordinate Equations

Answer 12

x = r cos(θ),
y = r sin(θ)

z=z

Question 13

Cylindrical Coordinate Equations

Answer 13

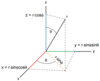
x = r sin(ϕ)cos(θ),
y = r sin(ϕ)sin(θ),

z= r cos(ϕ)

Question 14

i = sqroot (-1)

Euler Formula

Complex Number Identity

Answer 14

e^iθ=cosθ+ isinθ

e^iθ=e^i(θ+2nπ)

Question 15

Add complex and real numbers sepparatly

(a+bi) + (c+di) = (a+c) + (b+d)i

Answer 15

ie

(3 + 2i) + (1 + 7i) = (4 + 9i)

Question 16

Use Binomial Multiplication (foil)

(a+bi)(c+di) = ac + adi + bci + bdi2

Firsts: a × c

Outers: a × di

Inners: bi × c

Lasts: bi × di

Answer 16

Example

(3 + 2i)(1 + 7i)

(3 + 2i)(1 + 7i) = 3×1 + 3×7i + 2i×1+ 2i×7i

= 3 + 21i + 2i + 14i2

= 3 + 21i + 2i - 14(because i2 = -1)

= -11 + 23i

Question 17

Definitions;

Derivative

Integral

Limit

Question 18

Derivative formulas where f and g are functions of x and k

dk/dx

d(kxⁿ)/dx

d/dx(f+g)

dfⁿ/dx

d/dx(fg)

Answer 18

dk/dx = 0

d(kxⁿ)/dx = knx^n-1

d/dx(f+g) = f ‘ + g ‘

dfⁿ/dx = nf ^n-1 f ‘

d/dx(fg) = fg ‘ +gf ‘

Question 19

Derivative formulas where f and g are functions of x and k is constant

d/dx (ln x)

d/dx (e^kx)

d/dx (sin x)

d/dx (cos x)

Answer 19

d/dx (ln x) = 1/x

d/dx (e^kx) = ke^kx

d/dx (sin x) = cos x

d/dx (cos x) = -sin x

Question 20

L’Hospitals Rule

Answer 20

Question 21

Taylor Series

Answer 21

Question 22

Scalor Vector Multiplication aka dot product

A*B =

Answer 22

A*B = A B cos θ

Question 23

Permutations

P(n , r)

Combinations

C (n , r)

Answer 23

P(n , r) = n!/(n-r)!

C(n , r) = n!/r!(n-r)!

Question 24

Permutations

P(A or B)

P(A and B)

P(not A)

P(A or B)

Answer 24

P(A or B) = P(A) + P(B)

P(A and B) = P(A) * P(B)

P(not A) = 1 - P(A)

P(A or B) = P(A) + P(B) - P(A)P(B)