DS interview questions Flashcards
Source: https://www.edureka.co/blog/interview-questions/data-science-interview-questions/ https://towardsdatascience.com/over-100-data-scientist-interview-questions-and-answers-c5a66186769a
50 small DT vs 1 big one
“Is a random forest a better model than a decision tree?”
- yes because a random forest is an ensemble method that takes many weak decision trees to make a strong learner.
- more accurate, more robust, and less prone to overfitting.
Administrative datasets vs Experimental studies datasets.
Administrative datasets are typically
- datasets used by governments or other organizations for non-statistical reasons.
- Usually larger and more cost-efficient than experimental studies.
- Regularly updated assuming that the organization associated with the administrative dataset is active and functioning.
- May not capture all of the data that one may want and may not be in the desired format either.
- It is also prone to quality issues and missing entries.
What is A/B testing?
A/B testing is a form of hypothesis testing and two-sample hypothesis testing to compare two versions, the control and variant, of a single variable. It is commonly used to improve and optimize user experience and marketing.
Analyze a Data
Exploratory Data Analysis to clean, explore, and understand my data.
Compose a histogram of the duration of calls to see the underlying distribution.
What is bias-variance trade-off?
Bias: Bias is an error introduced in your model due to oversimplification of the machine learning algorithm. It can lead to underfitting. When you train your model at that time model makes simplified assumptions to make the target function easier to understand.
- Low bias machine learning algorithms — Decision Trees, k-NN and SVM
- High bias machine learning algorithms — Linear Regression, Logistic Regression
Variance: Variance is error introduced in your model due to complex machine learning algorithm, your model learns noise also from the training data set and performs badly on test data set. It can lead to high sensitivity and overfitting.
Normally, as you increase the complexity of your model, you will see a reduction in error due to lower bias in the model. However, this only happens until a particular point. As you continue to make your model more complex, you end up over-fitting your model and hence your model will start suffering from high variance.
Bias-Variance trade-off: The goal of any supervised machine learning algorithm is to have low bias and low variance to achieve good prediction performance.
- The k-nearest neighbour algorithm has low bias and high variance, but the trade-off can be changed by increasing the value of k which increases the number of neighbours that contribute to the prediction and in turn increases the bias of the model.
- The support vector machine algorithm has low bias and high variance, but the trade-off can be changed by increasing the C parameter that influences the number of violations of the margin allowed in the training data which increases the bias but decreases the variance.
There is no escaping the relationship between bias and variance in machine learning. Increasing the bias will decrease the variance. Increasing the variance will decrease bias.
How do you control for biases?
Two common things include randomization, where participants are assigned by chance, and random sampling, sampling in which each member has an equal probability of being chosen.
When you sample, what bias are you inflicting?
- Sampling bias: a biased sample caused by non-random sampling
- Under coverage bias: sampling too few observations
- Survivorship bias: error of overlooking observations that did not make it past a form of selection process.
- Selection Bias - sample obtained is not representative of the population intended to be analysed.
Unbalanced Binary Classification
- First, you want to reconsider the metrics that you’d use to evaluate your model. The accuracy of your model might not be the best metric to look at because and I’ll use an example to explain why. Let’s say 99 bank withdrawals were not fraudulent and 1 withdrawal was. If your model simply classified every instance as “not fraudulent”, it would have an accuracy of 99%! Therefore, you may want to consider using metrics like precision and recall.
- Another method to improve unbalanced binary classification is by increasing the cost of misclassifying the minority class. By increasing the penalty of such, the model should classify the minority class more accurately.
- Lastly, you can improve the balance of classes by oversampling the minority class or by undersampling the majority class.
Boosting
Boosting is an ensemble method to improve a model by reducing its bias and variance, ultimately converting weak learners to strong learners.
The general idea is to train a weak learner and sequentially iterate and improve the model by learning from the previous learner.
- AdaBoost - adds weight and bias to weaker learners
- Gradient Boosting - retrained loss
- XGBoost - better/faster Gradient boosting using parallel models
Boxplot vs Histogram
Boxplots and Histograms are visualizations used to show the distribution of the data
Histograms - bar charts
- show the frequency of a numerical variable’s values and are used to approximate the probability distribution of the given variable.
- It allows you to quickly understand the shape of the distribution, the variation, and potential outliers.
Boxplots
- you can gather other information like the quartiles, the range, and outliers.
- useful when you want to compare multiple charts at the same time because they take up less space than histograms.
Central Limit Theorem
CLT - sampling distribution of the sample mean approaches a normal distribution as the sample size gets larger no matter what the shape of the population distribution.
The central limit theorem is important because it is used in hypothesis testing and also to calculate confidence intervals.
What is Cluster Sampling?
Cluster sampling is a technique used when it becomes difficult to study the target population spread across a wide area and simple random sampling cannot be applied. Cluster Sample is a probability sample where each sampling unit is a collection or cluster of elements.
For eg., A researcher wants to survey the academic performance of high school students in Japan. He can divide the entire population of Japan into different clusters (cities). Then the researcher selects a number of clusters depending on his research through simple or systematic random sampling.
Collinearity / Multi-collinearity
Multicollinearity exists when an independent variable is highly correlated with another independent variable in a multiple regression equation. This can be problematic because it undermines the statistical significance of an independent variable.
You could use the Variance Inflation Factors (VIF) to determine if there is any multicollinearity between independent variables — a standard benchmark is that if the VIF is greater than 5 then multicollinearity exists.
In a study of emergency room waiting times, investigators consider a new and the standard triage systems. To test the systems, administrators selected 20 nights and randomly assigned the new triage system to be used on 10 nights and the standard system on the remaining 10 nights. They calculated the nightly median waiting time (MWT) to see a physician. The average MWT for the new system was 3 hours with a variance of 0.60 while the average MWT for the old system was 5 hours with a variance of 0.68. Consider the 95% confidence interval estimate for the differences of the mean MWT associated with the new system. Assume a constant variance. What is the interval? Subtract in this order (New System — Old System).
https://miro.medium.com/max/776/0*QpSg349Ozhe-etIQ.png
Confidence Interval = mean +/- t-score * standard error (see above)
mean = new mean — old mean = 3–5 = -2
t-score = 2.101 given df=18 (20–2) and confidence interval of 95%
standard error = sqrt((0.⁶²*9+0.⁶⁸²*9)/(10+10–2)) * sqrt(1/10+1/10)
standard error = 0.352
confidence interval = [-2.75, -1.25]
To further test the hospital triage system, administrators selected 200 nights and randomly assigned a new triage system to be used on 100 nights and a standard system on the remaining 100 nights. They calculated the nightly median waiting time (MWT) to see a physician. The average MWT for the new system was 4 hours with a standard deviation of 0.5 hours while the average MWT for the old system was 6 hours with a standard deviation of 2 hours. Consider the hypothesis of a decrease in the mean MWT associated with the new treatment. What does the 95% independent group confidence interval with unequal variances suggest vis a vis this hypothesis? (Because there’s so many observations per group, just use the Z quantile instead of the T.)
Assuming we subtract in this order (New System — Old System):
confidence interval formula for two independent samples
mean = new mean — old mean = 4–6 = -2
z-score = 1.96 confidence interval of 95%
st. error = sqrt((0.⁵²*99+²²*99)/(100+100–2)) * sqrt(1/100+1/100)
standard error = 0.205061
lower bound = -2–1.96*0.205061 = -2.40192
upper bound = -2+1.96*0.205061 = -1.59808
confidence interval = [-2.40192, -1.59808]
You are running for office and your pollster polled hundred people. Sixty of them claimed they will vote for you. Can you relax?
- Assume that there’s only you and one other opponent.
- Also, assume that we want a 95% confidence interval. This gives us a z-score of 1.96.
p-hat = 60/100 = 0.6
z* = 1.96
n = 100
This gives us a confidence interval of [50.4,69.6]. Therefore, given a confidence interval of 95%, if you are okay with the worst scenario of tying then you can relax. Otherwise, you cannot relax until you got 61 out of 100 to claim yes.
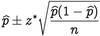
In a population of interest, a sample of 9 men yielded a sample average brain volume of 1,100cc and a standard deviation of 30cc. What is a 95% Student’s T confidence interval for the mean brain volume in this new population?
Given a confidence level of 95% and degrees of freedom equal to 8, the t-score = 2.306
Confidence interval = 1100 +/- 2.306*(30/3)
Confidence interval = [1076.94, 1123.06]
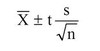
A diet pill is given to 9 subjects over six weeks. The average difference in weight (follow up — baseline) is -2 pounds. What would the standard deviation of the difference in weight have to be for the upper endpoint of the 95% T confidence interval to touch 0?
Upper bound = mean + t-score*(standard deviation/sqrt(sample size))
0 = -2 + 2.306*(s/3)
2 = 2.306 * s / 3
s = 2.601903
Therefore the standard deviation would have to be at least approximately 2.60 for the upper bound of the 95% T confidence interval to touch 0.
What is the difference between Point Estimates and Confidence Interval?
Point Estimation gives us a particular value as an estimate of a population parameter. Method of Moments and Maximum Likelihood estimator methods are used to derive Point Estimators for population parameters.
A confidence interval gives us a range of values which is likely to contain the population parameter. The confidence interval is generally preferred, as it tells us how likely this interval is to contain the population parameter. This likeliness or probability is called Confidence Level or Confidence coefficient and represented by 1 — alpha, where alpha is the level of significance.
What are confounding variables?
A confounding variable, or a confounder, is
- a variable that influences both the dependent variable and the independent variable, causing a spurious association,
- a mathematical relationship in which two or more variables are associated but not causally related.
What is a confusion matrix?
The confusion matrix is a 2X2 table that contains 4 outputs provided by the binary classifier. Various measures, such as error-rate, accuracy, specificity, sensitivity, precision and recall are derived from it.
A binary classifier predicts all data instances of a test data set as either positive or negative. This produces four outcomes:
- True-positive(TP) — Correct positive prediction
- False-positive(FP) — Incorrect positive prediction
- True-negative(TN) — Correct negative prediction
- False-negative(FN) — Incorrect negative prediction
Basic measures derived from the confusion matrix
- Error Rate = (FP+FN)/(P+N)
- Accuracy = (TP+TN)/(P+N)
- Sensitivity(Recall or True positive rate) = TP/P = TP/(TP+FN)
- Specificity(True negative rate) = TN/N = TN/(TN+FP)
- Precision(Positive predicted value) = TP/(TP+FP)
- F-Score(Harmonic mean of precision and recall) = (1+b)(PREC.REC)/(b²PREC+REC) where b is commonly 0.5, 1, 2.
F1-Score = (2 * Precision * Recall) / (Precision + Recall)
Convex vs Non-Convex cost function
A convex function is one where a line drawn between any two points on the graph lies on or above the graph. It has one minimum.
A non-convex function is one where a line drawn between any two points on the graph may intersect other points on the graph. It characterized as “wavy”.
When a cost function is non-convex, it means that there’s a likelihood that the function may find local minima instead of the global minimum, which is typically undesired in machine learning models from an optimization perspective.
What is correlation and covariance in statistics?
Both Correlation and Covariance establish the relationship and also measure the dependency between two random variables.
Correlation: Correlation is considered or described as the best technique for measuring and also for estimating the quantitative relationship between two variables. Correlation measures how strongly two variables are related.
Covariance: In covariance two items vary together and it’s a measure that indicates the extent to which two random variables change in cycle. It is a statistical term; it explains the systematic relation between a pair of random variables, wherein changes in one variable reciprocal by a corresponding change in another variable.
Cross-Validation
Cross-validation is essentially a technique used to assess how well a model performs on a new independent dataset. The simplest example of cross-validation is when you split your data into two groups: training data and testing data, where you use the training data to build the model and the testing data to test the model.
The goal of cross-validation is to limit problems like overfitting and get an insight on how the model will generalize to an independent data set.
How does data cleaning plays a vital role in the analysis?
Data cleaning can help in analysis because:
- Cleaning data from multiple sources helps to transform it into a format that data analysts or data scientists can work with.
- Data Cleaning helps to increase the accuracy of the model in machine learning.
- It is a cumbersome process because as the number of data sources increases, the time taken to clean the data increases exponentially due to the number of sources and the volume of data generated by these sources.
- It might take up to 80% of the time for just cleaning data making it a critical part of the analysis task.
Data Wrangling / Cleaning
- Data profiling: Almost everyone starts off by getting an understanding of their dataset. More specifically, you can look at the shape of the dataset with .shape and a description of your numerical variables with .describe().
- Data visualizations: Sometimes, it’s useful to visualize your data with histograms, boxplots, and scatterplots to better understand the relationships between variables and also to identify potential outliers.
- Syntax error: This includes making sure there’s no white space, making sure letter casing is consistent, and checking for typos. You can check for typos by using .unique() or by using bar graphs.
- Standardization or normalization: Depending on the dataset your working with and the machine learning method you decide to use, it may be useful to standardize or normalize your data so that different scales of different variables don’t negatively impact the performance of your model.
- Handling null values: There are a number of ways to handle null values including deleting rows with null values altogether, replacing null values with the mean/median/mode, replacing null values with a new category (eg. unknown), predicting the values, or using machine learning models that can deal with null values. Read more here.
- Other things include: removing irrelevant data, removing duplicates, and type conversion.
Decision Tree
Decision trees
- popular model, used in operations research, strategic planning, and machine learning.
- Each square above is called a node, and the more nodes you have, the more accurate your decision tree will be (generally). The last nodes of the decision tree, where a decision is made, are called the leaves of the tree.
- Decision trees are intuitive and easy to build but fall short when it comes to accuracy.
Dimension Reduction
Dimensionality reduction is the process of reducing the number of features in a dataset. This is important mainly in the case when you want to reduce variance in your model (overfitting).
Four advantages of dimensionality reduction:
- It reduces the time and storage space required
- Removal of multi-collinearity improves the interpretation of the parameters of the machine learning model
- It becomes easier to visualize the data when reduced to very low dimensions such as 2D or 3D
- It avoids the curse of dimensionality
Dimensionality Reduction before fitting
When the number of features is greater than the number of observations, then performing dimensionality reduction will generally improve the SVM.
What are Eigenvectors and Eigenvalues?
Eigenvectors are used for understanding linear transformations. In data analysis, we usually calculate the eigenvectors for a correlation or covariance matrix. Eigenvectors are the directions along which a particular linear transformation acts by flipping, compressing or stretching.
Eigenvalue can be referred to as the strength of the transformation in the direction of eigenvector or the factor by which the compression occurs.
Experimental data vs Observational data
Observational data comes from observational studies which are when you observe certain variables and try to determine if there is any correlation.
Experimental data comes from experimental studies which are when you control certain variables and hold them constant to determine if there is any causality.
- An example of experimental design is the following: split a group up into two. The control group lives their lives normally. The test group is told to drink a glass of wine every night for 30 days. Then research can be conducted to see how wine affects sleep.
False Positive vs False Negative
False positive is an incorrect identification of the presence of a condition when it’s absent.
- predict positive when actual value is negative
- spam dectection
False negative is an incorrect identification of the absence of a condition when it’s actually present.
- predict negative when actual value is positive
- screening for cancer.
This is a subjective argument, but false positives can be worse than false negatives from a psychological point of view. For example, a false positive for winning the lottery could be a worse outcome than a false negative because people normally don’t expect to win the lottery anyways.
Suppose that diastolic blood pressures (DBPs) for men aged 35–44 are normally distributed with a mean of 80 (mm Hg) and a standard deviation of 10. About what is the probability that a random 35–44 year old has a DBP less than 70?
Since 70 is one standard deviation below the mean, take the area of the Gaussian distribution to the left of one standard deviation.
= 2.3 + 13.6 = 15.9%
How do you prove that males are on average taller than females by knowing just gender height?
- Null hypothesis: males and females are the same height on average
- Alternative hypothesis: the average height of males is greater than the average height of females.
- Collect random sample of heights of males and females and
- Use a t-test to determine if you reject the null or not.
Kernel
- A kernel is a way of computing the dot product of two vectors 𝐱x and 𝐲y in some (possibly very high dimensional) feature space, which is why kernel functions are sometimes called “generalized dot product” [2]
- The kernel trick is a method of using a linear classifier to solve a non-linear problem by transforming linearly inseparable data to linearly separable ones in a higher dimension.
What is the Law of Large Numbers?
The Law of Large Numbers is a theory that states that as the number of trials increases, the average of the result will become closer to the expected value.
It says that the sample means, the sample variance and the sample standard deviation converge to what they are trying to estimate.
Eg. flipping heads from fair coin 100,000 times should be closer to 0.5 than 100 times.
What is: lift, KPI, robustness, model fitting, design of experiments, 80/20 rule?
Lift: lift is a measure of the performance of a targeting model measured against a random choice targeting model; in other words, lift tells you how much better your model is at predicting things than if you had no model.
KPI: stands for Key Performance Indicator, which is a measurable metric used to determine how well a company is achieving its business objectives. Eg. error rate.
Robustness: generally robustness refers to a system’s ability to handle variability and remain effective.
Model fitting: refers to how well a model fits a set of observations.
Design of experiments: also known as DOE, it is the design of any task that aims to describe and explain the variation of information under conditions that are hypothesized to reflect the variable. [4] In essence, an experiment aims to predict an outcome based on a change in one or more inputs (independent variables).
80/20 rule: also known as the Pareto principle; states that 80% of the effects come from 20% of the causes. Eg. 80% of sales come from 20% of customers.
20
Linear Model
Linear Model assumptions:
- Linear relationship - relationship between the independent and dependent variables to be linear. The linearity assumption can best be tested with scatter plots, and a regression line.
- Multivariate normality - data (all variables) normally distributed, bell curve test with Histogram plot
-
No or little multicollinearity - Multicollinearity occurs when the independent variables are too highly correlated with each other. Simplest way to address the problem is to remove independent variables with high VIF values.
Multicollinearity may be tested with three central criteria:- Correlation matrix - Pearson’s Bivariate Correlation
- Tolerance - measures the influence of one independent variable on all other independent variables; the tolerance is calculated with an initial linear regression analysis.
- Variance Inflation Factor (VIF) - With VIF > 5 there is an indication that multicollinearity may be present; with VIF > 10 there is certainly multicollinearity among the variables.
- No auto-correlation - Autocorrelation occurs when the residuals are not independent from each other. Durbin-Watson test for auto-correlation.
- Homoscedasticity - The scatter plot is good way to check whether the data are homoscedastic (meaning the residuals are equal across the regression line).
17
Linear Regression assumptions
Same as Linear Model assumptions:
- The sample data used to fit the model is representative of the population
- The relationship between X and the mean of Y is linear
- The variance of the residual is the same for any value of X (homoscedasticity)
- Observations are independent of each other
- For any value of X, Y is normally distributed.
- Extreme violations* of these assumptions will make the results redundant.
- Small violations* of these assumptions will result in a greater bias or variance of the estimate.
What is the difference between “long” and “wide” format data?
- In the wide-format, a subject’s repeated responses will be in a single row, and each response is in a separate column.
- In the long-format, each row is a one-time point per subject. You can recognize data in wide format by the fact that columns generally represent groups.
Long-tailed Distribution
A long-tailed distribution is a type of heavy-tailed distribution that has a tail (or tails) that drop off gradually and asymptotically.
It’s important to be mindful of long-tailed distributions in classification and regression problems because the least frequently occurring values make up the majority of the population. This can ultimately change the way that you deal with outliers, and it also conflicts with some machine learning techniques with the assumption that the data is normally distributed.
3 practical examples include the power law, the Pareto principle (more commonly known as the 80–20 rule), and product sales (i.e. best selling products vs others).
Markov Chains
A Markov chain is a mathematical system that experiences transitions from one state to another according to certain probabilistic rules. The defining characteristic of a Markov chain is that no matter how the process arrived at its present state, the possible future states are fixed. In other words, the probability of transitioning to any particular state is dependent solely on the current state and time elapsed.
Mean Imputation
Mean imputation is the practice of replacing null values in a data set with the mean of the data.
- Mean imputation is generally bad practice because it doesn’t take into account feature correlation. For example, imagine we have a table showing age and fitness score and imagine that an eighty-year-old has a missing fitness score. If we took the average fitness score from an age range of 15 to 80, then the eighty-year-old will appear to have a much higher fitness score that he actually should.
- Second, mean imputation reduces the variance of the data and increases bias in our data. This leads to a less accurate model and a narrower confidence interval due to a smaller variance.
Naive Bayes
One major drawback of Naive Bayes is that it holds a strong assumption in that the features are assumed to be uncorrelated with one another, which typically is never the case.
One way to improve such an algorithm that uses Naive Bayes is by decorrelating the features so that the assumption holds true.
Pros:
- Easy and fast.
- works for multi class prediction
- performs great when independence assumption holds true
- also performs well with bell curve assumption
Cons:
- Category in test data not mentioned in train data will result in 0 probalility.
- almost impossible to find data with no correlation
Neural Network
- A neural network is a multi-layered model inspired by the human brain. Like the neurons in our brain, the circles above represent a node.
- The blue circles represent the input layer, the black circles represent the hidden layers, and the green circles represent the output layer.
- Each node in the hidden layers represents a function that the inputs go through, ultimately leading to an output in the green circles. The formal term for these functions is called the sigmoid activation function.
What do you understand by the term Normal Distribution?
Data is distributed around a central value without any bias to the left or right and reaches normal distribution in the form of a bell-shaped curve.
The random variables are distributed in the form of a symmetrical, bell-shaped curve.
Properties of Normal Distribution are as follows;
- Unimodal -one mode
- Symmetrical -left and right halves are mirror images
- Bell-shaped -maximum height (mode) at the mean
- Mean, Mode, and Median are all located in the center
- Asymptotic
Infection rates at a hospital above a 1 infection per 100 person-days at risk are considered high. A hospital had 10 infections over the last 1787 person-days at risk. Give the p-value of the correct one-sided test of whether the hospital is below the standard.
Since we looking at the number of events (# of infections) occurring within a given timeframe, this is a Poisson distribution question.
The probability of observing k events in an interval
- *Null** (H0): 1 infection per person-days
- *Alternative** (H1): >1 infection per person-days
k (actual) = 10 infections
lambda (theoretical) = (1/100)*1787
p = 0.032372 or 3.2372% calculated using .poisson() in excel or ppois in R
Since p-value < alpha (assuming 5% level of significance), we reject the null and conclude that the hospital is below the standard.
Precision and Recall
Recall - proportion of actual positives was identified correctly
- Recall = TP/(TP+FN)
Precision - proportion of positive identifications was actually correct
- Precision = TP/(TP+FP)
An HIV test has a sensitivity of 99.7% and a specificity of 98.5%. A subject from a population of prevalence 0.1% receives a positive test result. What is the precision of the test (i.e the probability he is HIV positive)?
Precision = Positive Predictive Value = PV PV = (0.001\*0.997)/[(0.001\*0.997)+((1–0.001)\*(1–0.985))] PV = 0.0624 or 6.24%
You roll a biased coin (p(head)=0.8) five times. What’s the probability of getting three or more heads?
General Binomial Probability formula:
p = 0.8 n = 5 k = 3,4,5
P(3 or more heads) = P(3 heads) + P(4 heads) + P(5 heads) = 0.94 or 94%
Probability Fundamentals
Eight rules of probability:
- For any event A, 0 ≤ P(A) ≤ 1; in other words, the probability of an event can range from 0 to 1.
- The sum of the probabilities of all possible outcomes always equals 1.
- P(not A) = 1 — P(A); This rule explains the relationship between the probability of an event and its complement event. A complement event is one that includes all possible outcomes that aren’t in A.
- If A and B are disjoint events (mutually exclusive), then P(A or B) = P(A) + P(B); this is called the addition rule for disjoint events
- P(A or B) = P(A) + P(B) — P(A and B); this is called the general addition rule.
- If A and B are two independent events, then P(A and B) = P(A) * P(B); this is called the multiplication rule for independent events.
- The conditional probability of event B given event A is P(B|A) = P(A and B) / P(A)
- For any two events A and B, P(A and B) = P(A) * P(B|A); this is called the general multiplication rule
-
Factorial Formula: n! = n x (n -1) x (n — 2) x … x 2 x 1
Use when the number of items is equal to the number of places available.
Eg. Find the total number of ways 5 people can sit in 5 empty seats.
= 5 x 4 x 3 x 2 x 1 = 120 -
Fundamental Counting Principle (multiplication)
This method should be used when repetitions are allowed and the number of ways to fill an open place is not affected by previous fills.
Eg. There are 3 types of breakfasts, 4 types of lunches, and 5 types of desserts. The total number of combinations is = 5 x 4 x 3 = 60 -
Permutations: P(n,r)= n! / (n−r)!
This method is used when replacements are not allowed and order of item ranking matters.
Eg. A code has 4 digits in a particular order and the digits range from 0 to 9. How many permutations are there if one digit can only be used once?
P(n,r) = 10!/(10–4)! = (10x9x8x7x6x5x4x3x2x1)/(6x5x4x3x2x1) = 5040 -
Combinations Formula: C(n,r)=(n!)/[(n−r)!r!]
This is used when replacements are not allowed and the order in which items are ranked does not mater.
Eg. To win the lottery, you must select the 5 correct numbers in any order from 1 to 52. What is the number of possible combinations?
C(n,r) = 52! / (52–5)!5! = 2,598,960
Probability of A and/or B
Formulas:
- p(A and B) = p(A) * p(B) __ independent events
- p(A and B) = p(A) * p(B|A) __ dependent events
- p(A or B) = p(A) + p(B) __ mutually exclusive events
- p(A or B) = p(A) + p(B) - p(A and B) __ not mutually exclusive events
Given:
- P(A) = 0.6
- P(B) = 0.8
Therefore:
- P(A or B) = P(A) + P(B) — P(A and B)
- P(A or B) = 0.6 + 0.8 — (0.6*0.8)
- P(A or B) = 0.92
Explain how a ROC curve works?
The ROC curve is a graphical representation of the contrast between true positive rates and false-positive rates at various thresholds. It is often used as a proxy for the trade-off between the sensitivity(true positive rate) and false-positive rate.
How do you calculate the needed sample size?
You can use the margin of error (ME) formula to determine the desired sample size.
- t/z = t/z score used to calculate the confidence interval
- ME = the desired margin of error
- S = sample standard deviation
