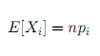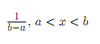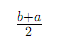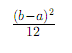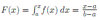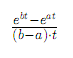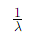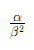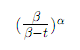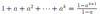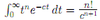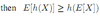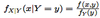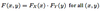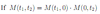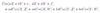Distributions P-1

Question 1

Discrete Uniform: Density Function

Answer 1

{1,2,3,…,N}

Question 2

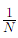
Discrete Uniform: Mean

{1,2,3,…,N}

Answer 2

Question 3

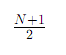
Discrete Uniform: Variance

{1,2,3,…,N}

Answer 3

Question 4

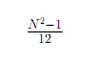
Discrete Uniform: MGF

Answer 4

Question 5

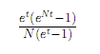
Binomial: Density

Answer 5

Out of n objects drawn, with probability of success p, x are successful.

Question 6

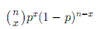
Binomial: Mean

Answer 6

Question 7

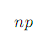
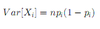
Binomial: Variance

Answer 7

Question 8

Binomial: MGF

Answer 8

Question 9

Geometric: Density

Answer 9

Probability of the first success on x-1 trials. Probability of success is p.

Question 10

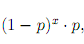
Geometric: Mean

Answer 10

The mean for the number of failures until the first success. The alternative, the trial of the first success. To find this add one to the expecation of failures and get 1/p.

Question 11

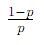
Geometric: Variance

Answer 11

Question 12

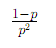
Geometric: MGF

Answer 12

Question 13

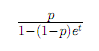
Poisson: Density

Answer 13

Probability of x occurances over a unit of time. Lambda is the average rate of occurance.

Question 14

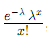
Poisson: Variance and Mean

Answer 14

Question 15

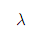
Poisson: MGF

Answer 15

Question 16

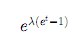
Negative Binomial: Density

Answer 16

Repeat and experiment with success probability p until the rth success. x is the number of failures until the rth success.

Question 17

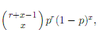
Negative Binomial: Mean

Answer 17

Question 18

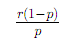
Negative Binomial: Variance

Answer 18

Question 19

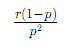
Negative Binomial: MGF

Answer 19

Question 20

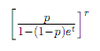
Hypergeometric: Density

Answer 20

In a group of M objects, K are type one objects. M-K are type two. n is the number of objects drawn and x is the number of type one objects drawn.

Question 21

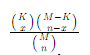
Hypergeometric: Mean

Answer 21

Question 22

Hypergeometric: Variance

Answer 22

Question 23

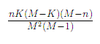
Multinomial: Density

Answer 23

Out of n trials, x_i are from group i and have probability p_i.

Question 24

Multinomial: Mean i

Answer 24

Question 25

Multinomial: Variance i

Answer 25

Question 26

Continuous Uniform: Density

Answer 26

An interval from a to b.

Question 27

Continuous Uniform: Mean

Answer 27

Question 28

Continuous Uniform: Variance

Answer 28

Question 29

Continuous Uniform: Cumulative

Answer 29

Question 30

Continuous Uniform: MGF

Answer 30

Question 31

Exponential: Density

Answer 31

Question 32

Exponential: Mean

Answer 32

Question 33

Exponential: Variance

Answer 33

Question 34

Exponential: MGF

Answer 34

Question 35

Exponential: Cumulative

Answer 35

Question 36

Normal: Density

Answer 36

Question 37

Normal: MGF

Answer 37

Question 38

Gamma: Density

Answer 38

Question 39

Gamma: Mean

Answer 39

Question 40

Gamma: Variance

Answer 40

Question 41

Gamma: MGF

Answer 41

Question 42

What is a sum of a geometric?

Answer 42

Question 43

The integral of a quadratic and natural exponential.

Answer 43

Question 44

Taylor Expansion of e^x.

Answer 44

Question 45

The Order Statistic equation.

Answer 45

Max is k = n and min is k = 1.

Question 46

Using a cdf to find the intersection.

Answer 46

Question 47

Chebyshev's Inequality

Answer 47

Question 48

A common exponential integral.

Answer 48

Question 49

Convolution 1. When to use it. 2. Its two forms. 3. What the equation solves. 4. Those two equations.

Answer 49

Question 50

Union through a joint cdf.

Answer 50

Question 51

Transformation pdf.

Answer 51

Question 52

Transformation cdf.

Answer 52

Question 53

A linear transformations affect on the MGF.

Answer 53

Question 54

Jensen's Inequality

Answer 54

Question 55

Grand Variance through condinitional variances.

Answer 55

Question 56

Continuous conditional equation.

Answer 56

Question 57

Correlation coefficient.

Answer 57

Question 58

Independence and the joint cdf.

Answer 58

Question 59

Independence and expectations.

Answer 59

Question 60

Independence and joint MGF.

Answer 60

Question 61

Independence and joint pdf.

Answer 61

Question 62

The covariance of two linear equations.

Answer 62

Question 63

The multiplication rule for the joint.

Answer 63