Distributions

Question 1

Uniform Distribution

Answer 1

Question 2

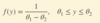
Uniform distribution: Mean

Answer 2

µ = (ø₁ - ø₂) / 2

Question 3

Uniform Distribution: Variance

Answer 3

V(Y) = (ø₂ = ø₁)² / 12

Question 4

Normal Distribution

Answer 4

Question 5

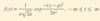
E(Y), Y ≈ N

Answer 5

E(Y) = µ

Question 6

V(Y), Y ≈ N

Answer 6

V(Y) = σ²

Question 7

Standard normal random variable, Z

Answer 7

Z = (Y - µ)/σ

Question 8

Gamma distribution function

Answer 8

Question 9

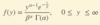
Gamma Function

Answer 9

Question 10

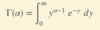
E(Y), Y ≈ Gamma(α, β)

Answer 10

E(Y) = αβ

Question 11

V(Y), Y ≈ Gamma(α, β)

Answer 11

V(Y) = αβ²

Question 12

Chi-Square distribution function with v degrees of freedom.

Answer 12

A gamma-distributed random variable with parameters:

α = ^v/₂,

β = 2

Question 13

E(Y), Y ≈ χ²

Answer 13

E(Y) = β

Question 14

V(Y), Y ≈ χ²

Answer 14

V(Y) = β²

Question 15

Exponential Distribution

Answer 15

Question 16

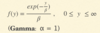
E(Y), Y ≈ Exp(y, β)

Answer 16

E(Y) = β

Question 17

V(Y), Y ≈ Exp(y, β)

Answer 17

V(Y) = β²

Question 18

Beta Function

Answer 18

Question 19

Beta Distribution Function

Answer 19

Question 20

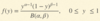
E(Y), Y ≈ Beta(α, β)

Answer 20

E(Y) = ^α/_{(α + β)}

Question 21

V(Y), Y ≈ Beta(α, β)

Answer 21

V(Y) = ^αβ/_{(α + β)²(α + β + 1)}

Question 22

Cov(Y₁, Y₂)

Answer 22

E[(Y₁ - µ₁)(Y₂ - µ₂)]

Question 23

Properties of a Distribution Function

Answer 23

1. F(-∞) = 0
2. F(∞) = 1
3. F(y) is a nondecreasing function of y.

Question 24

Properties of a density function

Answer 24

1. f(y) ≥ for all y, -∞ < y < ∞
2. Int _-∞^∞ f(y) dy = 1