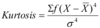Descriptive Statistics

Question 1

Measures of Central Tendency:

Measures of Dispersion:

Measures of Shape

Answer 1

A single value that summarises a set of data. It locates the central value of a set of data.

Measures the variation around the central value of a data set.

The shape of the distribution.

Question 2

Properties of the mean

Answer 2

The sum of the deviations of each value from the mean will always be zero The arithmetic mean is the only measure of location where the sum of the deviations of each value from the mean will always equal zero.

Question 3

Median

Answer 3

•Where:

–L is the lower limit of the class containing the median.

–n is the total number of frequencies.

–f is the frequency in the median class.

–CF is the cumulative number of frequencies in all the classes preceding the class containing the median.

–i is the width of the class in which the median lies.

Question 4

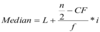
Mode

Answer 4

L is the lower limit of the class containing the mode.

f1 is the frequency of the mode class.

f2 is the frequency of the previous class to the mode class.

f3 is the frequency of the next class to the mode class.

i is the width of the class in which the mode lies.

Question 5

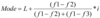
Disadvantages of the
Mode

Answer 5

In many sets of data, there is no mode because no value appears more than once.

Some data sets have more than one mode.

Question 6

•Measures of dispersion include:

Answer 6

–Range

–Variance

–Standard Deviation

Question 7

Measures of Dispersion

Answer 7

• A small value for a measure of dispersion indicates that the data are clustered closely around the mean. A mean is therefore considered representative of the data.
• A large measure of dispersion indicates that the data are spread from the mean. A large measure of dispersion indicates the mean is not reliable.

Question 8

Variance/Standard Deviation

Answer 8

• Low variance/standard deviation suggest that most of our observations are clustered around the mean value.
• High variance/standard deviation suggest that observations are more spread out.

Question 9

Descriptive Statistics

Answer 9

•Measures of Central Tendency:

–A single value that summarises a set of data. It locates the central value of a set of data.

–Mean, Median, Mode

•Measures of Dispersion:

–Measures the variation around the central value of a data set.

–Range, Variance, Standard Deviation

•Measures of Shape

–The shape of the distribution.

–Skewness, Kurtosis

Question 10

Skewness

Answer 10

• In a positively skewed distribution, the mean is the largest of the three averages.
• If one or more observations are extremely large, the mean of the distribution becomes greater than the median or mode.
• The median is generally the next largest average in a positively skewed distribution after the mean.
• The mode is the smallest of the three averages

Question 11

Positively skewed

Answer 11

Positively- Skewed

Tail to the Right

Mean > Median > Mode

Question 12

Negatively skewed

Answer 12

• In a distribution that is negatively skewed, the mean is the lowest of the three averages.
• The mean is influenced by a few extremely low observations.
• The median is greater than the mean.
• The mode is the largest of the three averages.

Question 13

Skewness is calculated using Pearson’s coefficient of skewness.

Skewness is calculated as follows:

Answer 13

Question 14

Kurtosis

Answer 14

Kurtosis is the degree of peakedness of a distribution. It is a measure of shape.

These graphs show the notion of kurtosis. The graph on the right has a higher kurtosis than the graph on the left. It is more peaked at the center, and it has fatter tails. (more observations in the higher and lower ends of the distribution)

Question 15

Kurtosis formula & result meaning

Answer 15

•If the calculated value for kurtosis is equal to 3 it is said to be mesokurtic

•

•If the calculated value is less than 3 it is said to be platykurtic

•

•If the calculated value is greater than 3 it is said to be leptokurtic