derivatives

Question 1

definition of the derivative

Answer 1

Question 2

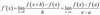
power rule

Answer 2

Question 3

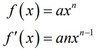
derivative of exponential function (including simple case)

Answer 3

Question 4

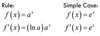
derivative of logarithmic function

Answer 4

Question 5

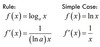
derivative of sin(ax)

Answer 5

Question 6

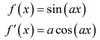
derivative of cos (ax)

Answer 6

Question 7

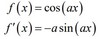
derivative of tan(ax)

Answer 7

Question 8

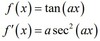
derivative of csc(ax)

Answer 8

Question 9

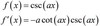
derivative of sec(ax)

Answer 9

Question 10

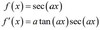
derivative of cot(ax)

Answer 10

Question 11

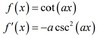
derivative of arcsin(ax)

Answer 11

Question 12

derivative of arccos(ax)

Answer 12

Question 13

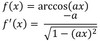
derivative of arctan(ax)

Answer 13

Question 14

derivative of [f(x)^g(x)]

Answer 14

Question 15

critical point definition

Answer 15

critical point = a point (c) in the domain of f at which

f’(c) = 0, or

f’(c) is undefined

Question 16

significance of the sign of f’(x)

Answer 16

if f’(x) > 0 (positive), the function is increasing on the given interval

if f’(x) < 0 (negative), the function is decreasing on the given interval

Question 17

inflection point (definition)

Answer 17

inflection point = a point on the graph where it changes from concave up to concave down

Question 18

relationship btwn inflection points and critical points

Answer 18

all inflection points are critical points, but not all critical points are inflection points

Question 19

significance of the sign of f’‘(x)

Answer 19

if f’‘(x) > 0 (positive), the function is concave up on the given interval

if f’‘(x) < 0 (negative), the function is concave down on the given interval

Question 20

chain rule

Answer 20

Question 21

product rule

Answer 21

Question 22

quotient rule

Answer 22

Question 23

algorithm for implicit differentiation

Answer 23

Question 24

algorithm for logarithmic differentiation

Answer 24

Question 25

l'Hopital's rule

Answer 25

Question 26

indeterminate forms that can't be solved using l'hopital (product, difference, exponential)

Answer 26