Deck 1 Flashcards
Prime numbers below 60
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59
An isosceles right triangle (45-45-90)
has sides in a ratio of x : x : x√2
A 30-60-90 triangle
has sides in a ratio of x : x√3 : 2x
To count # of factors of positive N integer
- Find prime factorization of # 2. Make list of exponents of the prime numbers 3. Add 1 to every # on the list 4. Multiply all those #s together
To find GCF
- Find prime factorization of both #s 2. What are the highest powers they have in common? 3. Multiply the highest powers to get GCF
To find LCM
- Take the prime factorization of each #, 2. Find what prime factors appear in both, 3. Multiply one of each of the shared primes and then by all the unshared primes
Divisible by 3
sum of digits divisible by 3
Divisible by 4
the last 2 digits of number are divisible by 4
Divisible by 5
the last digit is either a 5 or 0
Divisible by 6
even number and sum of digits is divisible by 3
Divisible by 8
if the last 3 digits are divisible by 8
Divisible by 9
sum of digits is divisible by 9
Percent change
(change/original value) * 100





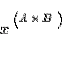
1 raised to any power is
1
0 raised to any nonzero power is
0
Any nonzero number to the power of 0 is
1





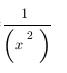






Factoring using quadratic polynomials

(x+m)(x+n) where a is the sum of m and n and b is their product


If 2 lines intersect, the sum of the resulting 4 angles equals
360
Total degrees of a polygon (a figure with 3 or more sides) =
180 (n-2), where n = # of sides
Area of a triangle
1/2 b x h
Pythagorean triplets
- 3-4-5
- 5-12-13
- 8-15-17
- 7-24-25
Area of a circle

Circumference of a circle

How many degrees in a circle
360
Arc Length

Arc
portion of the circumference of a circle in x degrees of the circle
Area of a sector

chord
line segment between two points on a circle
if 2 inscribed angles of a circle hold the same chord…
the two inscribed angles are equal
an inscribed angle holding the diameter is…
a right angle
inscribed angles holding chords/arcs of equal length…
are equal
Area of a square
side^2
Area of a rectangle
length x width
Area of a trapezoid

Area of a parallelogram
base x height, where the base forms a right angle with the height
Volume of cube
side^3
Surface area of cube
6s^2
Volume of rectangular solids (including cubes)
height x depth x width
Surface area of rectangular solids (including cubes)
total of the areas of each rectangle
Volume of a cylinder

Surface Area of a Cylinder

Slope of a line

Slope of two lines that are perpendiular to each other
negative reciprocal
Distance formula (to find the distance between two points)

Graph of a quadratic equation
in a parabola
Quadratic equation
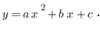
Distance formula
Distance = Rate x Time
Work Rate Formula
Output = rate x time
Sum of consecutive integers from 1 to n

Simple interest

Compound interest

Fundamental Counting Principle
If a task is comprised of stages, where…
One stage can be accomplished in A ways
Another can be accomplished in B ways
Another can be accomplished in C ways
…and so on, then the total number of ways to accomplish the task is A x B x C x …
Factorial notation

Combinations
When order does not matter

Permutations
When order does matter

Probability that event A will happen

The complement of an event
The chance the event doesn’t occur (e.g., the complement of drawing a green ball is drawing a ball that isn’t green)
If A and B are independent events, P (A and B) =
P (A) x P (B)
P (A or B) =
P (A) + P (B) - P (A and B)
If A and B are dependent events, P (A and B) =

The Triangle Inequality
The sum of any two sides of a triangle must be bigger than the third side
Number of integers from m to n inculsive
n-m+1
“per capita”
per person
1 million
1,000,000
1 billion
1,000,000,000
Adding inequalities vertically can only be done if…
…the signs face the same direction
mean and median in an evenly spaced set
In an evenly spaced set, the median is always equal to the mean
To find the middle number of an evenly spaced set
take the average of two extremes
Inscribed figure
One that is drawn inside another with only the sides touching

Arithmetic sequence
- same number is added to each element to get the next element
- mean = median
(x-y) / (y-x) =
= -1
Area of an equilateral triangle

weighted average formula
weighted average = sum (percent weight *number)
Surface area of a cube
6(side length)^2
Volume of a cube
(side length)^3
Recall that the remainder, in any division problem:
Recall that the remainder, in any division problem, must be less than the divisor (the number by which you divide).
A diagonal in a rectangle
A diagonal divides a rectangle into two equal triangles
Any fraction between 0 and 1 multiplied by itself will what in value?
Any fraction between 0 and 1 multiplied by itself will decrease in value
whenever the numbers in the set are equally spaced =
whenever the numbers in the set are equally spaced:
- the mean (average) is equal to the median (the middle number)
- the overall average is equal to the average of the first and last terms
Exterior Angle Rule
Exterior Angle Rule states that the measure of an exterior angle is equal to the sum of the measures of the two “remote” interior angles, i.e., the interior angles that do not border the exterior angle in question.
Distance between points



